以一见多 高效教学
●杨苍洲 (惠安县高级中学 福建泉州 362100)
“倡导积极主动、勇于探索的学习方式”是《普通高中数学课程标准》(以下简称《新课程标准》)的理念之一.《新课程标准》指出:学生的数学学习活动不应只限于接受、记忆、模仿和练习,高中数学课程还应倡导自主探索、动手实践、合作交流、阅读自学等学习数学的方式.因此,在高中数学课堂中,笔者倡导“以一见多,高效教学”.这里的“一”是指为学生构造共同基础,提供发展平台,“多”是指注重提高学生的数学思维能力和发展学生的数学应用意识,从而实现高效教学.下面笔者就几个教学案例谈谈如何应用“以一见多”的教学方法实现高效教学.
1 一题多解,培养学生的发散性思维
“一题多解”要求学生学会对所给的材料、信息从不同角度、往不同方向、用不同方法或途径进行分析和解决问题,从而培养学生的发散思维能力.它可以通过纵横发散,使知识串联、综合沟通,达到举一反三的目的,同时能有效激发学生探索求新的欲望,提高学习数学的兴趣.
案例1 已知x2+y2=1,求z=3x+4y的取值范围.
该案例是笔者在讲授人教版高中数学选修4-5“不等式选讲”中采用的一个例子.因为当时介绍的是“柯西不等式”的相关内容,所以课堂上师生利用“柯西不等式”共同完成了不等式的证明.
解法1 利用柯西不等式.由
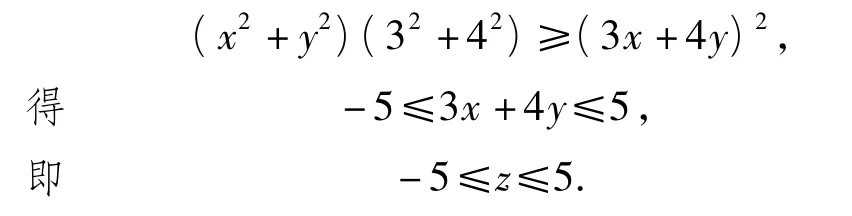
解法2 利用柯西不等式.由
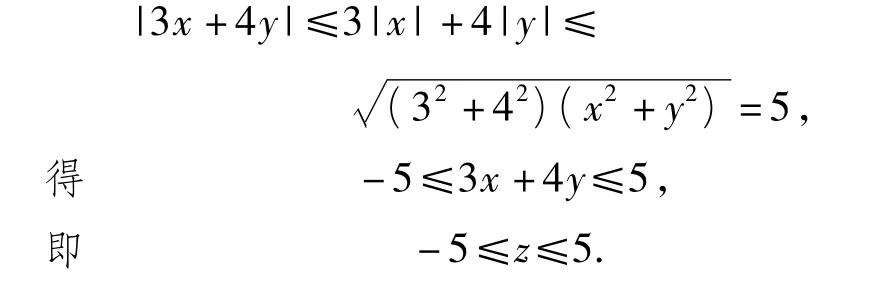
至此,该例题已经完成它作为复习巩固“柯西不等式”的任务,但为了充分发挥例题的教学功能,培养学生的发散思维能力,提高学生的综合解题能力,笔者引导学生继续探究新的解题方法.经过师生的共同努力得到以下几种解法:
解法3 利用线性规划.
如图1所示,首先作直线 l0:3x+4y=0,然后平移l0至位置l1,易得l1的纵截距为,故 z=5.同理,平max移l0至位置l2,易得l2的纵截距为-,故 zmin=-5.
综上所述,-5≤z≤5.
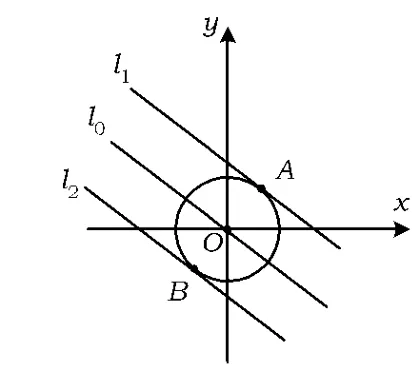
图1
解法4 利用判别式.
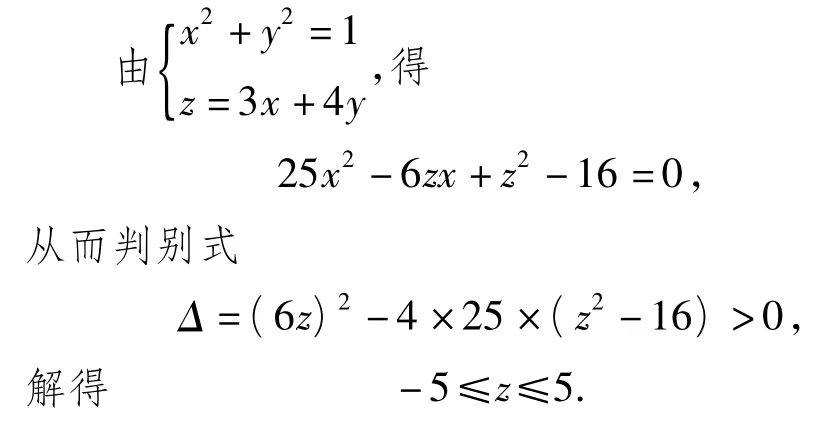
解法5 利用参数.
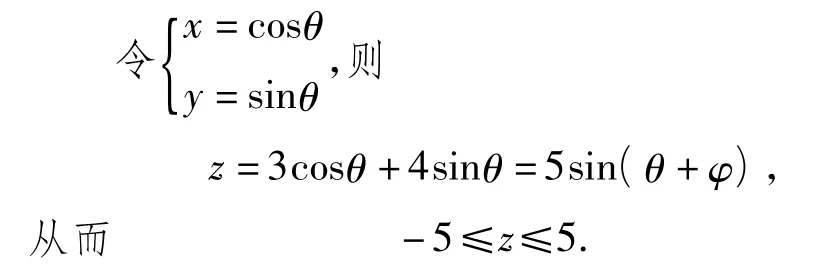
解法6 利用向量法.
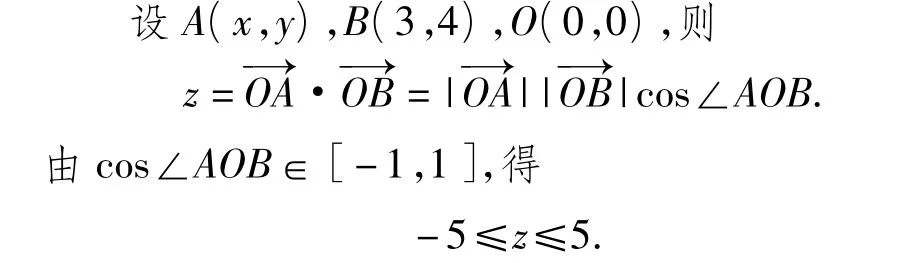
上述几种解法复习了线性规划求最值、判别式法求最值、圆的参数方程、向量的数量积等高中数学的主干知识,同时也涉及到函数方程、数形结合、转化化归等重要的数学思想方法,正可谓“以小见大,一举多得”.因此,在教学预设中,若能选择适当的例题,并引导学生进行多角度的思考与探索,则可实现知识与技能、思想与方法等各方面数学基本功的复习与巩固、融合与交汇.
2 一法多题,培养学生的收敛性思维
“一法多题”要求学生学会将含某一知识点的习题进行分类整合,归纳出其共同的解题方法和技巧,从而培养学生的收敛性思维和综合归纳能力.它通过对知识的梳理、归纳、提炼,并在异中求同,从而揭开不同问题的表面现象,挖掘出知识的本质结构,掌握知识的规律性,从而使学生脱离题海,获得事半功倍的效果.
案例2 设抛物线y2=4x,过点P(2,0)的直线 l交抛物线于点A(x1,y1),B(x2,y2),求 AB 中点Q的轨迹.
该例题是笔者在复习“直线与圆锥曲线位置关系”时采用的一个例子,问题牵涉到直线与圆锥曲线相交弦的中点问题,可以采用设而不解的方法,用韦达定理进行求解.在平时的练习中,经常会遇到此类问题,为彻底解决此类问题,笔者布置给学生一个课外作业,要求学生对该例题进行适当的变式,总结归纳并编拟出几种常见例题.实践证明,学生的创造能力远远超出教师的想象,笔者摘录了部分学生编拟的典型例题.
例1 设抛物线y2=4x,过点P(2,0)的直线l交抛物线于点 A(x1,y1),B(x2,y2),求△AOB 重心G的轨迹.
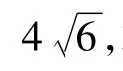
例3 设抛物线y2=4x,过点P(2,0)的直线l交抛物线于点 A(x1,y1),B(x2,y2).若 S△AOB=8,求此时直线AB的方程.
例4 设抛物线y2=4x,过点P(2,0)的直线l交抛物线于点 A(x1,y1),B(x2,y2),证明△AOB 是钝角三角形.
案例2以及例题1~5都是直线与圆锥曲线相交弦的问题,牵涉到中点、三角形重心、弦长、三角形面积、向量内积、向量共线等问题.这些问题都可以采用设而不解的方法,用韦达定理进行求解,其解题程序基本一致,因此可以对它们进行归纳总结,实现适度的形式化.笔者建议,在解完一道典型例题后,教师要引导学生通过联想、拓展和深究,举一反三,并适时地将解题经验实现发散性和收敛性迁移,以进一步扩大“战果”,从而获得较熟练的解题技能.因此,通过引导学生进行例题的归纳总结,可实现“一法多题”教学,从而提高课堂的教学效率和学生的学习效率.
3 一题多得,培养学生的创造性思维
“一题多得”要求学生能对问题进行类比迁移、归纳推广,能提出个人的猜想,并证明或否定,从而得到新的问题、新的结论.它通过一个问题的教学过程,形成“问题蘑菇群”,从而唤起学生的问题意识.问题意识是创新的基石,是培养创新精神的起点,也是培养创新人才的有效方法.因此在教学中,应用“一题多得”的教学方法,能有效锻炼学生的类比思维、求异思维和创造性思维能力.
(1)求椭圆C的方程.
(2)E,F是椭圆C上的2个动点.如果直线AE的斜率与AF的斜率互为相反数,证明直线EF的斜率为定值,并求出这个定值.
(2009年辽宁省数学高考理科试题)
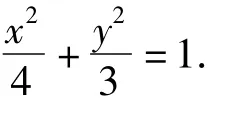
(证明略.)
该题是笔者在授课中所采用的一个例题,讲解完毕后,笔者发现:点A的横坐标恰与椭圆右焦点的横坐标相同,直线EF的斜率恰为椭圆的离心率e.那么是否所有的椭圆都有上述性质呢?笔者建议对此问题进行推广探究,得到以下命题.
考虑将椭圆一般化,有:
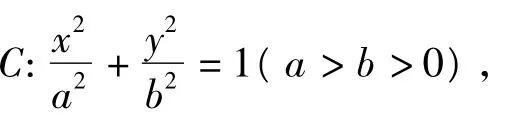
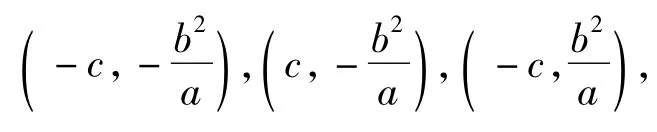
椭圆具有上述性质,在圆锥曲线内进行平行类比,在双曲线中是不是也有相同的性质?于是笔者引导学生继续探究,得:
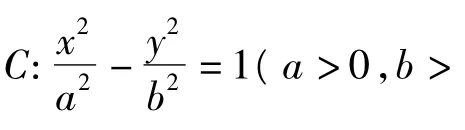
椭圆和双曲线都称之为有心圆锥曲线,它们具有极为相似的性质.但是,它们所共有的性质不一定能类比推广到抛物线,那么在抛物线中是不是也有上述性质呢?回答是肯定的.
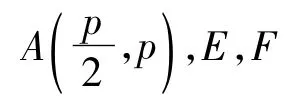
从命题1~3可归纳出圆锥曲线所共有的一个优美性质:
命题4 已知A是圆锥曲线C上一个定点,E,F是圆锥曲线C上的2个动点.若点A与曲线一个焦点的连线垂直于对称轴,且 kAE+kAF=0,则|kEF|=e.
完成了从椭圆到双曲线、抛物线的类比,本应结束探究,但为了使学生对圆锥曲线问题有更进一步的理解,笔者引导学生课后进行再探究:当点A为曲线上任意一定点,是否还能得到如此优美的性质?继续探究可得:
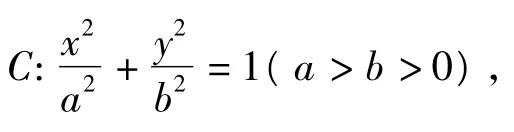
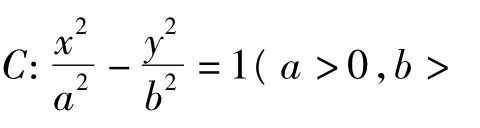
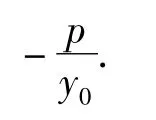
探究没有停止,接着引导学生尝试把点A移到曲线外,得到:
命题8 已知M,N,P,Q为圆锥曲线C上不同的4个点.若 kMN+kPQ=0,则 kMQ+kPN=0,kMP+kNQ=0.
教育家波利亚曾说:“学习任何知识的主要途径即是由自己去发现,因为这一发现,理解最深刻、也最容易掌握其中的内在规律、性质和联系.”随着课程教学改革的深入开展,在实施素质教育的今天,要培养学生的创新意识和实践能力,其中一条很重要的途径就是让学生在数学学习中经历知识的探索过程.也只有在这个过程中,学生才会有体验、有发展,也就是说要变原来的“听数学”、“学数学”为“做数学”,让学生在做中学,在做中获得不断发展.
[1] 杨苍洲,陈一平.设而不解 事半功倍[J].数学教学通讯,2009(35):34-35.

