善用数学课堂错误 促进学生认知发展
●赵向阳 (陶朱初中 浙江诸暨 311800)
“错误”是指师生在认知过程中的偏差或失误.在常规的数学课堂教学中,学生出错是常见的现象,许多教师对此头疼不已.事实上,学生出错是正常现象,新课标在情感与态度的目标中明确提出:学生要能在他人的指导下,能够发现数学活动中的错误并及时改正.在学生的学习过程中,“正确,有可能是一种模仿;错误,却大凡是一种经历”.学生的数学知识与能力水平在正确与错误的交错下提升与发展,错误与正确是每个学生成长过程中必经的阶梯.因此,教师应当正视错误,善用错误资源,借力于“错误”提高课堂教学的有效性,化“腐朽”为“神奇”.
1 预设错误,引发学生认知冲突
课堂上的错误,有些是教师能够预料到的.教师通过认真钻研教材,研究学情,凭借教学经验,发现学生发生错误的规律,预设学生学习认知过程中可能发生的错误.教学不仅仅是单向地组织学生学习正确的知识,更重要的是让学生在正确与错误之间不断碰撞、思索、讨论,从而展现多姿多彩、充满挑战的课堂.
1.1 预设错误,引入新知
弗赖登塔儿认为,数学学习是基于学生数学现实的数学化过程.一线教师普遍认为数学现实是学生已掌握的数学知识与相关的数学现实背景.实际上,数学现实也包括一些未能完全掌握的数学知识,数学的再创造也是可以以不正确的认知为出发点的.教师通过预设错误,引发认知冲突,从而导入新知.这样,学生更有学习兴趣,同时更容易留下深刻印象.
案例1 八年级数学上册“直角三角形全等的判定”引入.
课始,投影展示一道几何证明题过程如下:
例1 在△ACB和△A'C'B'中,∠C=∠C'=90°,AB=A'B',AC=A'C',求 证:△ACB ≌△A'C'B'.
证明在△ACB和△A'C'B'中,因为
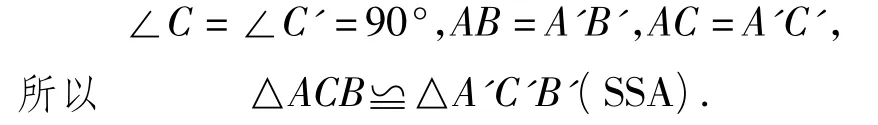
问题 请学生谈谈对这一道例题及证明过程的看法.
一部分学生很快发现证明过程中全等判定方法应用出错,错在SSA不是普通三角形的全等判定方法,并及时回顾全等三角形的判定方法.进一步提问:SSA判定普通三角形全等为什么不行?进而引导学生发现命题为真命题,引出直角三角形全等的判定方法,并探究这一命题的证明方法.
1.2 预设错误,辨析新知
对新知的认识,要从正、反面去理解.在新概念或新性质学习之后,利用预设的错误现象,引导学生在辨析中更加完整、全面地认知新知识,是学习新知识常用的方法.这种预设的错误有时来自教师提供的材料,但缺少亲和力,教师应尽可能从学生问题解决过程中撷取看似随意产生、实际上是预设的一些错误以供辨析.因为这些错误就发生在学生身边,所以更有真实感与冲击力.
案例2 七年级数学上册“数轴概念”辨析.
师生共同合作将温度计抽象成数轴并定义数轴,让每个学生动手画一条数轴,并与同桌交换自己所画的图形,交流所画的数轴是否完整,如果不完整或不正确,记录错误并加以完善.达成共识后,请学生汇报作图过程中的一些错误(如图1),师生共同归纳画数轴的注意点,强调数轴的三要素缺一不可.
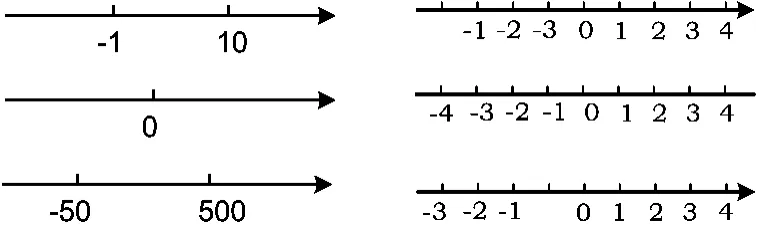
图1
1.3 预设错误,巩固新知
在数学应用过程中,不同层次的问题,反映不同层次的应用水平,也反映学生新知掌握的不同程度.教材中的例题通常是针对大众化的学生设计,面对真实有鲜活个性的学生,课堂教学往往会做适当的变化,一方面进行开放训练或是探究数学应用,另一方面通过更高要求的变式问题发现学生中存在的问题.教师结合教学经验和学生的认知水平,可以在教学中创设一些变式问题,挖掘出学生认知的局限性,进而更好地完善新知应用能力.
案例3 九年级数学上册“圆的轴对称性”的例题变式.
例2 已知(如图2),用直尺和圆规作这条弧的中点.
变式用直尺和圆规求作的四等分点.
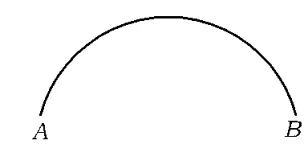
图2
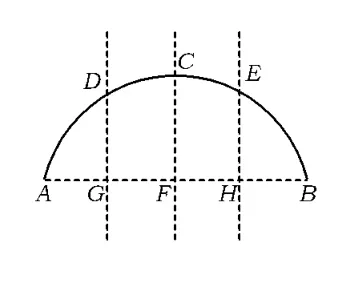
图3
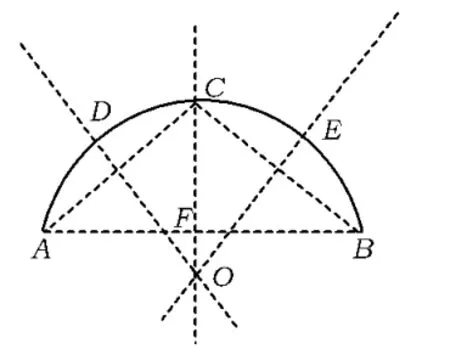
图4
2 捕捉错误,疏通学生认知盲点
许多学生课内外错误的产生具有随机性,这些错误有些是可利用的认知错误,有些则是无价值的.对于极具教学价值的错误,教师要及时捕捉并遴选,加以合理利用,为高效的课堂增添色彩.
2.1 捕捉错误,开拓思路
正确的方法,可能就在错误的认识隔壁.发现错误、分析错误后,或溯源而上或背道而行,可能得到正确的思路.因此,在教学过程中,可以捕捉与解题相关的错误信息,或逆推或反向或发散分析,也是开拓思路的好方法.
案例4 中考模拟题讲评:直角三角形面积平分.
例3 用12根相同的火柴棒首尾顺次相接,搭成一个三角形(如图5).若要平分这个三角形的面积,则至少还需要同样的火柴棒 ( )
A.1根 B.2根 C.3根 D.4根
一次初三模拟考中有一道题来源于小学的数学智慧题,以考查学生的数学应用能力.大部分学生选择C,理由是斜边上的中线可以将面积平分,但中线长为2.5根火柴,故选C.而个别选择正确答案B的学生反馈,也是根据2.5根猜答案不可能那么简单,故猜B.在试卷讲评课时,发现一部分学生不知道自己的答案是否正确,一部分学生知道自己的答案错误但不明白错误发生在哪里.学生的思维局限在分割后的图形仍然为三角形,故有2.5根的结论,点破后,学生的思维就打开了,通过尝试发现了2种分割方法(如图6).
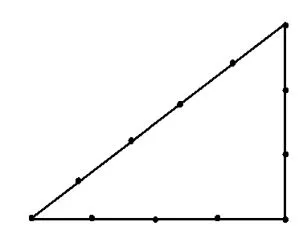
图5
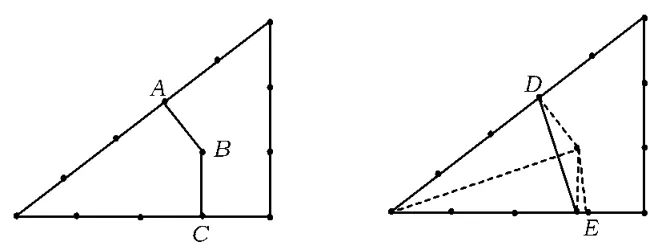
图6
2.2 捕捉错误,探索创新
正确的思维是解决问题的成功途径,那么错误的思维是否是解决问题时的失败途径呢?回答是否定的,一个错误的方法,也是基于相关的数学现象而产生的,只不过这个方法尚未完善,它可能是另一种问题解决的方法.错误也是成功的必经之路,甚至是创新的起点.
案例5 形如ax2=bx(a≠0)一元二次方程的特殊解法.
例4 解方程3x2=x.
一位学生在解此方程时,2边同除以x得3x=1,从而 x=.教师没有批评学生,而是引导学生与正确解法进行比较,比较正解与错解的不同之处,分析错解中漏解的原因是方程2边同除以x时,忽略了x=0所造成的.找出问题所在后,教师就势提出一问:你能将错解补充成正确的解答吗?学生在略微思考后,提出自己一个特殊解法:分类讨论法.当x=0时,是方程的解,当x≠0时,解得x=,所以原方程的解为x=0,x=.经过认真
12
思考,这位学生的解法得到了大家的认同,并在此基础上,总结出形如ax2=bx(a≠0)的一元二次方程的特殊解法:分类讨论法.
2.3 捕捉错误,及时纠正
不是所有错误都有利用价值,也不是所有错误都可以引发新方法与新思路.大部分错误的产生是因为学生的认知存在盲点,及时捕捉这些错误,共同解决,有利于学生及时清理知识盲区,从而实现高效课堂教学.
案例6 七年级数学上册“用字母表示数”引例.
引例 一只青蛙一张嘴,二只眼睛四条腿,扑通一声跳下水;二只青蛙二张嘴,四只眼睛八条腿,扑通扑通跳下水……
问题1 如果有更多数量的青蛙,那么这首儿歌该怎么唱?
问题2 如果青蛙的数量用字母n表示,那么这首儿歌又该怎么唱?
这个引例用了很多年,在初中数学课堂中基本都能顺利地引入新课.有一次,与一位小学教师同课异构时出现了意外,一个小学生答“n只青蛙n张嘴,n只眼睛n条腿”,在座的学生中还有不少支持者.在这些学生的认知中,n是代表说不清、数不完的数,有些学生在网络语言表达中会用“n多”.因此青蛙太多,数不清,用n代替,嘴太多,也是数不清,故也是用n代替,以此类推.此类错误不可马虎,要及时捕捉,引导学生发现错误所在.当时笔者就引导学生将n取2代入得到“2只青蛙2张嘴,2只眼睛2条腿”,这显然与前面事实相矛盾,并及时引导学生发现n并不是代表数不清的数,而是一个具体数量的代替.而青蛙、嘴、眼睛、腿之间存在着数量联系,在字母表示数时,这种数量关系要通过代数式表示出来,学生在错误分析“n只青蛙n张嘴,n只眼睛n条腿”的基础上及时纠错得到“n只青蛙2n张嘴,2n只眼睛4n条腿……”.
3 反思错误,完善学生认知结构
错误是始终伴随着学生学习过程的,学生在不断纠正错误的过程中,应当学会处理错误更高层次的方法——反思错误.反思是一种主动“再认识”的过程,是思维的高级形式.培养学生的反思习惯,有助于学生更好的学习,但初中阶段的学生毕竟在自控力方面有限,自主反思的习惯不易建立,往往需要一些方法督促其反思.
3.1 集错
集错,是广大数学教师熟悉的引导学生整理学习的方法.事实证明,这是一个行之有效的方法.集错本常用于收集作业或试卷中的错题,侧重在解题错误的整理,平时可以要求学生在问题边空白处简单注明错误的原因,学生用于复习查看效果较好.当然教师也应适当地整理学生的作业错误,积累经验,为以后的复习或下一轮的教学提供参考.
3.2 记错(日记)
每天选取课堂或课外的典型错误,不拘于作业或试卷,也可以是课堂学习中未明白的知识点等,并加反思,形成日记,有利于学生对错误进一步认识,也可以加深对正确认识的巩固.记错,应当有问题,有解决方案,有反思的完整错误认识过程,也是自身元认知水平发展的体现.
3.3 评错
在反思错误过程中,要学会对错误进行合理的评价,对错误的产生要有合理对待的态度.产生错误是正常现象,纠正错误是自身的一种成长,而由错误引发创新思维就是一种自身成长的突破.学生不仅要对自身错误有公正的评价,同时对其他学生所产生的错误也应该有正确的评价.因此,正确评价错误,也是学习水平发展的代表.
追求高效的课堂教学,体现数学教学价值,是每一个数学教师的目标.我们应当重视课堂“意外”,关注学生的“错误”.“意外”、“错误”的应对,需要一定的教学智慧,这是教师多种教育能力的结合,需要我们在日常教学中做有心人,时刻留意学生的所思所想,关注学生的知识生成,当然也包括学生的错误生成,积极研究学生的错误,只有这样才能取得更好的教学效果.

