基于神经网络的接触式测头半径三维补偿
张 伟,赵云飞
ZHANG Wei, ZHAO Yun-fei
(中国计量学院 机电工程学院,杭州 310018)
0 引言
零件的数字化是通过特定的测量设备和测量方法获取零件表面离散点的几何坐标数据,在这基础上进行复杂曲面的建模、评价、改进和制造。因此,高效、高精度地实现零件表面的数据采集是逆向工程实现的基础和关键技术之一[1]。零件表面数据采集方法可分为接触式数据采集和非接触式数据采集两大类。
三坐标测量机(CMM)是应用最为广泛的接触式测量设备,它具有噪声低、精度高和重复性好等优点。接触式测量包括点位触发式数据采集和连续式数据采集两种。点位触发式数据采集的速度较低,一般只适合零件表面形状检测或需要较少的表面数字化场合;连续式数据采集的速度较快,可用于采集较大规模的数据。接触式测量方法不足之处是对由较软材料制造的零件产生测量误差,测头半径需进行补偿。
接触式和非接触式测量方法各有优缺点,因此一些研究者应用多传感器信息融合的思想开发集成测量系统以发挥不同测量方法的特长。Shen[2]等通过主动视觉系统和接触式CMM的集成,实现了由视觉测量进行曲面识别和粗定位,然后指引CMM进行高精度测量的功能。为使激光测头和接触式测头实现优势互补,已有公司开发出实现激光扫描头和接触扫描头互换的坐标测量系统[3]。
尽管非接触式激光三角形法在逆向工程中应用发展较快,但鉴于接触式CMM测量与非接触式激光测量各有特点,它们在逆向工程中的应用各有侧重,相互补充。对于曲面形状复杂,且精度要求也很高的零件,有时用接触式坐标测量机测量是最佳乃至唯一的选择[4]。
根据三坐标测量机测头半径补偿时间可以将补偿分为在线自动补偿和离线数据处理补偿。目前的CMM测量中,广泛采用一种二维在线自动补偿方法,即在测量时,将测量点和测头半径的关系都处理成二维情况,在测量时自动完成数据的测头半径补偿。对一些由规则形状组成的表面的测量,如平面、二次曲面,二维补偿是精确的。但对于一些由自由曲面组成的复合曲面,测量方向和测量点的法矢有可能不一致,用二维补偿方法进行补偿会造成补偿误差。在误差不能忽略的情况下,必须考虑对测量进行测头半径的三维补偿。
文献[5-11]研究了测头半径的三维补偿,其中有的方法不适用于接触式密集数据采集测头半径补偿;有的方法[7,8]可用于接触式密集数据采集测头半径补偿,但在补偿过程中存在较多中间处理环节,导致补偿处理时间较长和补偿精度不理想。本文拟开展基于自组织特征映射(SOFM)神经网络[12]的接触式密集数据采集测头半径三维智能化补偿研究,以在测头半径补偿效率和补偿精度层面有所推进。
1 测头半径的三维补偿模型
1.1 三角形网格自组织压缩重建
用于散乱点数据压缩的SOFM神经网络二维阵列模型如图1所示。图中网络的输入矢量就是复杂曲面上的测点矢量Pj(x,y,z),网络输出层具有m×n个神经元结点。网络神经元对曲面空间测量样本点的学习和训练来模拟曲面上的点与点之间的内在关系,结点连接权矢量集{Wi}重构曲面样本点的内在拓扑关系及实现对测点集{Pj}的工程近似化,实现曲面三维散乱点云的自组织压缩,构成三角剖分。
图1所示神经网络的权重调节算法如式(1)所示。
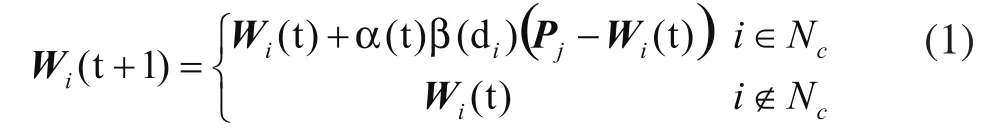
式中Pj为测点矢量;Wi(t)为连接权矢量;α(t)为修正率;Nc为以结点c为中心的输出结点集合,如图2所示,其中c为与输入矢量Pj匹配最佳的输出结点;β(di)是修正率加权函数,其中di为邻区集合Nc中结点i到c之间的距离。按六角形阵列侧抑制邻区Nc训练调整网络神经元权重矢量,使网络输出层结点呈六角形阵列分布,可生成测量点集压缩后的Delaunay三角逼近剖分。
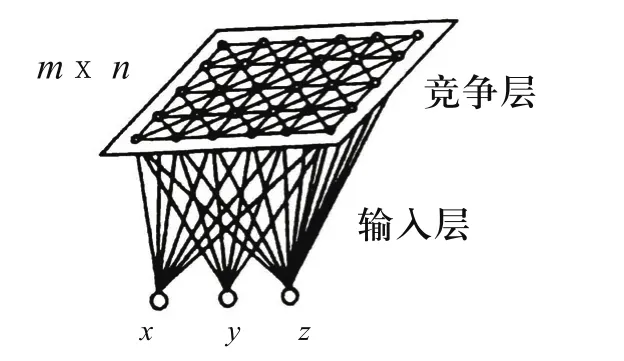
图1 数据压缩二维阵列网络模型
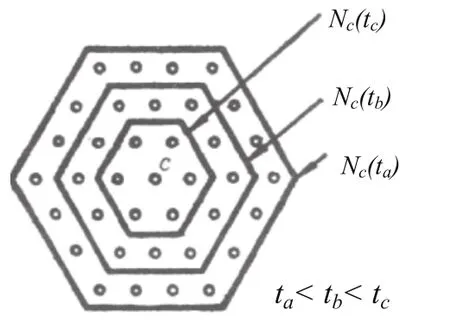
图2 六角形阵列邻区Nc
1.2 三角形网格顶点法矢
设欲重构的曲面可以用参数方程表示如式(2):

式中P表示曲面的笛卡儿坐标(x,y,z),Q表示曲面参数(u,v) 。对于曲面采样测点矢量集,曲面参数可设为(x,y)。
基于自组织特征映射神经网络的曲面重建模型有赖于SOFM神经网络的扩展,即利用无导师SOFM神经网络学习能力,由神经网络系统自己建立曲面参数方程表达式(2)。此式是一复杂的非线性变换,要用一个函数拟合所测得的数字化点群数据是困难的。为此可将式(2)在Qs处台劳展开:
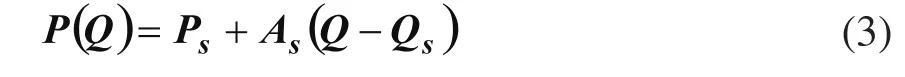
式中Ps,As和Qs可用扩展SOFM(ESOFM)神经网络学习而得。此式表示所构造的神经网络权重矢量Ps处的微切平面方程。依据此式,微切平面(3)逼近曲面(2),在Qs局域Fs中可达到很高的精度。Fs由下式定义:
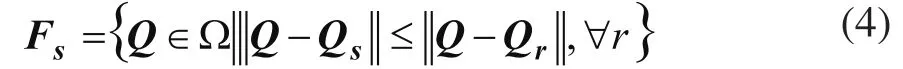
式中s是激活神经元,Fs是神经元s对应的输入空间,即感受野;Ω是输入空间;Qr是神经元r的外部输入权重,即分类核心。
r为自组织特征映射神经网络阵列中的神经元,初始时,其外部输入权重Qr随机均布在输入空间Ω。SOFM自组织学习算法可使r与Qr形成空间有序特征映射。通过SOFM算法扩展同时使r与(Pr, Ar)建立映射关系。Pr及Ar以随机函数定义初始值。通过ESOFM神经网络训练,学习Pr, Ar及Qr,以满足式(3)。
按前述建立的ESOFM神经网络中,每一个神经元s有一个感受野Fs以及外部输入权重Qs,那么该神经元的输出就是Ps。当输入Q偏离Qs时,则神经元的输出由式(3)得到。这样ESOFM神经网络将整个数字化点群数据分成许多子区域,每个子区域用一个线性函数逼近(即微切平面逼近),每组权重各自对相应的子区域负责。当区域分得足够细时,即神经元数目足够多时,拟合精度可以达到所要求的程度。式(3)中的As可用于计算相应子区域权重矢量Ps(即三角形网格顶点)处的法向矢量ns,其计算公式如下:
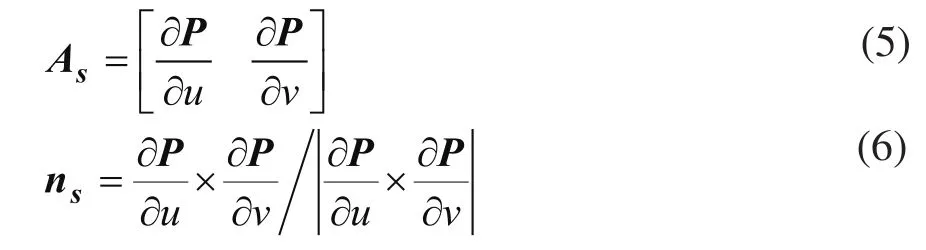
式中As由ESOFM神经网络训练后直接得到。
1.3 测头半径三维补偿
测头半径补偿的关键是确定曲面在接触点处的法矢。测头与被测曲面接触时,球心一定在被测点的法线上,而且被测点一定在球心轨迹面过球心点的法线上。因此不论是得知被测面的法线方向或是球心面的法线方向,都能对测头半径进行补偿。对于未知CAD模型的样件的测头半径补偿,只有根据测量点集信息计算通过球心点的法矢。
上述ESOFM神经网络经过训练,可得到三角形网格顶点{Pr}(逼近测头球心点集)及其法矢{nr},由此可以按式(7)计算测头与工件的接触点集{Pb}。

式中r为测头半径。
2 测头半径补偿的仿真实验
2.1 采用球面模型的仿真实验
仿真实验中,测头半径补偿模型中的神经元阵列包含m×n个神经元(具体分别取三种组合:8×10,10×12,12×13),采用球面模型进行仿真实验,测头半径为1mm,仿真实验结果如图3所示。
球面的参数方程如下。
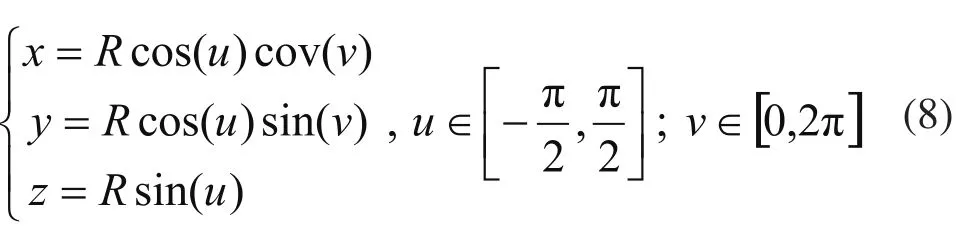
图3(a)表示的采样点集作为测头球心仿真测量的坐标点集(密集散乱点集),测头球心球面采样的参数范围为:u=0~π/7,v=0~π/6,R=10mm。采样点集包含1320个点,其中边界点集包含120个点;图3(b)表示逼近测头球心点集的三角形网格及网格顶点处的法矢,图中也绘制了边界点集(m×n=8×10);图3(c)表示工件球面为凸球面时,采样点集经过压缩及测头半径补偿后生成的三角形网格(逼近测头与工件的接触点集,m×n=8×10);图3(d)表示工件球面为凹球面时,采样点集经过压缩及测头半径补偿后生成的三角形网格(逼近测头与工件的接触点集,m×n=8×10);图3(e)表示测头半径补偿模型中的神经元阵列包含10×12个神经元的测头半径补偿仿真实验结果(工件球面为凹球面);图3(f)表示测头半径补偿模型中的神经元阵列包含12×13个神经元的测头半径补偿仿真实验结果(工件球面为凹球面)。
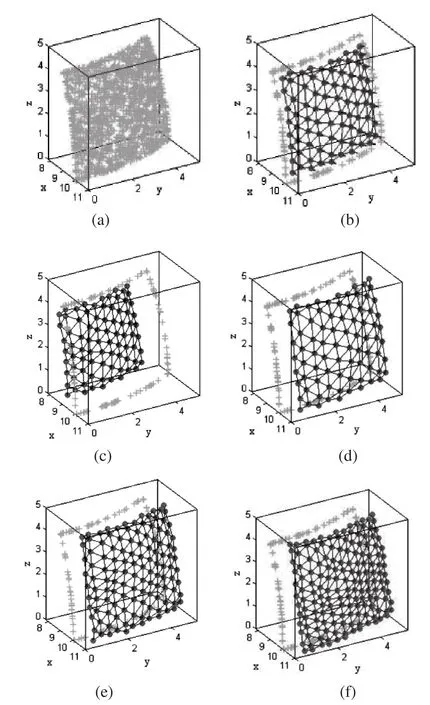
图3 仿真实例1
仿真实验中经过采样数据压缩和测头半径三维补偿后生成的三角形网格逼近理想工件球面的逼近精度如表1所示。表1中分别表示了图3(d)~(f)仿真实验的逼近精度。
表1中Ds表示三角形网格逼近测头球心面的精度;Dw表示三角形网格逼近工件表面的精度;Dwmax表示Dw中的最大值;Dwmin表示Dw中的最小值;T表示神经网络训练时间。三角形网格的逼近精度表示三角形网格顶点集逼近曲面的程度,本文按(9)式进行计算度量。
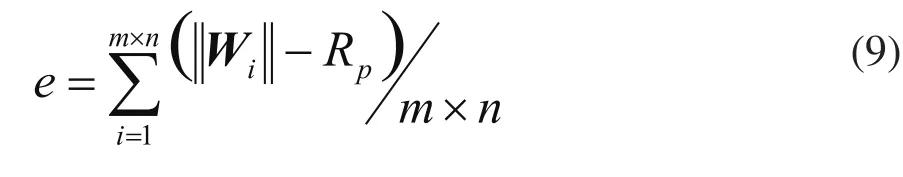
式中m×n表示测头半径补偿模型中的神经元阵列所包含的神经元;Rp为理想工件球面的半径。图3(c)所示情况下,Rp取为9mm;图3(d)~(f)所示情况下,Rp取为11mm。Wi表示三角形网格顶点的权重矢量,即三角形网格顶点的空间位置。
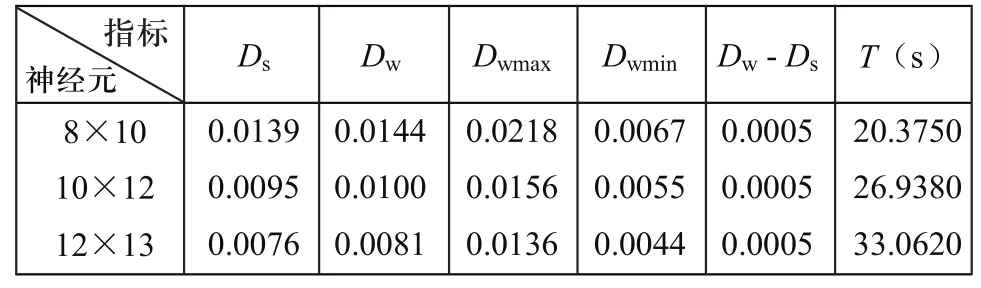
表1 仿真实验的精度(距离单位:mm)
2.2 采用复杂曲面模型的仿真实验
仿真实验中,测头半径补偿模型中的神经元阵列包含12×15个神经元,采用复杂曲面模型进行仿真实验,测头半径为1.5mm,仿真实验结果如图4所示。
图4(a)表示测头球心仿真测量采样点集,测头球心扫掠的曲面如公式(10)所示,按照Δx=Δy=π/60cm进行采样,得到有序采样点集。采样的参数范围为:x=3π/4~5π/4,y=π/3~5π/6。测量点集包含961个点;图4(b)表示逼近测头球心仿真测量采样点集的三角形网格及网格顶点处的法矢;图4(c)表示工件表面为凸面时,采样点集经过压缩及测头半径补偿后生成的三角形网格(逼近测头与工件的接触点集)。
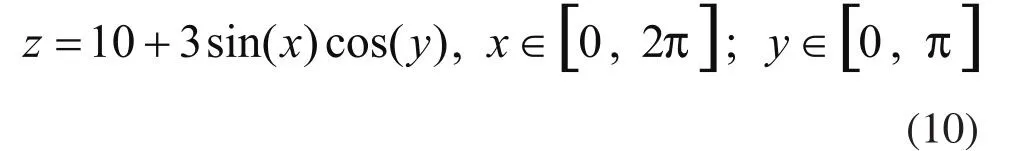
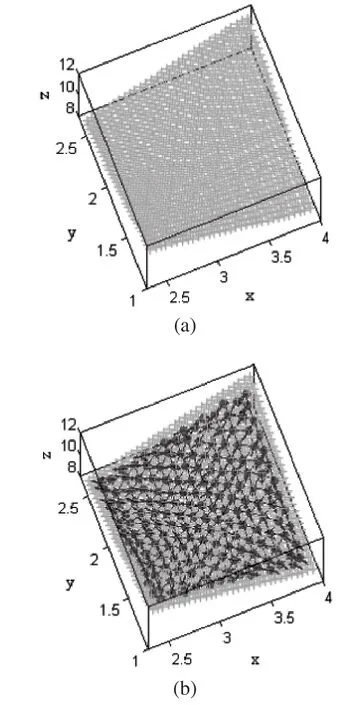
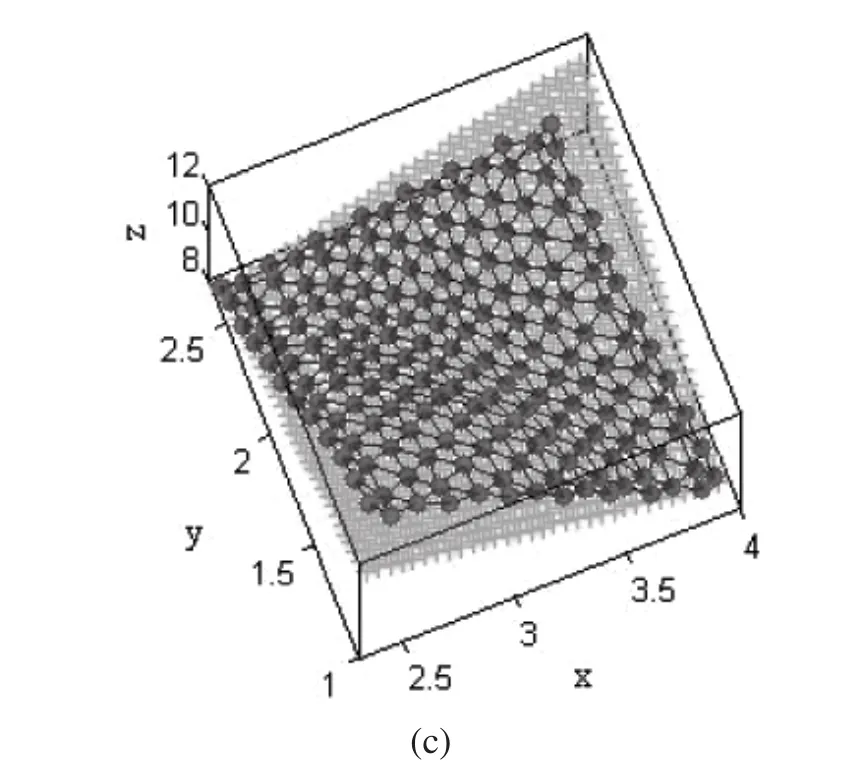
图4 仿真实例2
无论是简单曲面球面的密集散乱仿真测量点集还是复杂曲面的密集有序仿真测量点集作为仿真实验对象,在仿真实验层面均验证了所构建的测头半径三维补偿模型的有效性。在采用球面模型的仿真实验中可以得到:1)Dw- Ds的值为亚微米级,非常微小,这可以间接证明所求的测头半径补偿法矢非常接近理想补偿法矢;2)随着神经元数目增加,补偿后的三角形网格逼近理想工件表面的精度Dw得到提高,Dw精度可以满足工程需要;3)补偿后的三角形网格存在边缘误差,即三角形网格的边界网格顶点偏离测头与工件表面的接触点集中的边界点集,通过增加神经元数目可以减小边缘误差。测头半径补偿模型在采用复杂曲面模型的仿真实验中,呈现出其在采用球面模型的仿真实验中相同的效果。
3 结束语
基于三坐标测量机的接触式连续扫描测量采集的坐标数据是测头中心的坐标值,而非测头与被测量件的接触点的坐标值。为了拟合出较精确的曲面,必须对测头半径进行三维精确补偿。本文构建的三坐标测量机接触式数据采集测头半径三维智能化补偿模型,实现了未知CAD模型零件的接触式密集数据采集测头半径三维补偿。如此得到的经过密集测量数据压缩与测头半径补偿的逼近零件表面的三角形网格,既可用于构造散乱数据插值曲面的前置处理,也可用于快速原型STL格式的零件几何表示。本文的研究工作对我国有关先进制造业如汽车业、摩托车业、模具业、五金业、家电业等行业的产品创新逆向工程具有重要意义。
[1]柯映林,等.反求工程CAD建模理论、方法和系统[M].北京:机械工业出版社,2005:1-13.
[2]Shen T Z,Huang J B,Menq C H.Multiple-sensor integration for rapid and high-precision coordinate metrology[J].IEEE/ASME Trans.on Mechtronics,2000,5(2):110-121.
[3]中国模协技术委员会模具评定评述专家组.第八届国际模展模具先进制造技术评述[J].电加工与模具,2000,4:1-6
[4]石照耀,谢华锟,费业泰.复杂曲面测量模式与关键技术[J].工具技术,2000,34(11):31-34.
[5]Suh S H,Lee S K,Lee J J.Compensating probe radius in free surface modeling with CMM:Simulation and experiment[J].Int.J.Prod.Res.1996,34(2):507-523.
[6]李春,刘书桂.三坐标测量机的测头半径补偿与曲面匹配[J].仪器仪表学报,2003,24(4):145-147.
[7]Shuh Ren Liang,Alan C.Probe-radius compensation for 3D data points in reverse engineering[J].Computer in Industry,2002,48:241-251.
[8]Mayer J R,Mir Y A,Vafaeesefat A,et al.Touch probe radius compensation for coordinate measurement using kriging interpolation[J].Proc.Instn.Mech.Engrs.1997,211(Part B):11-18.
[9]Menq C,Chen F L.Curve and surface approximation from CMM measurement data[J].Computers ind.Engng.,1996,30(2):211-225.
[10]Xiong Z H,Li Z X.Probe radius compensation of work-piece localization[J].Transactions of ASME,Journal of Manufacturing Science and Engineering,2003,125(1):100-104.
[11]刘荷辉,虞钢.自由曲面的二维自适应测量及测球半径的三维补偿[J].机械工程学报,2004,40(2):117-120.
[12]Kohonen T.Self-organizing maps[M].Springer,1997.

