一道经典习题的其他结论

442706 湖北省丹江口市习家店中学 王有华

一道经典习题的其他结论

442706 湖北省丹江口市习家店中学 王有华

等边三角形是最特殊、最具有美感的三角形，具有很多特殊的性质，值得探究的地方很多，为各类练习、考试命题提供了丰富的素材.本文从一道经典的习题入手，探究两个有公共顶点的等边三角形的一些结论.

如图1，C是线段AB上一点，以分别AC，BC为边在线段AB的同侧作等边△ACD，等边△BCE，连接AE，BD.

(1)求证：AE=BD;

(2)如图2，将等边△BCE绕点C顺时针旋转一定角度，以上结论是否还成立，如果成立，给出证明，如果不成立，请说明理由.

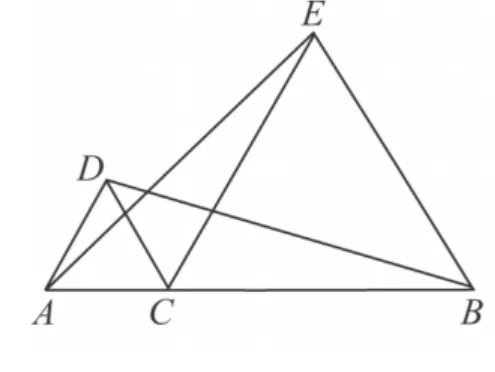
图1

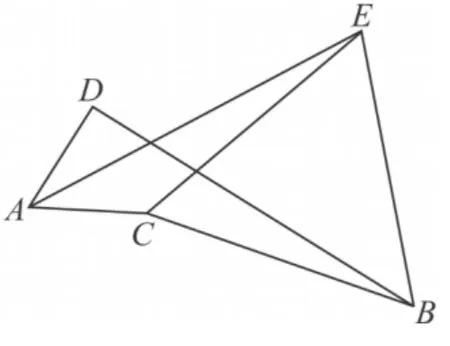
图2

本题是一道经典的运用等边三角形的性质、图形变换、全等三角形的判定的动态习题，很多版本的教材都不约而同的将它选为例题或练习.这两个小题都是证明△ACE≌△DCB，从而得出AE=BD.

其实，对这个问题，在条件不变的前提下，还有其他一些结论，下面对此进行探究.

结论1 如图3，将等边△BCE绕点C旋转，当点A，D，B三点在同一直线上时，AE+AC=AB.

证明 连接 AE，BD，易证ACE≌△DCB，

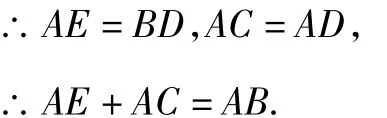
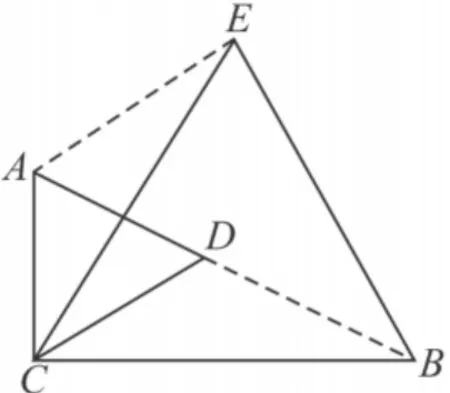
图3

结论2 如图4，C是线段AB上一动点，以分别AC，BC为边在线段AB的同侧作等边△ACD，等边△BCE，连接 AE，BD，AE 与 DC 交于点M，BD与CE交于点N，连接 MN，无论点 C运动到什么位置，都有 BN=EM，△MCN为等边三角形.

证明 易证△ACE≌△DCB，

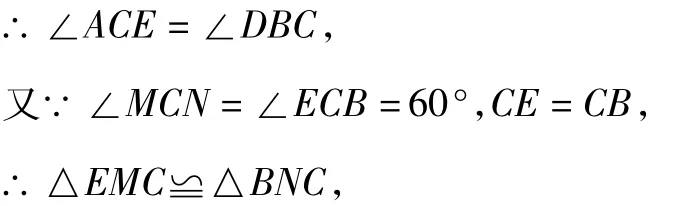
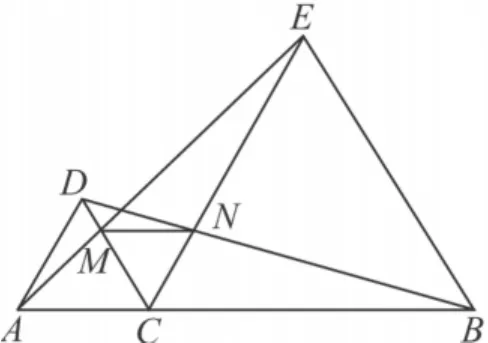
图4

结论3 如图5，C是线段AB上一动点，以分别 AC，BC为边在线段AB的同侧作等边△ACD，等边△BCE，过点D作 DF⊥AB于 F，过点 E作EG⊥AB于 G，无论点 C运动到什么位置，直角梯形DFGE的面积恒为定值.

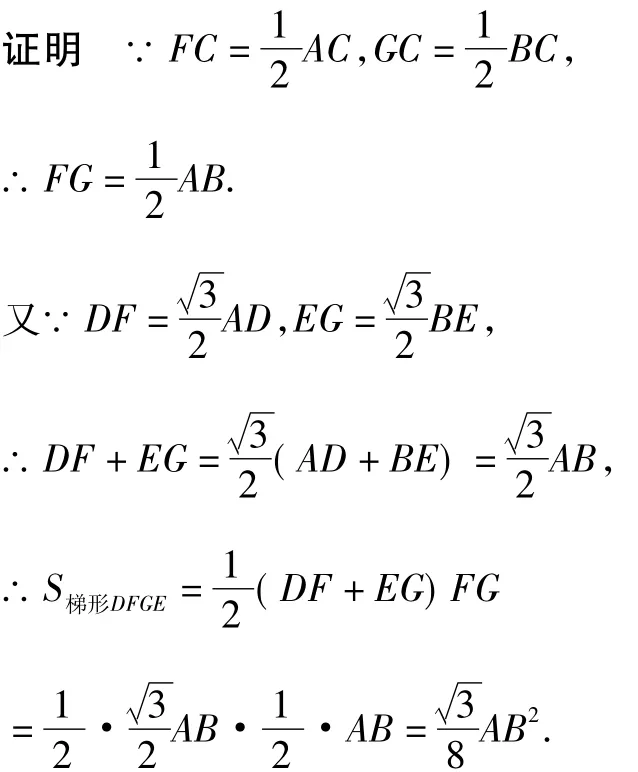
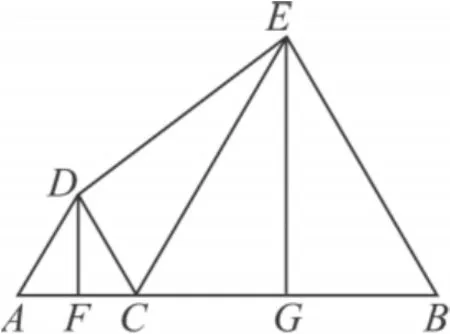
图5

结论4 如图6，C是线段AB上一动点，分别以AC，BC为边在线段AB的同侧作等边△ACD，等边△BCE，连接D，E，P为线段DE的中点，无论点C运动到什么位置，点P到线段AB的距离恒为定值.

证明 作PH⊥AB于H，取AC的中点F，BC的中点G，连接 PF，PG.

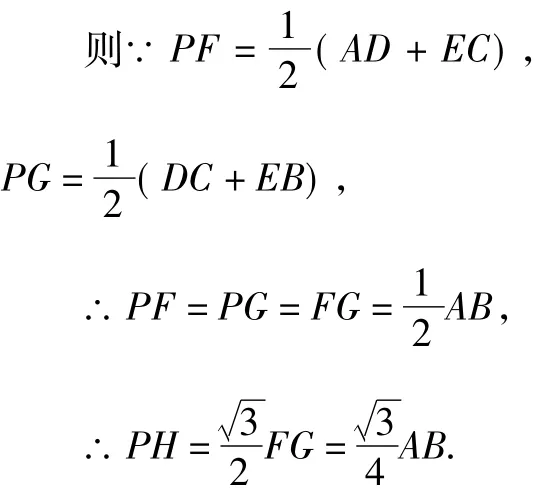
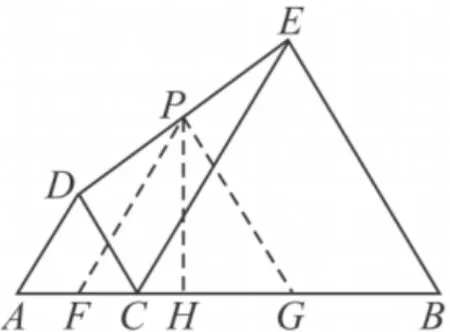
图6

结论5 如图7，将等边△BCE绕点C旋转任意角度，G为线段AE的中点，H为线段BD的中点，则△CGH为等边三角形.

证明 因为△ACE≌△DCB，

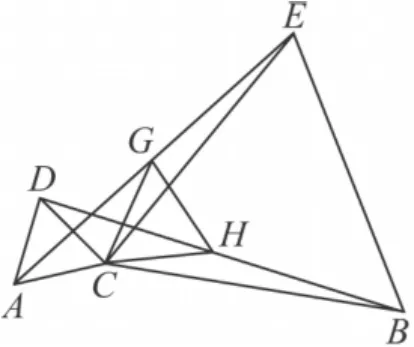
图7

∴△CGH为等边三角形.

结论6 如图8，将等边△BCE绕点C旋转任意角度，直线AE、直线BD所夹的锐角都等于60°.

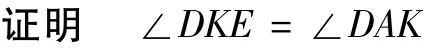
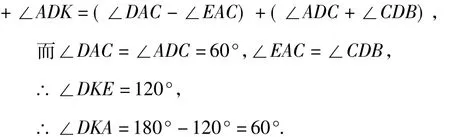
结论7 将等边△BCE绕点C旋转，当点E在直线AD上时，BD∥AC.

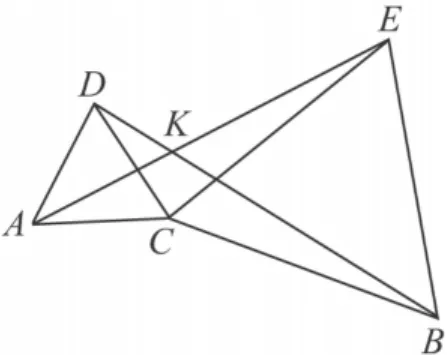
图8

证明 如图9，当点E在线段AD上时，

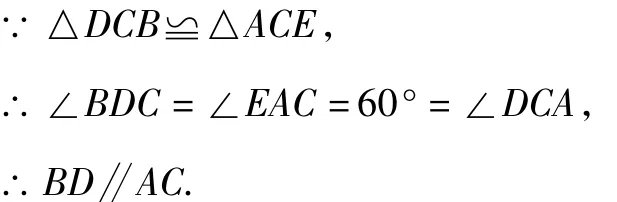
如图10，图11，当点E在线段AD的延长线或反向延长线上时，同理可证BD∥AC.

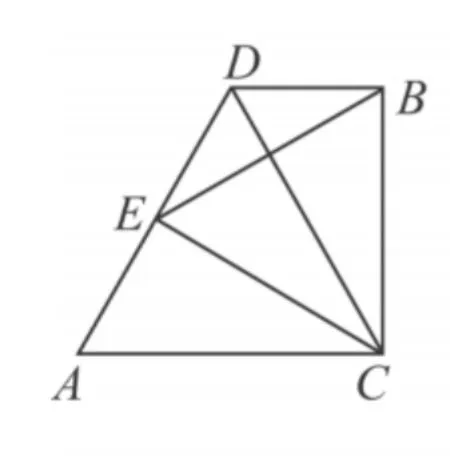
图9

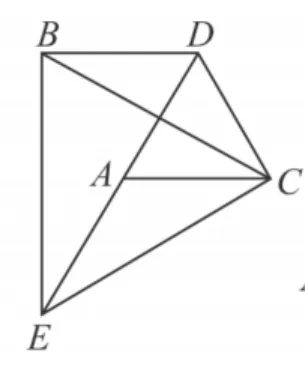
图10

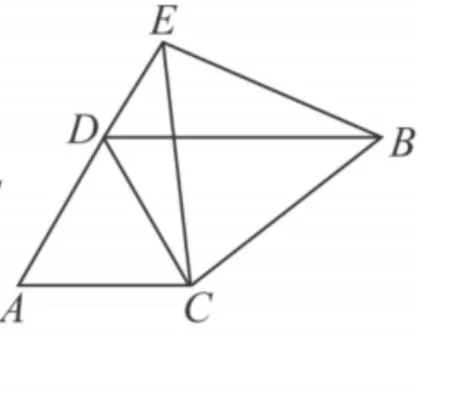
图11

结论8 如图12，将等边△BCE绕点C旋转任意角度，直线 AE，直线 BD的交点为K，则等边△ACD的外接圆与等边△BCE的外接圆都经过交点K.

证明 ∵∠DKA=∠DCA，

∴ 点A，D，C，K 四点共圆，同理点B，E，C，K 四点共圆，

∴等边△ACD的外接圆与等边△BCE的外接圆都经过交点K.

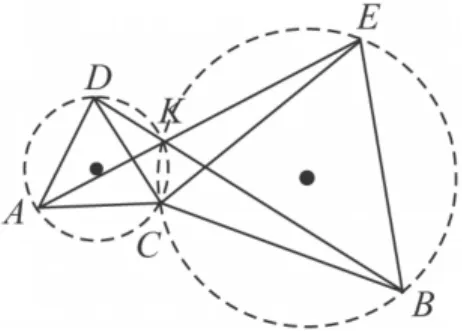
图12

结论9 如图13，将等边△BCE绕点C旋转任意角度，过点A作CB的平行线AF，过点B作AC的平行线BF，AF，BF相交于点 F，则△DEF为等边三角形.

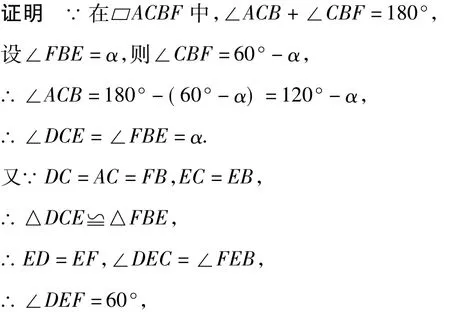
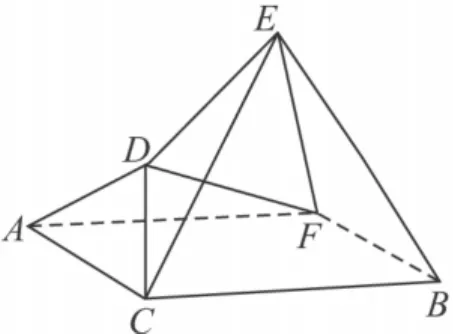
图13

∴DEF为等边三角形.

结论10 如图14，将等边△BCE绕点C旋转，当点A在△BCE内部，且∠CAE=150°时AC2+AE2=AB2.

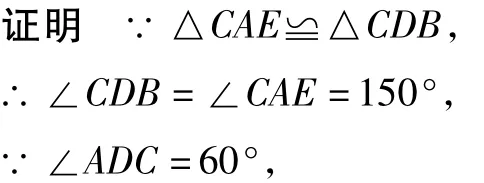
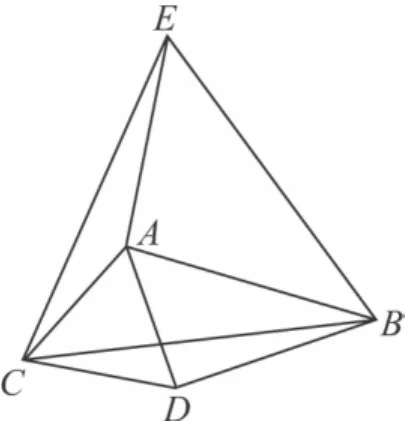
图14

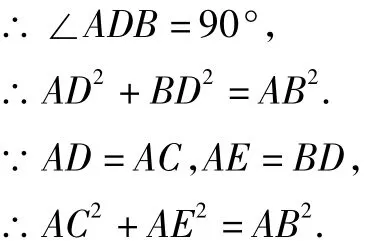
以上是对两个有公共顶点的等边三角形进行变换探究得出的一些结论，这些结论对于引导师生钻研经典几何问题，达到“一题多变，触类旁通，连成体系”有较好的效果.

20111005)