基于SIFT特征的无人机航拍图像拼接

乔文治

（洪都航空工业集团,江西南昌330024）

基于SIFT特征的无人机航拍图像拼接

乔文治

（洪都航空工业集团,江西南昌330024）

无人机在飞行过程中由于机体的倾斜和抖动，造成航拍图像出现大的仿射变形。因此，传统的图像拼接算法很难得到好的效果。基于SIFT(Scale Invariant Feature Transform)特征的图像拼接算法，首先通过提取图像的尺度不变特征点，解决了待拼接图像间大的平移、旋转、尺度变化的干扰。然后，通过欧式距离判断得到初匹配特征点集，并利用RANSAC方法进一步精确了匹配点集，得到了准确的变换矩阵；最后，采用加权平均法的图像融合技术，得到了稳定的、鲁棒的图像拼接结果。

图像拼接；航拍图像；SIFT；特征匹配

0 引言

无人机(Unmanned Aerial Vehicle，UAV)具有机动性强，反应灵活，价格低等特点，无论在军事还是民用上都有广泛的运用前景。获取高分辨率、能描述场景的二维或三维图像是它的主要任务之一，但无人机遥感平台在获取图像时，因受到其飞行高度和CCD相机焦距的限制，单张航拍图像很难包含所有的目标区域，因此，图像拼接已成为无人机航拍图像处理的关键问题之一。

图像拼接（Image Mosaics）通常都是将数张有重叠部分（包括不同时间、不同视角、不同传感器）的图像拼成一副大型的无缝高分辨率图像的技术。图像拼接的方法可分为两大类：基于空间域和基于频域。基于频域的算法主要利用傅里叶变换将图像转换到频域进行拼接计算。例如，Fourier-Mellin算法，相位相关法等。这类算法速度快，但准确性较差；基于空间域的图像拼接算法是目前研究的热点。1996年，R.Szeliski[1]将八参数投影变换模型用于图像配准，然后利用LM算法（Levenberg-Marquardt迭代非线性最小化方法）搜索参数空间获得变换参数。这种算法对平移、旋转变换有效，但当图像发生大的尺度等仿射变换时，用这种方法并不能得到很好的效果。1997年，他在文献[2]中改进了这种算法，提出了通过迭代求精每幅图像对应的旋转矩阵和摄像机焦距来实现拼接的方法，这种经典的理论体系仍被沿用至今。当前基于空间域的算法中，基于图像特征的拼接算法已成为研究的主流。2003年，M.Brown和D.G.Lowe[3]提出了一种基于SIFT不变量的图像拼接算法，这种算法适应性强，准确率高，而且算法完全自动完成且效果很好。2004年，赵向阳，杜立民[4]利用Harris算法提取角点并进行匹配，然后采用鲁棒变换估计待拼接图像的变换矩阵。这种算法在一定程度上提高了配准算法的稳健性，但是计算速度比较慢。2008年，李玲玲[5]提出了一种SIFT和Harris-Affine互补不变特征匹配的自动拼接算法，该算法去除了图像序列的尺度、旋转等几何变形与光照的影响，实现了大矢量图像的自动拼接。但由于Harris-Affine的迭代算法速度很慢，从而导致拼接算法速度变慢。

虽然近年来图像拼接技术不断涌现，但是，用这些方法对无人机获取的航拍图像进行拼接仍存在很多困难。首先，无人机获取的图像具体数据量大、重叠度高，为了快速的得到大视场图像就必须使用图像快速自动拼接系统来处理它的航拍图像图像；其次，无人机体积比较小,自稳定性和抗风能力差,虽然装有自动驾驶与增稳陀螺,但是在拍照的过程中不可避免地会出现倾斜、抖动,相机本身也存在镜头的几何畸变,因此无人机拍摄的图像相对于真实场景都有大的仿射变形。

本文针对无人机航拍图像的特点，选择能适应大的平移、旋转及尺度不变性的sift特征作为图像的拼接特征，对不同拍摄条件下获取的无人机航拍图像进行了拼接。试验结果表明，这种方法速度快，准确性好，为无人机的航拍图像处理提供了一种可行的方法。

1 无人机航拍图像拼接流程

根据无人机航拍图像的特点，图像拼接由四部分组成：图像几何校正、图像配准、变换矩阵计算、图像融合。几何校正是对成像过程中所产生的一系列畸变进行校正，产生一幅符合某种地图投影或图形表达要求的新图像，并且将变形的图像纠正，统一到建立的坐标系中，建立测量地物的坐标信息[6]。图像配准是指对图像间的匹配信息进行提取，在提取出的信息中寻找最佳的匹配，完成图像间的对齐。图像配准是图像拼接最关键的步骤。图像融合是指在配准以后对图像进行缝合并平滑边界，让图像过渡自然。图像拼接的流程如图1所示。其中，图像配准与融合是流程中最主要的步骤。

图1 图像拼接流程

2 无人机航拍图像的配准

无人机航拍图像的配准主要有两个步骤：特征提取和特征匹配。图像配准算法一般可以分为基于频率域和基于空间域两类方法。由于无人机图像有高重合度和大数据量的特点，所以选择基于特征的配准方法更为合适。

2.1 SIFT特征提取

本文利用SIFT特征检测器在图像的尺度空间内进行特征检测，确定特征点在图像上的精确位置以及该特征点的尺度。首先，利用二维高斯核函数对图像进行尺度变换，得到图像多尺度空间的系列信息。二维高斯核函数

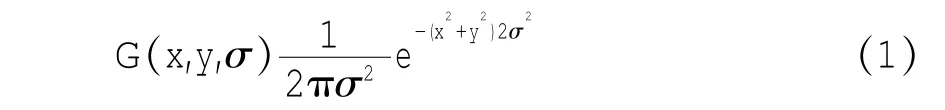
图像的尺度空间L（x,y,σ）可表示为：

式（1）、（2）中，σ 为尺度参数，I(x,y)表示输入图像，*为在图像坐标(x,y)处的卷积运算。然后，对尺度空间L（x,y,σ）的第二层进行下采样，并继续进行上述高斯卷积，重复多次这样的计算后得到高斯金字塔。最后，为得到具有良好的独特性（Distinctiveness）和稳定性 （Stability）的特征的，在图像二维平面空间和DoG(Difference-of-Gaussian)尺度空间中同时检测局部极值以作为特征点。DoG算子定义为两个不同尺度的高斯核的差分，是归一化LoG (Laplacian-of-Gaussian)算子的近似。DoG算子如式(3)所示：

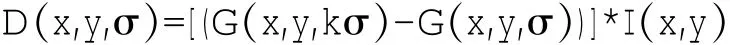
对于图像上的点，计算其在每一尺度下DoG算子的响应值，这些值组成了特征尺度轨迹曲线。特征尺度曲线的局部极值点即为该特征的尺度。尺度轨迹曲线上完全可能存在多个局部极值点，这时可认为该点有多个特征尺度。

2.2 SIFT特征匹配

SIFT特征匹配算法包括两个阶段，第一阶段是SIFT特征向量的生成，即从多幅待匹配图像中提取出对旋转、尺度、亮度变化无关的特征向量；第二阶段是SIFT特征向量的匹配。

2.2.1 SIFT特征向量的生成(图2）

根据《山西省抗旱应急水源工程实施方案编制有关技术要求（试行）》的要求，本次抗旱应急水源工程基准年为2013年，规划水平年为2025年。2013年项目区人口为10 350人，人口自然增长率为6‰，设计用水居民人数按下式计算：

1）通过拟和三维二次函数以精确确定关键点的位置和尺度，同时去除低对比度的关键点和不稳定的边缘响应点 (因为DoG算子会产生较强的边缘响应)，以增强匹配稳定性、提高抗噪声能力。

2）利用特征点邻域像素的梯度方向分布特性为每个关键点指定方向参数，使算子具备旋转不变性。

m（x,y）和 θ（x,y）分别为特征点领域像素（x,y）处梯度的模值和方向公式。其中L所用的尺度为每个关键点各自所在的尺度。在实际计算时，在以关键点为中心的邻域窗口内采样，并将邻域像素的梯度方向用直方图统计。梯度直方图的范围是0～360度，其中每10度为一个柱，总共36个柱。直方图的峰值则代表了该关键点处邻域梯度的主方向，即作为该关键点的方向。

在梯度方向直方图中，当存在另一个相当于主峰值80%能量的峰值时，则将这个方向认为是该特征点的副方向。此时，一个特征点可能会存在多个方向（一个主方向，一个以上副方向），这样做可以增强匹配的鲁棒性。至此，每个关键点有三个信息：位置、尺度和方向。由此可以确定一个SIFT特征区域。

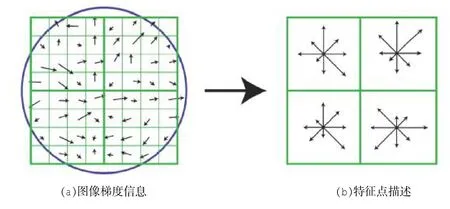
图2 特征点邻域梯度信息生成SIFT特征向量

3）生成SIFT特征向量。为确保特征的旋转不变性，首先将图像坐标轴旋转为特征点的主方向，然后以特征点为中心取8×8的窗口。假定图2（a）的中心点为当前特征点的位置，每个小格代表特征点邻域所在尺度空间的一个像素，箭头长度代表梯度模值，箭头方向代表该像素的梯度方向，图中蓝色的圈代表高斯加权的范围 （越靠近特征点的像素梯度方向信息贡献越大）。然后在每4×4的小块上计算8个方向的梯度方向直方图，绘制每个梯度方向的累加值，即可形成一个种子点，如图2（b）所示。此图中一个关键点由2×2共4个种子点组成，每个种子点有8个方向向量信息，特征向量共32维。这种邻域方向性信息联合的思想增强了算法抗噪声的能力，同时对于含有定位误差的特征匹配也提供了较好的容错性。实际计算过程中，为了增强匹配的稳健性，Lowe建议对每个关键点使用4×4共16个种子点来描述，这样对于一个关键点就可以产生128个数据，即最终形成128维的SIFT特征向量。此时SIFT特征向量已经去除了尺度变化、旋转等几何变形因素的影响，再继续将特征向量的长度归一化，则可以进一步去除光照变化的影响。

2.2.2 生成SIFT特征初匹配集

当两幅图像的SIFT特征向量生成后，采用特征向量的欧式距离来作为两幅图像中特征点的相似性判定度量。取图像1中的某个特征点，并找出其与图像2中欧式距离最近的前两个特征点，在这两个特征点中，如果最近的距离除以次近的距离少于某个比例阈值，则接受这一对匹配点。降低这个比例阈值，SIFT匹配点数目会减少，但更加稳定。

3 变换矩阵计算

使用RANSAC算法能够对SIFT特征点初匹配结果进行精确筛选，并且找出一个图像之间的投影变换单应矩阵，进而达到拼接的目的。它的基本思想是进行参数估计时，不是不加区分地对待所有可用的输入数据,而是首先针对具体问题设计出一个目标函数，然后迭代地估计该函数的参考值，利用这些初始参数值把所有的数据分为所谓的“内点”(即满足估计参数的点)和“外点”(即不满足估计参数的点)。最后反过来用所有的“内点”重新计算和估计函数的参数。RANSAC方法和传统方法的区别在于传统的方法把全部的数据点作为内点和外点，而RANSAC最开始是利用一部分数据作为内点得到初始值,然后寻找数据集中所有别的内点。使用RANSAC估计方法,可以最大限度地减少噪声及外点的影响。

4 图像融合

在完整的拼接图中要求拼合的过渡区域不能出现明显的痕迹。无人机航拍图像由于拍摄角度、时间不同，图像序列间会存在一定的视角变化和光照差异。另外，由于拍摄的高度不同，图像目标有时也会发生尺度变化，这些因素都会影响拼接的质量，比如在重叠区域内出现鬼影、模糊，或者在重叠边界处出现明显的拼缝。因此，当图像变换到同一坐标系下后，还需要进行融合处理，使拼接符合视觉效果。

图像的融合规则是图像融合的核心,图像融合规则的好坏直接影响融合图像的速度和质量。这其中有：基于像素选取的融合规则、考虑分解层内图像及分解层间相关性的像素选取融合规则等。

图像融合的算法有很多,简单的有光强平均融合、加权平均融合、中值滤波法、采样权重函数法，复杂的有图像Voronoi权重法、高斯样条插值法、基于欧氏距离的有效权重法等。但不同的图像之间都存在着程度不同的差异，如果简单的对图像的共同区域数据进行叠加，会出现图像模糊、灰度变化不连续等现象。同时，由于图像的复杂性和多样性，使得无法精确地计算出两幅图像间的变换参数，所以我们很难提出一种精确的融合算法从根本上消除拼接痕迹。

综合比较以上各种融合算法，光强平均融合法的速度最快，但效果欠佳;多分辨率样条方法的融合质量最高，但运算量过大;而加权平均法在速度和效果两者中取得较好的平衡，在运算量不大的情况下保证了较好的融合质量。因此，本文选择使用加权平均法完成图像融合。

5 试验结果

为使算法得到客观评价，本文对大量真实场景的航拍图像进行拼接，选择用来做试验的图像序列包括大场景图像，大仿射变化与光照变化的图像等。试验中，最近邻域特征点距离与次领域特征点距离之比为0.6。

试验一：

图3是对一组存在光照、尺度与旋转变化的航拍图像的匹配与拼接结果。可以看出，在干扰因素较多的环境下，基于SIFT特征的图像拼接算法通过尺度不变特征的检测与特征向量的归一化处理，消除了光照影响与图像尺度变化的影响，因此能得到很准确的图像匹配特征（图3（c）），这对求解两图像间的变换矩阵是至关重要的。算法求解的变换矩阵为(0.980945，-0.204663，179.870102；0.207166，0.980328，77.799866；0.000004，0.000005，1）。 由于无人机飞行的抖动和传感器镜头扭曲等原因，图像的拼接结果（图3（d））出现了边缘畸变，但拼接结果同时也显示了这种方法的稳定性与鲁棒性。

试验二：

图4是对三幅图像的拼接结果。其中，图4（d）相对图4（a）和图4（c）存在着大的光照变化，三幅图都相互存在着旋转、尺度的变化，由于本文的算法采用的SIFT特征对大尺度的变换与光照变化保持不变性，因此同样能得到很好的拼接结果。

图3 图像匹配和拼接结果1

图4 图像匹配和拼接结果2

6 结论

本文针对无人机航拍图像的特点，将SIFT特征作为图像拼接特征。在利用欧式距离对特征初匹配的基础上，采用RANSAC算法，得到了更为精确的匹配集，并计算了图像序列的变换矩阵。由于SIFT特征对图像的旋转、尺度和光照保持不变性，本文的算法得到了稳定的、鲁棒的拼接结果。

[1]R.Szeliski.Video mosaics for virtual environments.IEEE Computer Graphics and Applications,1996,16(2),3:22-30

[2]R Szeliski,H Y Shum.Creating Full View Panoramic Image Mosaics and Environment Maps.In Proc.of ACM SIGGRAPH,1997,251-258.

[3]D.G.Lowe.Distinctive image features from scaleinvariant keypoints [J].International Journal of Computer Vision,2004,60(2):91-110.

[4]赵向阳,利民.一种全自动稳健的图像拼接融合算法.中国图形图像学报,2004,9(4):417-422.

[5]李玲玲，李翠华，曾晓明，李保.基于Harris-Affine和SIFT特征匹配的图像自动配准.华中科技大学学报（自然科学版），2008，36（8）：13-16.

[6]谢利理,李玉忍,齐蓉.航空照片数字地图的几何校正.西北工业大学学报,2001,19(4):617-620.

>>>作者简介

乔文治，男，1980年4月出生，2002年毕业于武汉工程大学，2011年获北京航空航天大学工程硕士学位，工程师，现从事科技项目管理工作。

Aerial Images Mosaic for Unmanned Aerial Vehicle Based on SIFT Features

Qiao Wenzhi
(Hongdu Aviation Industry Group,Jiangxi Nanchang 330024)

During the flight of unmanned Aerial Vehicle(UAV),the aerial images taken by it can be greatly affineddeformed due to tilting and shaking of UAV.Therefore,it is very difficult to attain the good result by using conventional images mosaic algorithm.This paper details the images mosaic algorithm characterized with Scale Invariant Feature Transform (SIFT),which solves the problem of interference for great translational motion,rotation and scale variation between the images to be mosaicked by firstly extracting the scale invariant feature points of the images,then the initial matching feature points set is attained by means of Euclid's distance judgment,and further précised with RANSAC method so as to work out the accurate transformation matrix,finally the image blending technique in weighted average method is adopted to achieve the stable and robust image mosaic effect.

images mosaic,aerial image,SIFT,features matching

2011-11-15)