环状给水管网计算方法的研究
樊建伟
0 引言
随着我国经济建设的快速发展,城市日新月异,人民生活水平在不断提高。为此,工业用水量和生活用水量也迅猛增加,原有的给水系统已不能满足日益增长的需要,改建和扩建城市给水管网工作在不断地进行中。与此同时,国家建设部又制订了“供水行业2000年规划”,提出了两项提高(安全、效益)和三项降低(电耗、药耗、漏失)的目标,这对我国供水事业加强科学管理、提高服务质量、提高经济效益提出了更新的要求[1,2]。目前的管网多存在水力不平衡现象,有些管网虽然按照环状设计,但实际多按枝状网运行,不但没有发挥环状管网的优势,而且浪费了投资;有些管网按照标准管径进行管网的水力计算,不能满足回路压力平衡方程;还有些环状管网,随着运行的时间越来越长,其水力不平衡现象也越来越严重。其主要原因是我们对环状管网缺乏认识,设计、运行管理水平相对较低,计算环状管网的方法相对较少。因此,针对目前国内给水管网的这一现状,为配合城市建设,更好地对地下水管进行建设和维护,同时也利于自来水公司建设管网管理系统的需要。本论文在目前国内外给水管网水力分析算法的研究基础上,为充分发挥环状管网的优势,对环状管网进行了优化研究。
1 流体管网水力工况数学模型
在流体管网中,流体流动满足基尔霍夫第一、第二定律。
即:

其中,A,Bf分别为管网的基本关联矩阵和基本回路矩阵,若管网支路数为B,节点数为N+1,则A为B×N阶矩阵,Bf为(BN)×N阶矩阵;G,ΔH分别为支路流量列向量,支路两节点间压降列向量;Z为各管段支路中两节点的位能差列向量(B维);DH为管段支路的能量输入项列向量(B维),当管段不含能量输入项时,DH=0;S为B×B阶对角矩阵;Sj为各管段支路的阻力特性系数;|G|为B×B阶对角矩阵;|Gj|为各管段支路流量的绝对值。
上述方程组中,共有2B个未知变量(B个Gj,B个ΔHj),同时也有2B个方程,由A,Bf的性质可知,方程组中没有多余方程,故有唯一解。
2 基本关联矩阵和基本回路矩阵的形成[3]
2.1 基本关联矩阵的形成
以图1为例说明,通过分析发现,图1中管段号与节点号的关系可以用表1的方法表示。
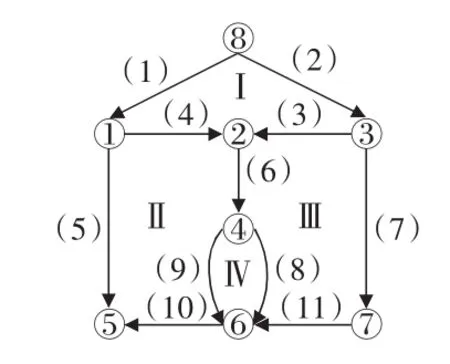
图1 网络拓扑图

表1 管段号和节点号表示方法
以表1第二行的某个值为行号,以该值的列号为A矩阵列号的值为1(表示起点);以表2,表3第三行的某个值为行号,以该值的列号为A矩阵列号的值为-1(表示终点),其余为0。
2.2 基本回路矩阵的形成
规定:对于每一条管段,沿着所设流动方向,在管段左边的环路号填入表2第二行相对应的位置,管段右边的环路号填入表2第三行相对应的位置。图1所示管网的管段与环路关系数组用表2表示。

表2 管段号与环路号表示方法
以上两矩阵形成可通过VC语言编程实现。
3 模型计算方法
供水管网的水力平衡计算是供水系统规划设计、经济评价和运行管理的基础,其主要目的就是在确定管径的情况下了解满足连续方程和能量方程的各节点压力水头和各管段的流量,为管网的科学管理提供信息资料,目前求解这些未知量的方法有解环方程法、环流量法,解节点方程法和管段流量法两种。在满足连续方程的条件下,用求解各环校正流量的方法,来间接解出各管段流量的方法叫解环方程法,也就是Hardy Cross法。以节点连续方程为基础,把方程中的管段流量通过管段压降计算公式,转化为用管段两端的节点压力表示,这样连续方程转化为满足能量方程,以节点压力为变量的方程组,通过求解方程组便可得各节点压力,此法称为节点法。管段流量法是将节点连续方程和环能量方程联立形成有p个独立方程的方程组,其个数为管网管段数,将其转化为以管段流量为变量的方程组,由于能量方程为非线性方程,难以直接求解。
经过比较,本文采用节点法计算[4],对管网进行水力计算,要求满足以下三个方程组:
1)节点流量连续方程组Aq+Q=0;2)管段压力降方程组ATP=Δp;3)管段流量方程组q=C·Δp。
由上述三式可得求解节点压力的方程组:

其中,A为由元素aij组成的节点关联矩阵;C为由元素1/Sj·qj组成的节点对角矩阵;P为节点压力向量;Q为节点流量向量;q为管段流量向量;Δp为管段压降向量;AT为矩阵的转置矩阵。
计算步骤:首先初设管段流量q(0),形成方程组(4),求解节点压力p(1),计算出q(1);q(1)不满足要求进行修正,再形成方程组(4)进行逐次逼近,直到第K+1次的q(K+1)与q(K)差的绝对值满足计算精度要求为止。
4 计算实例
如图2所示,供水管网有6个节点,7个分支,管网总流量为0.3 m3/s,按照节点流量平衡原理和选取的限定流速确定各管段的管径。
各管段的管长、管径和阻抗如表3所示。

图2 某供水管网

表3 管网原始数据
取迭代精度为0.000 1,把表3中数据代入程序进行计算,得计算结果见表4。

表4 管网计算结果
5 结语
本文提出了目前环状管网运行中普遍存在的一些问题,针对该问题,运用基尔霍夫定律建立数学模型,考虑各种算法的优缺点,选用节点法对环状管网进行了计算机编程计算。
[1]严煦世,赵洪宾.给水管网理论和计算[M].北京:中国建筑工业出版社,1986.
[2]许仕荣,邱振华.给水管网的计算理论与电算应用[M].长沙:湖南大学出版社,1997.
[3]彭继军,田贯三.燃气管网拓扑结构的计算机生成方法[J].山东建筑大学学报,2002,17(2):50-54.
[4]田贯三,张增刚,江 亿.城镇天然气管网水利分析数学模型与计算方法[J].天然气工业,2002,22(3):96-98.

