河南省2010年肾综合征出血热时间和空间聚集性分析

王海峰，尤爱国

肾综合出血热是由汉坦病毒引起，伴有肾损综合征的一组出血热的综合名称［1］。河南省于1963年首次报告肾综合征出血热病例，上世纪80年代经历过2次发病高峰，2次高峰发病人数均接近万例，此后疫情逐渐呈下降趋势［2］。但近年来，河南省肾综合征出血热疫情又开始小幅度回升。因此，搞清肾综合征出血热病例时空分布特点，对探索疾病流行因素，进一步指导防治肾综合征出血热工作具有较高的应用价值。本文将河南省2010年度肾综合征出血热报告病例数按日期和县区分布，分别进行Poisson分布和负二项分布的拟合，并进行检验，对病例的时间和空间聚集性进行分析。

1 材料和方法

1.1 疫情数据2010年河南省肾综合征出血热疫情资料来自“中国疾病预防控制系统V2.0”中的子系统“疾病监测信息报告管理系统”。

1.2 概率模型

1.2.1 Poisson分布［3］

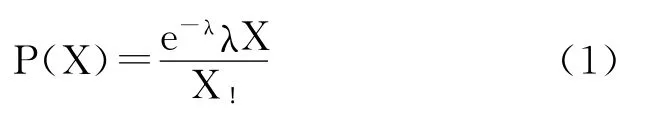
（1）式中，e为自然对数的底，e＝2.71828；λ为总体平均数，可用样本平均数代替。X为报告病例数，X＝0，1，2，3……n。计算出X对应的P之后，理论频数T X＝NP（X）。N为观察单位总数。

1.2.2 负二项分布［3］负二项分布的参数μ一般用样本均数作为其估计值，但参数k的估计就复杂一些。k值有4种估计方法［4］，本文先用矩法估计一个粗略的k值，然后再用最大似然法估算精确的k值。所谓矩法就是用样本的均数和方差S2分别作为负二项分布的均数μ和方差σ2的估计值，由下面式（2）求得。

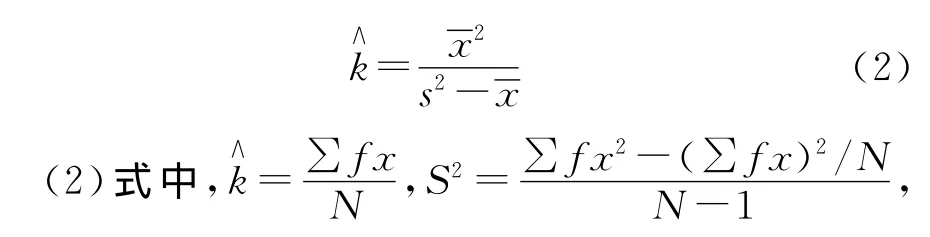
f为样本阳性数，X对应的频数，N为观察单位总数。

所谓最大似然法（maximum likelihood method）是指能够满足下面式（3）的Z＝0的k值即为所求。

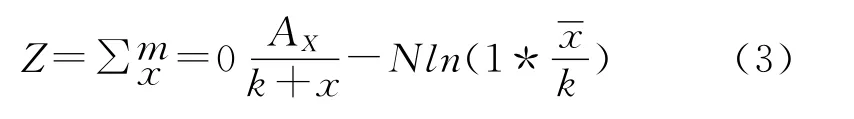
（3）式中m＝Xmax，即样本计数X所取得到的最大值；即样本中所有计数大于X的频数之和

求出精确k值后，令，则负二项分布的概率计算公式为

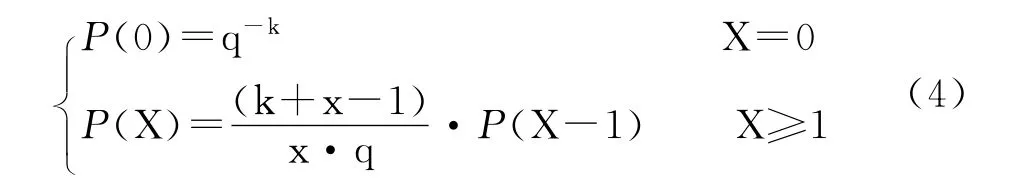
计算出X对应的P之后，理论频数T X＝NP（X）。N为观察单位总数。

2 结 果

2.1 发病概况 2010年河南省共报告肾综合征出血热病例186例。按天计算发病数，则254 d没有报告病例，其余每天发病数1～8例，每天平均发病数；按县区计算发病数，则分布在88个县区，每个县区病例数1～9例。有79个县区没有报告病例。每县区平均发病数

2.2 时间（日）分布与Poisson分布和负二项分布的拟合 按照X＝0，1，2，3……8，将一年365 d对应的实际频数进行归类计数（见表1）。根据式（1）计算X对应的Poisson分布概率，求出各组的理论频数T X；负二项分布则先由矩法求出粗略的k＝0.557 3，再由最大似然法求出精确的k＝0.561 3，根据（4）求出各组的理论频数T X。拟合优度检验用卡方检验。

由表1可看出，河南省2010年肾综合征出血热发病时间分布不服从Poisson分布（χ2＝51.251 9，v＝2，ν＝0.05，P＜0.05），而服从负二项分布（χ2＝0.414 3，v＝2，ν＝0.05，P＞0.05）。由此，可以认为河南省2010年肾综合征出血热病例在时间分布上不是随机均匀分布的，而是表现出一定程度的聚集性。用圆形分布法对2010年河南省肾综合征出血热进行季节性分析后，平均角（雷氏检验P＜0.05），所对应的高峰日期为11月14日。

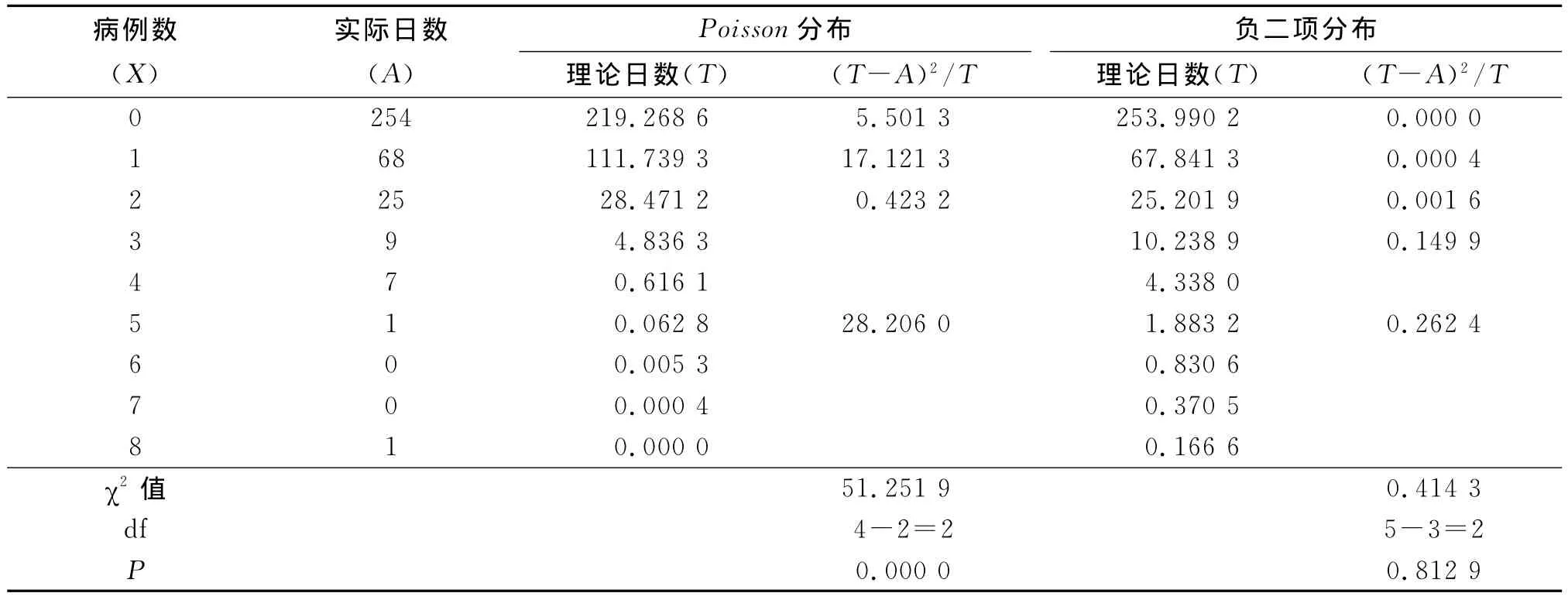
表1 河南省2010年肾综合征出血热时间（日）分布与Poisson分布和负二项分布的拟合Tab.1 The fitting on temporal distribution of HFRS cases in Henan Province in 2010 by Poisson distribution and negative binomial distribution

2.3 空间（县区）分布与Poisson分布和负二项分布的拟合 按照X＝0，1，2……9，将河南省167个县区对应的实际频数进行归类计数（见表2）。根据式（1）计算X对应的Poisson分布概率，求出各组的理论频数T X；负二项分布则先由矩法求出粗略的k＝0.740 9，再由最大似然法求出精确的k＝0.845 5，根据（4）求出各组的理论频数T X。拟合优度检验用卡方检验。

由表2可看出，河南省2010年肾综合征出血热发病空间分布不服从Poisson分布（χ2＝67.121 3，v＝3，ν＝0.05，P＜0.05），而服从负二项分布（χ2＝7.254 3，v＝3，α＝0.05，P＞0.05）。由此，可以认为河南省2010年肾综合征出血热病例在空间分布上不是随机均匀分布的，而是表现出一定程度的聚集性。结合流行病学标点地图，可以看出病例主要聚集性驻马店市的正阳县、平舆县和汝南县等地。

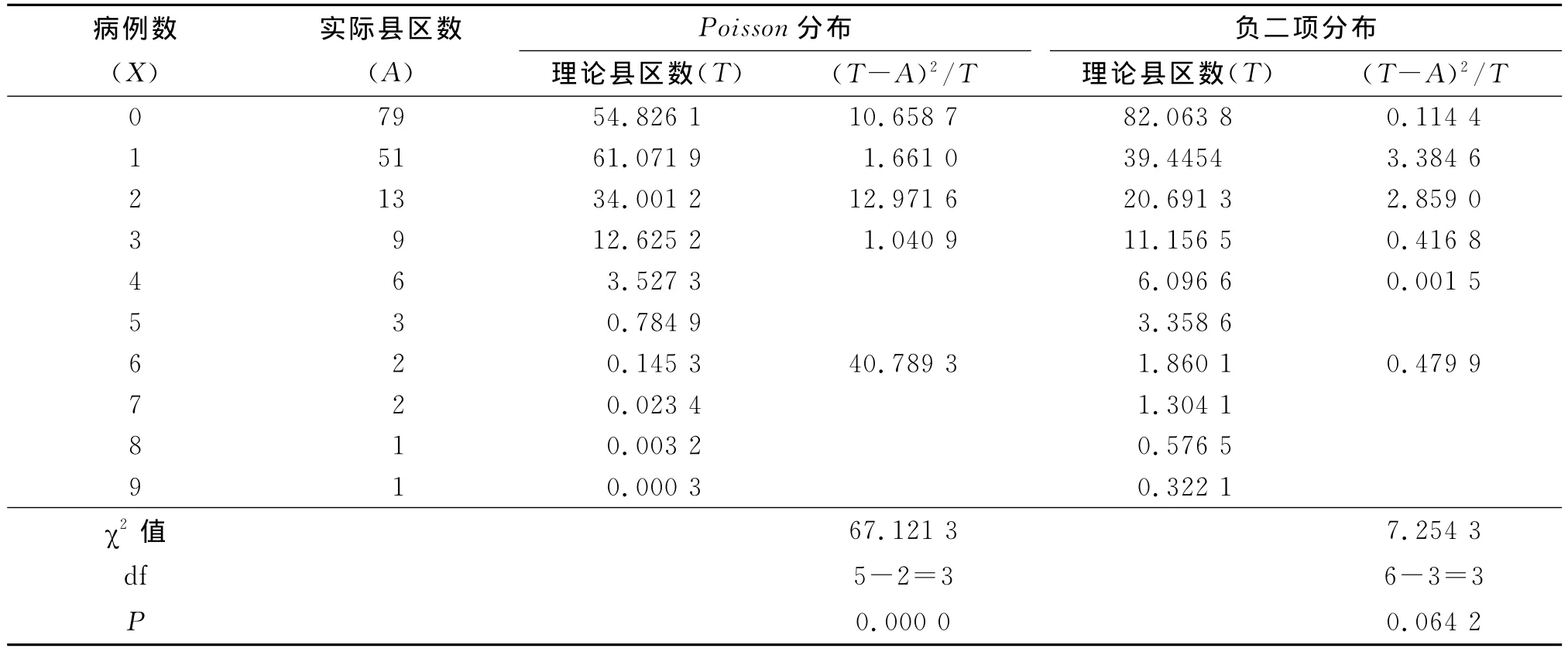
表2 河南省2010年肾综合征出血热空间（县区）分布与Poisson分布和负二项分布的拟合Tab.2 The fitting on spatial distribution of HFRS cases in Henan Province in 2010 by Poisson distribution and negative binomial distribution

3 讨 论

Possion分布是一种稀有事件的随机均匀分布，服从Possion分布的事件彼此间是相互独立的，如某人是否患某种疾病与他人是否患该病无关等；换言之，若不服从Possion分布，则可认为某一疾病等事件具有空间聚集性、传染性［5］。负二项分布是一种聚集性分布，在医学中主要用于聚集性疾病及微生物、寄生虫分布模型等的研究［3］，具体地说，当个体间发病概率不相等即可以拟合负二项分布，如单位人数内某传染病的发病人数等。肾综合征出血热是一种以鼠为宿主动物的自然疫源性疾病，其发病特点是自然散发。根据本研究结果，可认为2010年河南省肾综合征出血热病例在时间和空间分布上皆不服从Poisson分布，而皆服从负二项分布，这提示每个时间或空间单元内阳性个体的存在，受到了某些因素的影响，从而导致病例分布不再呈现随机、均匀的特点，呈现一定程度的聚集性。

郭凤莲［6］等对山东省莒南县1975－2004年的肾综合征出血热时空动态变化进行了研究，发现在肾综合征出血热流行初期，发病处于原始的自然散发状态，病例呈现Poisson分布。但是，随着自然疫源状态被破坏，肾综合征出血热病例分布开始服从负二项分布。导致这种变化的原因，薛付忠［7］等认为是在秋末冬初灭鼠的时候，由于只灭家鼠，不灭野鼠，破坏了家、野鼠之间的生态平衡，使得带病毒野鼠广泛向室内迁移，人群感染机会增大，形成秋末冬初峰。春天家鼠密度回升，与野鼠争夺领地，病毒在家野鼠之间传播，形成春末夏初峰。因此，对于服从负二项分布的疫源地，在制定灭鼠措施的时候要采取综合灭鼠措施，尽可能维持家鼠和野鼠之间的平衡，才有可能消除疫源地。

［1］宋干.肾综合征出血热［J］.预防医学论坛，2005，11（4）：508－512.

［2］李林红，吴振溢，张彦平，等.河南省肾综合征出血热不同类型疫区监测比较研究［J］.中国媒介生物学及控制杂志，2002，13（2）：127－130.

［3］孙振球.医学统计学 ［M］.2版.北京：人民卫生出版社，2007：124－131.

［4］查明.负二项分布参数K的四种估算方法［J］.热带病与寄生虫学，2000，（29）2：107－109.

［5］金丕焕.医用统计方法 ［M］.2版.上海：复旦大学出版社，2008：197.

［6］郭凤莲，许桂春，李学刚，等.山东省莒南县肾综合征出血热的空间分布及其时空动态变化［J］.中国预防医学杂志，2007，8（5）：559－562.

［7］薛付忠，王洁贞，马希兰.疾病空间分布状态的负二项分布概率生成模型的讨论［J］.中国卫生统计，2000，17（6）：366－368.