综合服务型物流企业的评价模型

周素静 李 静

(郑州铁路职业技术学院，河南 郑州 450052)

一、问题的提出

作为物流行业的行业组织或评级机构，往往需要对各个物流公司进行综合评价，以便引导行业的健康发展，并为相关行业、部门提供决策参考或咨询。

根据国家物流企业的分类和评估指标的有关规定，综合服务型物流企业的评估指标体系如下:

1.经营状况与资产:包括年综合物流营业收入和营业时间、资产总额和资产负债率四个二级指标;

2.设备设施:包括自有或租用仓储面积、自有或租用货运车辆和运营网点三个二级指标;

3.管理与服务:包括管理制度与质量、业务辐射面、物流服务方案与实施、顾客投诉率四个二级指标;

4.人员素质:包括中高层管理人员素质和业务人员素质两个二级指标，分别指中高层管理人员中具有大专以上学历，或行业组织物流师认证的比例、业务人员中具有中等以上学历或专业资格的比例;

5.信息化水平:包括网络系统、电子单证管理、货物跟踪、客户查询四个二级指标。

假设某物流行业评估机构组织专家对四个综合服务型物流公司P1，P2，P3和P4进行相关指标的评估和采集，专家们经过认真分析，从中选出主要的、有区别的一些指标如表1所示。试根据表1中的信息，对四个物流企业进行定量的综合评价，并进行排序。

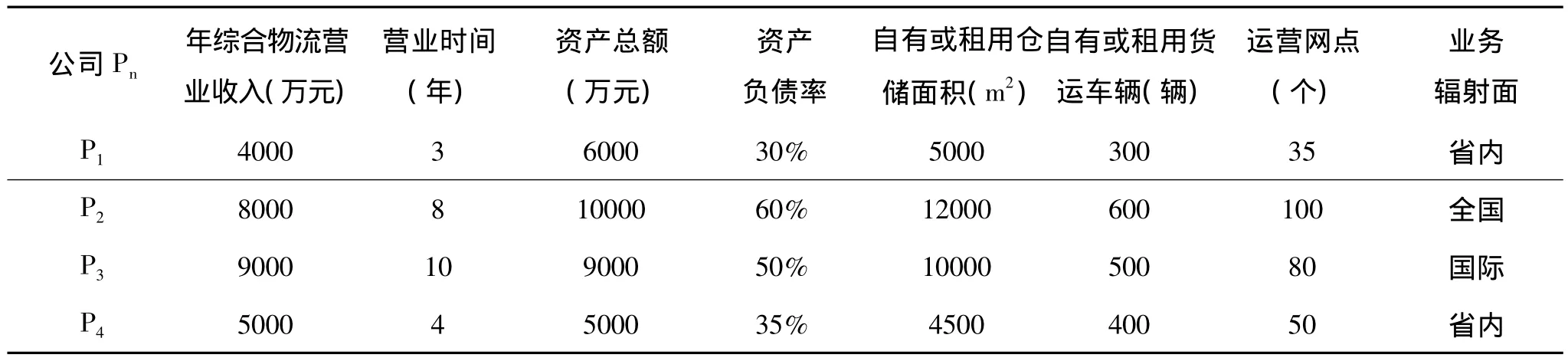
表1 四个物流公司的各项指标

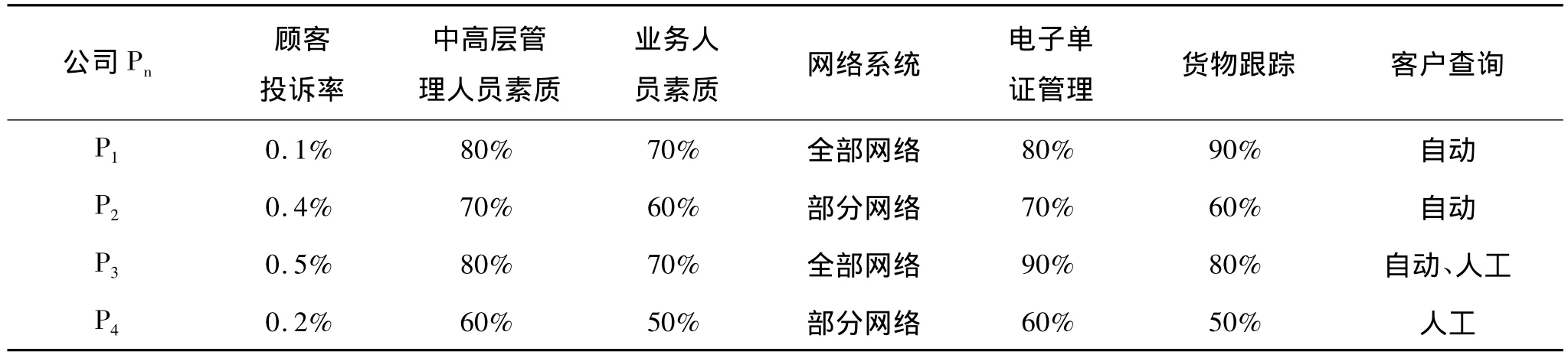
公司Pn顾客投诉率中高层管理人员素质业务人员素质 网络系统 电子单证管理 货物跟踪 客户查询P1 0.1% 80% 70% 全部网络 80% 90%自动P2 0.4% 70% 60% 部分网络 70% 60% 自动P3 0.5% 80% 70% 全部网络 90% 80% 自动、人工P4 0.2% 60% 50% 部分网络 60% 50%人工

二、模型的分析与假设

从表1可以看出，评价指标有定量的，也有定性的，四个公司各指标的值互有强弱，因此，这是一个定性与定量相结合的综合评价选优排序问题，可以利用层次分析法进行分析决策。

1.根据对相关专家及客户的调查，五个一级指标对综合评价的影响由大到小依次为经营状况与资产、设备设施、管理与服务、信息化水平、人员素质。

业务辐射面指标的量化方法:省内得分为1，全国得分为2，国际得分为3;

网络系统指标的量化方法:全部网络化得分为3，部分网络化得分为1;客户查询指标的量化方法:只有人工查询系统得分为1，只有自动查询系统得分为3，同时有人工和自动查询系统得分为5。

2.由于资产负债率和顾客投诉率越高对评价越不利，因此，需要把表1中这两个指标的数据进行处理。不妨设:

资产负债率指标的量化值=1－资产负债率;

顾客投诉率指标的量化值=1－顾客投诉率。

根据表1和上面的分析，表1中的指标量化值如表2所示。并给出如下的假设:

(1)对于表2中所列指标及相应量化值，四个物流公司均无异议，且能够反映它们的实力;

(2)五个一级指标对综合评价的影响由大到小依次为经营状况与资产、设备设施、管理与服务、信息化水平、人员素质，且相邻两个影响之差基本相同;

(3)二级指标的量化值是在广泛进行专家咨询及客户调查的基础上产生的。

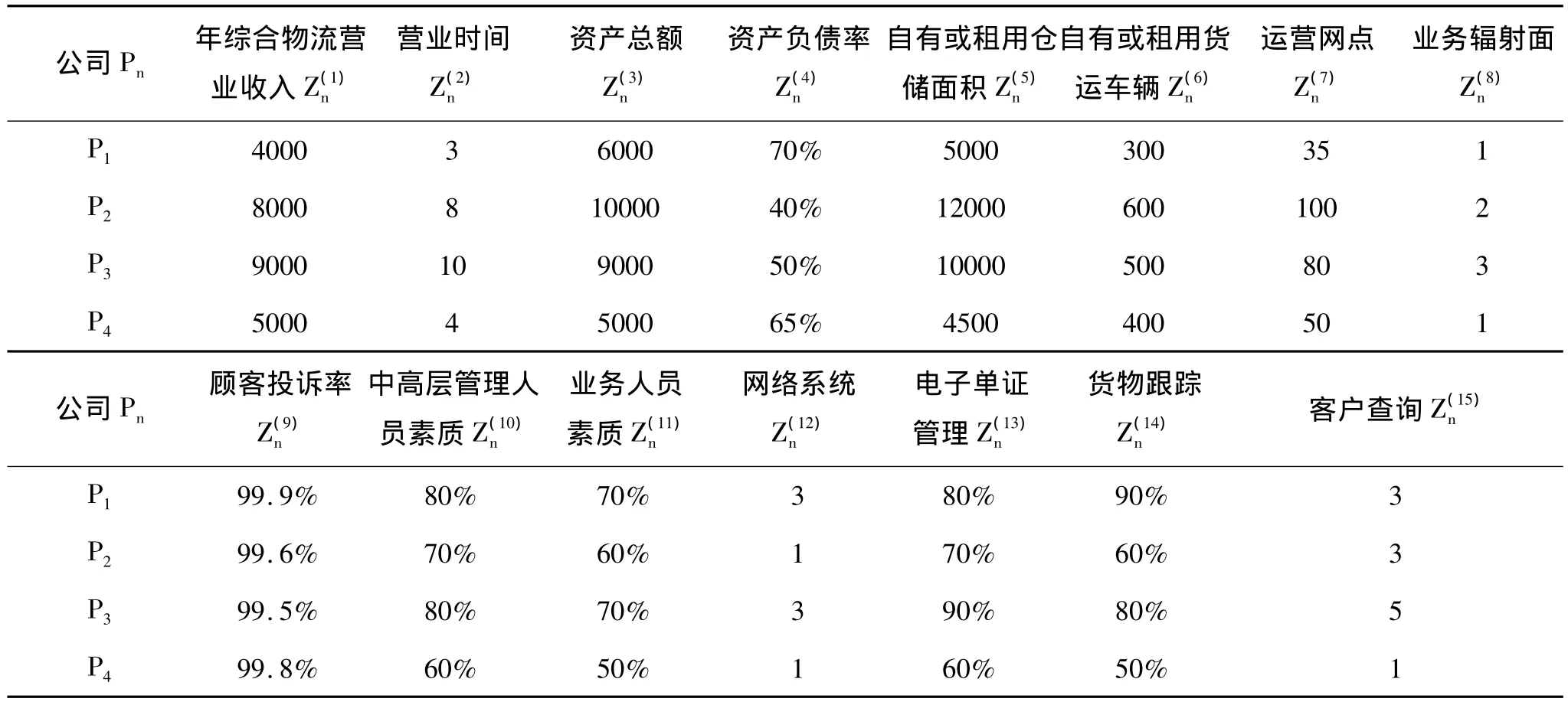
表2 四个物流企业的各项指标及量化值

三、模型的建立与求解

1.建立层次结构图

根据题目所给的各评价指标确定目标层O、准则层C、子准则层D和方案层P，建立如图1所示的层次结构图。

2.确定准则层C对目标层O的权重向量

根据前面假设，可以构造准则层对目标层的两两比较矩阵为

由和法计算可得最大特征根及对应的特征向量归一化分别为

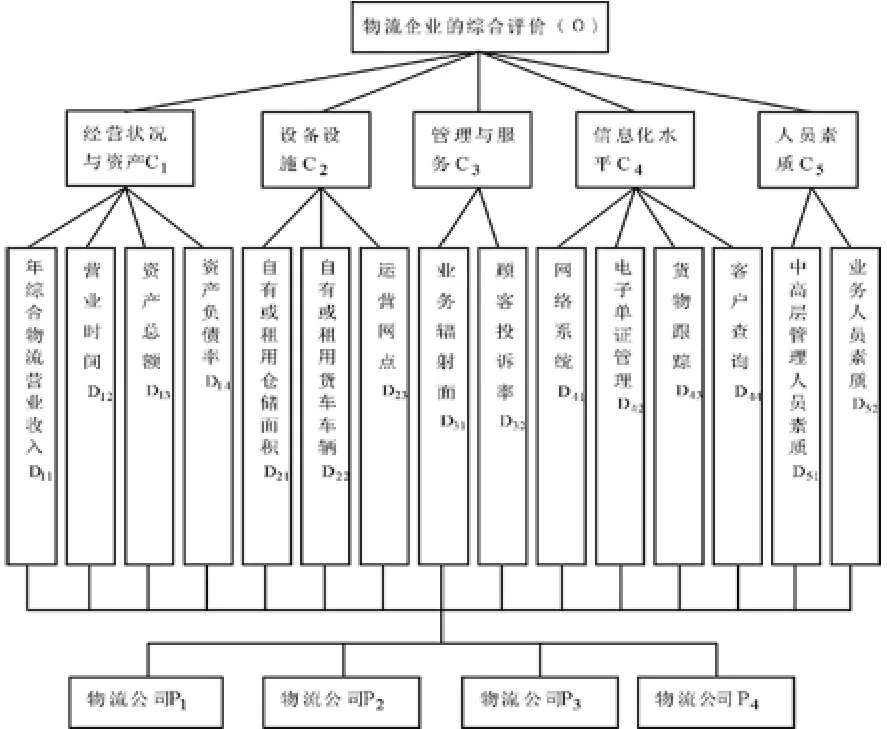
图1 物流企业综合评价的层次结构图

3.确定子准则层D对准则层C各因素的相对权重向量

通过咨询相关专家及客户调查，构造子准则层对准则层 C1，C2，C3，C4和 C5的两两比较矩阵分别为

用和法计算可得各矩阵的最大特征根和对应的特征向量归一化分别为

一致性检验:计算可得

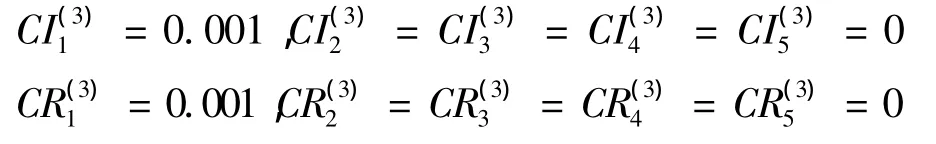
全部通过一致性检验。

子准则层15个因素对准则层各因素的相对权重向量分别为:

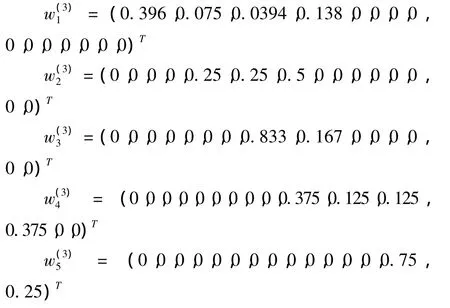
以它们为列向量构成的矩阵为

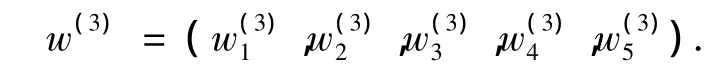
子准则层对目标层的组合权重为

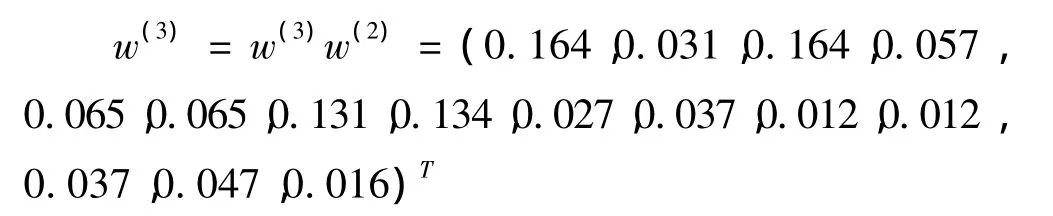
第三层对目标层的组合一致性检验:

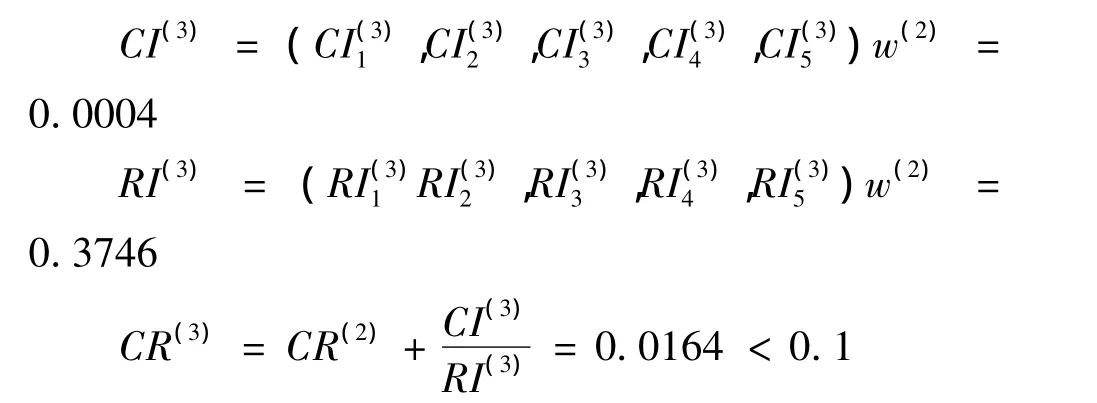
所以，第三层通过组合一致性检验。

4.确定方案层对子准则层各因素的相对权重向量

分别构造方案层中四个物流公司对子准则层中各因素的两两比较矩阵

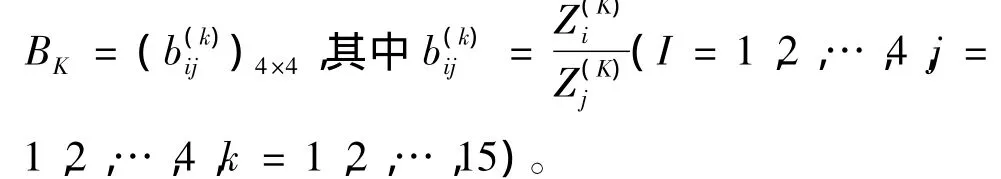
由矩阵BK(k=1，2，…，15)的构造可知，它们都是一致阵。由一致阵的性质可知，矩阵BK的最大特征根λk=4=0，将其任一列向量归一化后可得方案层对子准则层中因素Ck的相对权重向量(k=1，2，…，15)，以为列向量可得第四层对第三层的权重向量矩阵

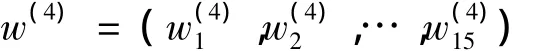
5.确定方案层对目标层的组合权重向量并进行综合排序

方案层对目标层的组合权重向量为

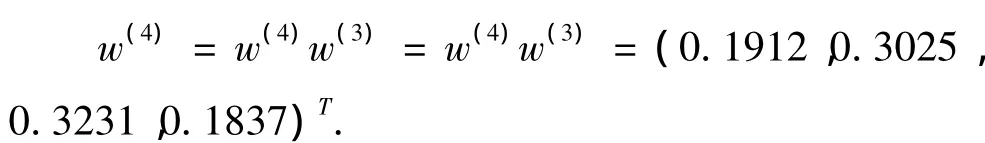
第四层对目标层的组合一致性检验:

第四层通过组合一致性检验，组合权重向量

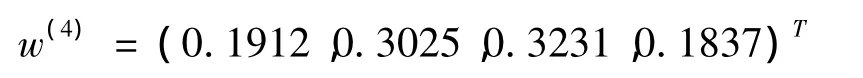
可以作为最终的决策依据.由此可以看出，物流公司P3的综合评价最高，实力最强，四个公司的实力由强到弱的排序结果为 P1，P2，P3，P4。

四、模型的结果分析与应用

1.本模型中采用的评价指标及相关数据均来自权威网站，层次分析过程中所构造的两两比较矩阵均是根据网络调查及专家群组判断的方法得到，有较高的可靠性，能够系统、公正、有效地评价综合服务型物流公司的综合实力。

2.该模型具有广泛的应用价值，还可以应用到其它类似的评价问题中，例如，优秀学生的评选问题、科技成果的综合评价问题、人才的录用问题等。

［1］姜启源，谢金星，叶俊.数学模型(第三版)［M］.北京:高等教育出版社，2003.

［2］韩中庚.数学建模方法及其应用(第二版)［M］.北京:高等教育出版社，2009.

［2］中国物流学会.中华人民共和国国家标准物流企业分类与评估指标.http://wenku.baidu.com /view/c9752a563 c1ec5da50e2707a.html