高频斯特林热声发动机的工质特性研究

邢乐乐 康慧芳 郑宏飞 江 钒 周 刚

(1北京理工大学机械与车辆工程学院 北京 100081)

(2中国科学院理化技术研究所低温工程学重点实验室 北京 100190)

1 引言

热声系统内的声振荡工质不仅是热能和声能传递与储存的载体，还是热声系统中产生热声效应的关键环节。热声发动机或制冷机中，声波使工质微团在热声回热器中经历一定的热动力学循环，在无运动部件的条件下实现了热能到声能的转换或泵热。热声效应的实现依赖于热声工质的声振荡，然而，热声学的研究工作［1-3］多集中在回热器水力半径、阻抗和相位等回热器结构参数和工作声场条件上，对热能和声能的存储、传递和转换的载体工质却缺乏详细系统的研究。

由于影响热声效应的参数的多样性和复杂性，只有少数研究者关注到了热声系统中声振荡工质的研究。1994年Giacobbe［4］给出了混合气体的普朗特数的计算方法，为热声系统的工质优化奠定了基础。基于Giacobbe的混合气体参数计算方法，1999年Belcher［5］研究了工质的比热容比和普朗特数对驻波型热声发动机起振温度的影响，他指出降低系统起振温度需要增大工质的普朗特数并减小工质的比热容比。1999年浙江大学金滔等人［6］基于线性热声学公式，探讨了工质在热声热机中的作用机理，指出热声效率的提高可通过选择具有低普朗特数的工质来实现。2002年Tijani［7］实验研究了普朗特数对热声制冷机性能的影响，他指出随着普朗特数的减小，热声制冷效应会增强。此外，何雅玲［8］等研究者通过改变热声热机中的气体工质，探索性的研究了几种气体工质对驻波型热声发动机性能的影响。

以上对热声热机的工质研究，均集中在理论或驻波机上，对高频行波型热声发动机的实验研究却显得较为缺乏。与驻波型热声发动机相比，行波发动机具有起振温度低、效率高等优点，因此得到了较快的发展。高频斯特林发动机作为一种新型的行波发动机和理想的压力波发生器，不仅结构紧凑、体积小，而且显著降低了系统的起振温度并提高了工作频率和压比。1999 年，Backhaus和 Swift［9］成功建造了第一台行驻波混合型热声发动机，其效率相对驻波机大幅提高。实验表明，当以氦气为工质时，该发动机的压比达到了1.22，相对卡诺循环效率高达42%，为行波发动机的发展奠定了基础。

有效地降低起振温度、提高压比是提高热声热机性能的关键，也是进一步优化其热力性能、提高热机效率的有效途径。工质的种类、充气压力、工作温度对系统的起振温度和效率有着较大的影响，因此对高频斯特林热声发动机的工质特性进行研究具有重要的意义。

2 实验装置与测试

本文使用的高频斯特林热声发动机系统主要由以下几部分构成:高频斯特林热声发动机、电加热装置、充气与抽真空装置、冷却循环水系统、数据采集系统。其中高频斯特林热声发动机由环形圈与谐振管两部分构成，其结构如图1所示。

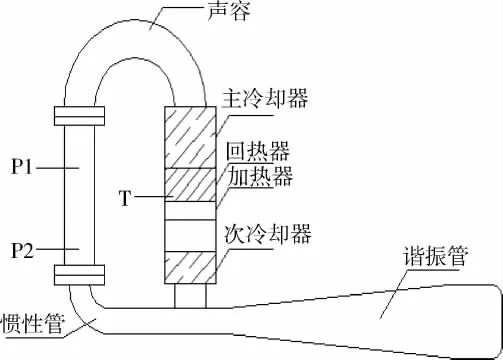
图1 高频斯特林热声发动机结构Fig.1 Structure of high-frequency thermoacoustic Stirling engine structure

实验中主要对压力与温度数据进行测试与分析，布置了2个压力测点与1个温度测点，分别为P1、P2和T。压力测点与温度测点分别位于环形圈中的反馈回路与加热器的高温端，其具体的测点位置可参见图1。实验中的压力数据采集系统由压力传感器、电荷放大器、信号处理器、数据采集卡、计算机等组成。温度数据采集系统由K型热电偶、UT70D型数字万用表、数据采集卡、计算机等组成。

3 实验结果与分析

3.1 起振温度分析

3.1.1 渗透层深度

实际工作的回热器中，在工质运动的垂直方向有两个重要的尺度，分别是热渗透层深度δk和粘性渗透层深度 δv，其定义如下［10］

式中:μ和k分别是气体工质的动力学粘度系数和热导率;ω为起振频率;ρm为气体的平均密度，cp为比定压热容。

以上两个特征尺度热渗透层深度和粘性渗透度表征的是气体振动周期除以π的时间内，热和动量在垂直于振动方向上扩散所能够影响的深度。在远大于这两个渗透层深度的地方，气体工质的运动和固体边界不存在热和动量的作用。当热声部件的横向尺度和热或者粘性渗透层深度在同一个数量级的时候，则气体的运动既要受到固体边界的热的影响，又要受到来自固体边界的粘性的影响。

回热器中对所经历的热声过程起决定性作用的是相对水力半径，它是回热器水力半径与热渗透层深度或粘性渗透层深度的比值，即:rh/δk和 rh/δv。相对水力半径综合考虑了回热器中热声转换过程所涉及到的固体通道和流体参数。对于不同工质的热声过程，行波热声发动机中存在最优的相对水力半径。由此，在热声热机回热器设计中需要根据热声系统所选用的工质特性选择合理的回热器水力半径，以实现最优的回热器热声转换。

由rh/δk和 rh/δv的表达式可知，可通过调整 rh(即丝网目数)和pm(即通过充气压力调整ρ)实现相对水力半径的变化。由于丝网目数调整工作的复杂性，主要通过调整pm来研究不同δk/rh或δv/rh条件下的气体工质对热声发动机起振温度的影响。

3.1.2 实验数据分析

由图2可知 CO2、He和 Ar在 0.6—3.0 MPa的充气压力内均可起振，而He起振的最低充气压力为1.2 MPa。当充气压力为1.95 MPa时，各种工质的起振温度接近一致，约为320℃。充气压力1.95 MPa可视为一临界点，在同一工况下，此处各种工质的起振温度趋于一致，而在此充气压力前后，起振温度呈现不同的变化趋势:当充气压力不高于1.95 MPa时，CO2的起振温度最低，且在相同的充气压力下He、Ar、N2和CO2的起振温度依次降低;当充气压力高于1.95 MPa时，He的起振温度最低。其中CO2、N2和Ar的起振温度曲线的基本变化趋势为:随着充气压力的升高而升高，而He起振温度曲线基本随着充气压力的升高而降低，CO2在0.8 MPa时达到最低起振温度258.3℃，N2在1.0 MPa时达到最低起振温度283.8 ℃，Ar在 1.0—2.2 MPa区间内的起振温度变化较小，在 1.0 MPa时达到最低起振温度330.2℃，He在 2.8 MPa时达到最低起振温度265.33℃。该特性为在高频斯特林发动机实验中选择合适的工质种类和充气压力以降低起振温度提供了实验依据。

图2 N2、He、Ar和 CO24种工质在不同充气压力下系统的起振温度曲线Fig.2 Influence on onset temperature of characteristics of working fluid under different pressures

根据图2中测得各个起振点，可以算得各个起振点所对应的热渗透层深度和粘性渗透层深度。在这个计算中，需要气体的温度T，系统的运行频率f，以及充气压力pm。回热器的换热过程和由此进行的熵波的调制的过程和回热器横截面的尺度是紧密相关的。直观的理解这个尺度不能过大，过大的回热器横向尺度使得整个回热器和气体工质之间处于一种不完全的热接触状态，气体所经历的热力学过程就是通常所谓的绝热过程。行波系统中通常要求的是良好的热接触和充分的热交换，而过小的回热器尺度会使得纵向的气体的流动的阻力大大增加。因此，存在一个最优的尺度，这是一个十分值得探讨的问题。另一方面，采用相对水力半径来分析是必要的。比简单的以水力半径、热和粘性渗透层深度来分析可靠性增加。为了分析的方便，采用回热器中纵向算术平均温度=(Tc+Th)/2作为计算温度。得到的热渗透层深度δk和粘性渗透层深度δv实际上是回热器纵向的平均值和。考虑到回热器作为系统的热功转换的核心部件，热功转换的是一种纵向的积分的效应，因而采用纵向平均的渗透层深度来进行分析是合理和可取的。

图3 起振临界温度差和r h/ 和 r h/之间的关系Fig.3 Relationship of onset temperature and relative hydraulic radius

图3 所示为起振临界温度差和rh/和 rh/之间的关系的曲线，这种曲线正是Rott最早提出的稳定性曲线形式。由图3可以发现，受工质特性的影响，4种工质起振温度的变化随着相对粘性渗透层深度的增大而不同。He呈增大趋势，而CO2、Ar和N2呈现先减小后增大的趋势并且存在极小值点。虽然4种工质特性不同，起振温度随相对水力半径的变化也不同，但是其最优rh/相差不大，其中CO2和N2为0.22，He和 Ar为 0.2，因此本系统中回热器中最优 rh处在 0.2—0.25 之间。rh/对起振温度的影响与 rh/类似，如图3所示，其中最优点对应的/数值略有增大，其中CO2和N2为0.26，He和Ar为0.24。因此本系统中回热器中最优rh/处在0.25 左右。

3.2 振荡压力幅值分析

3.2.1 操作因子

操作因子［11］ψ是由回热器相对长度和回热器温度分布决定的一个无因次参数，其定义为:

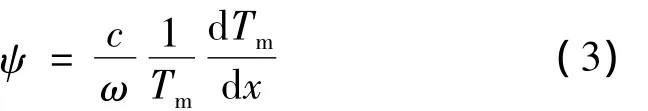
其中:c为声速;ω为角频率;Tm为回热器的温度;为回热器中沿x方向的温度梯度。当回热器内无二次流损失(即回热器的温度分布呈线性分布)时，ψ可近似为:

其中:lN=lreg/λ，lN为回热器的无因次长度，lreg为回热器的长度，λ为波长，Th为回热器中高温端温度，Ta为回热器中室温端温度。

操作因子是热声热机中回热器的一个重要参数，操作因子数体现了回热器长度和温度分布，使得回热器长度和温差的优化设计更为便捷。

3.2.2 实验数据分析

实验中，lreg=20 mm，λ =1.737 m，lN=0.011 5，Ta=291 K，发动机回热器高温端温度Th维持的稳定工况分别为:573、623、673、723、773、823 K，将以上数据代入式(4)，从而相应得到不同的ψ值:9.04、10.06、10.97、11.80、12.55、13.23。

图4 分别为 p2点处充气压力在 0.6、1.4、2.2 和3.0 MPa时操作因子对各种工质的压力振幅的影响。

如图4所示，在不同的充气压力下，各种工质的压力振幅均随着操作因子的增大而增大，各种工质的变化趋势基本一致，并且呈线性关系。增大操作因子能显著提高热声发动机的压力振幅。操作因子的大小由回热器的无因次长度和回热器的冷热端温度决定，因此减小回热器的长度和改变其两端温度差是增大操作因子的有效途径。在热声发动机确定和室温不变的条件下，回热器的无因次长度和冷端温度维持恒定，因此ψ的大小基本由回热器的高温端温度即Th决定，并且ψ值随Th的增大而增大。因此提高Th有利于热声发动机的驱动。对于同种工质在相同操作因子的情况下，压力振幅随着充气压力的增大而增大。如CO2在充气压力为0.6 MPa和3.0 MPa，操作因子为9.04时的压力振幅分别为0.312 5 MPa和2.329 1 MPa。因此，提高充气压力能显著提高热声热机的压力振幅。在相同的充气压力和操作因子下，CO2、Ar、N2、He 的压力振幅依次降低，而 He 在低压下无法起振。如在充气压力为2.2 MPa，ψ=10.06时，CO2、Ar、N2、He 的压力振幅依次为 1.81、1.65、1.60、1.40 MPa。因此 CO2具有较好的起振特性，是一种良好的工作介质。此数据为高频斯特林发动机工质的选择提供了实验依据。

图4 在不同的充气压力下，各种工质的压力振幅均随着操作因子的变化Fig.4 Influence on pressure amplitude of operation factor under different pressures

总之，提高充气压力、增大操作因子以及选用良好的工作介质，是提高高频斯特林热声发动机压力振幅的有效途径。

4 结论

本文搭建了一台高频斯特林热声发动机，并对其工质特性进行了实验研究。主要内容为N2、He、Ar和CO24种工质在不同充气压力下起振温度的变化，并引用了无量纲参数—操作因子和相对水力半径，分别研究其对压力振幅和起振温度的影响。通过实验分析可知:

(1)不同工质的起振温度曲线随充气压力的升高有不同的变化趋势。CO2、N2、Ar的起振温度均有个极小值，而He在低压下无法起振，其起振温度随充气压力的升高而降低。当充气压力不高于1.95 MPa时，CO2的起振温度最低，最低起振温度为258.3℃;当充气压力高于1.95 MPa时，He的起振温度最低，最低起振温度为265.33℃。

(2)操作因子作为一个无因次参数，对系统的压力振幅有着重要影响。各种工质的压力振幅均随操作因子和充气压力的增大而增大。其中CO2的压力振幅最大，在充气压力为3.0 MPa，ψ=13.23时达到最大压力振幅3.41 MPa。然而较高的操作因子和充气压力要求高频斯特林热声发动机具备更高的耐温特性和承压特性，并且长时间的高温工作对发动机的寿命也有一定的影响。

(3)相对水力半径对各种工质起振温度的影响不同，但最低起振温度对应相近的最优相对水力半径，以此最优区间设计回热器，对降低系统的起振温度具有指导意义。

1 Backhaus S，Swift G W.A thermoacoustic-Stirling heat engine［J］.Nature，1999，399:335-338.

2 Biwa T，Tashiro Y，Mizutani U.Experimental demonstration of thermoacoustic energy conversion in a resonator［J］.Physical Reviewe，2004，69(6):066304.

3 Gaelle P，Bertrand L.Optimal acoustic fields in compact thermoacoustic refrigerators［J］.Applied Acoustics，2007，68:642-659.

4 Giacobbe F W.Estimation of Prandtl numbers in binary mixtures of helium and other noble gases［J］.Journal of the Acoustical Society of American，1994，96:3568-3580.

5 Belcher JR，Slaton WV，Raspet R.Working gases in thermoacoustic engines［J］.Journal of the Acoustical Society of American，1999，105:2677-2684.

6 金 滔，陈国邦，应哲强.混合工质在热声制冷中的作用机理［J］.低温与超导，1999，27(1):37-42.

7 Tijani MEH，Zeegers JCH，Waele TAM.Prandtl number and thermoacoustic refrigerators［J］.Journal of the Acoustical Society of A-merican，2002，112(1):134-143.

8 Shen C，He Y L，Li Y G.Performance of solar powered thermoacoustic engine at different tilted angles［J］.Applied Thermal Engineering，2009，29:2745-2756.

9 Backhaus S，Swift G W.A thermoacoustic Stirling heat engine［J］.Nature，1999，399:335-338.

10 Swift G W.Thermoacoustics:A unifying perspective for some engines and refrigerators.Fifth draft［DB/OL］.http://www.lanl.gov/thermoacoustics，2004.

11 康慧芳.高频行驻波型热驱动热声制冷机的理论及实验研究［D］.北京:中国科学院理化技术研究所，2009.