开挖降水条件下基坑周围建筑物沉降预测研究

李 云 张建俊

基坑工程在开挖和排水过程中，由于基坑支护对地基土的扰动和排水造成的地基土固结作用，周边建筑物会发生一定程度的沉降，沉降量在允许范围内可视为正常现象，不会影响建筑物的正常运营与使用［1］。但如果超过允许限度，建筑物的安全与稳定将会受到威胁。因此对基坑周围建筑物进行定期定点监测，并在此基础上对未来可能发生的危害做出及时准确的预报是十分必要的。

针对以上这些情况，本章将引入优化组合单一预测模型进行预测的思想，即依据预测结果与实测值的符合程度利用一定的方法将不同的预测模型数进行优化加权组合，逐步建立能够准确预测建筑物沉降的组合预测模型，并经过实测值检验修正以至完善。

1 组合预测方法分析

1． 1 等权平均法

等权平均组合预测方法(EW方法)也就是对单一预测结果求和平均的组合预测方法。

设fi(i=1，2，…，k)为第i个模型的预测值，fc为组合预测值，则EW方法得到的组合预测值为:

EW方法只要求单一方法的预测值之间误差方差相近，对单一预测值fi的预测精度，以及单一预测结果误差之间的相互关系不予考虑。因此，只要预测值足够接近，EW方法就足够合理。

1． 2 最优加权法

记et=yt-ft为组合预测方法的预测误差，则:

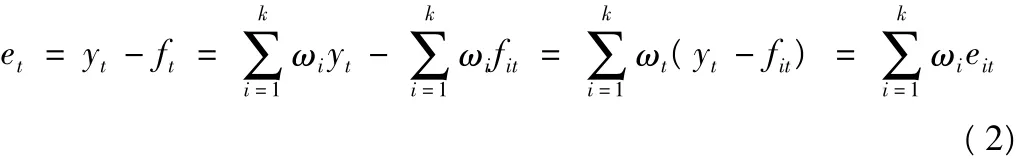
其中，yt为实际观测值，t=1，2，…，N;fit为第 i种方法的预测值;eit为第 i种方法的预测误差，eit=yt-fit(i=1，2，…，k);ωi为第i种方法的加权系数，且均预测值，即组合预测方法的预测

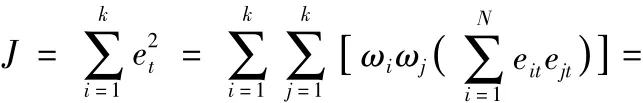
记组合预测方法的加权系数向量为 ω =［ω1，ω2，…，ωk］T，第i种预测方法的预测误差为 Ei=［ei1，ei2，…，eiN］T，预测误差矩阵为e=［E1，E2，…，Ek］，则组合预测方法的预测误差和J也可以表示为:

记 Rk=［1，1，…，1］T，则可以改写为ω=1。利用组合方法预测建筑物沉降的目的主要是减少预测值与实测值之间的误差，提高预测精度。如果存在一加权系数向量，可使组合预测模型的预测结果与实测值之间的误差平方和J达到极小值，则称ω为最优加权系数向量，此时所对应的组合预测模型即为最优组合预测模型。组合预测的最优权重求解，是对误差平方和在最小二乘准则下的数学规划问题:

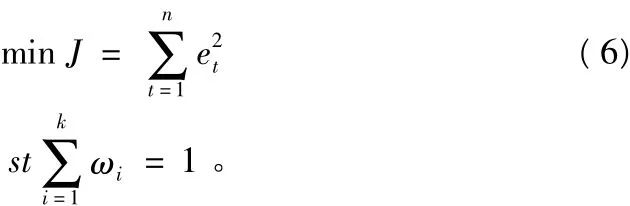
即:

对上式用拉格朗日乘子法求解，可得到:

目标函数的最小值为:

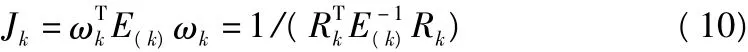
1． 3 递归等权法

使用递归等权法组合n种单一方法的基本思路如下:

1)简单平均组合n种单一预测方法，获得新模型;2)利用1)中获得的新模型替换原有n种单一预测方法中预测结果与实测值误差平方和最大的那个，从而获得新的n种单一预测方法(其中n-1种为原有预测方法);3)重复步骤1)和2)，直到预测误差平方和改进不大或达到预先要求的目标为止。

2 算例分析

阜新大众街地下商场基坑的施工，一定程度上对周边建筑物的稳定性造成影响，因此，针对周边建筑物合理布点监测，并对相应危害进行及时预报是信息化施工的关键。检测项目中，对A楼布设了13个监测点共进行了33期沉降监测。首先取前27期的沉降实测数据分别建立Gompertz曲线模型、灰色理论模型和BP神经网络模型，之后利用后期数据对预测进行检验，逐步建立组合预报模型，比较各种单一预测模型和组合预测模型的优劣(见表1和表2)。

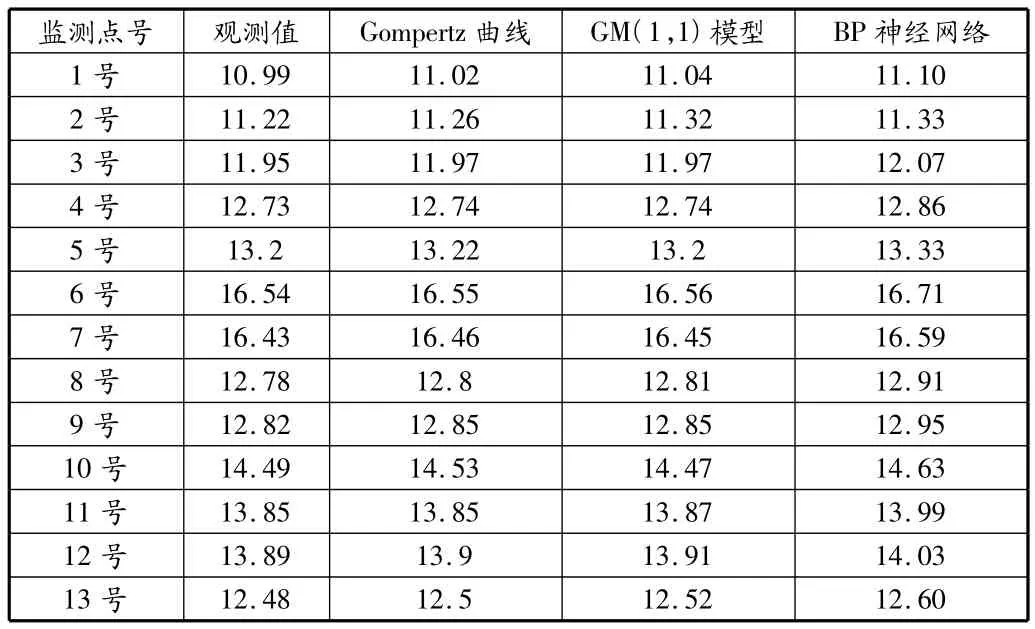
表1 单一预测方法的预测值 mm

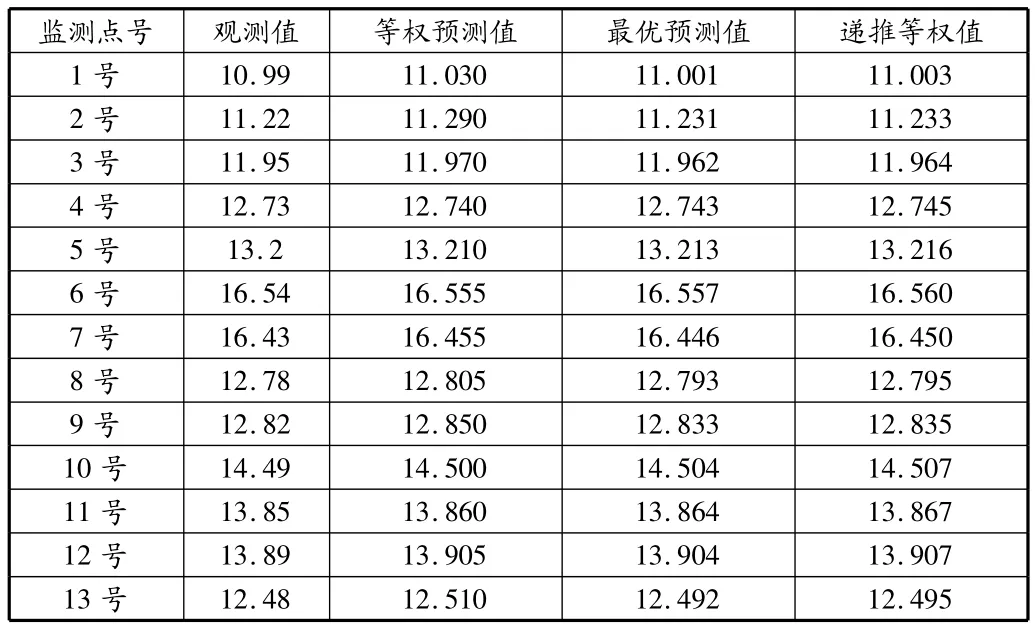
表2 组合模型预测值

表1，表2是通过前文所述三种不同组合优化方法组合预测的结果，比较分析误差情况得出单一预报模型最优组合的权重为:ω1=0．314 52，ω2=0．329 68，ω3=-0．350 93。表 3 列出了单一模型和不同组合模型预测结果与实测结果的误差平方和(SSE)、平均绝对误差(MAE)、均方误差(MSE)、平均绝对百分比误差(MAPE)、均方百分比误差(MSPE)，这些数据可以作为考察模型预报精度和可靠度的依据。

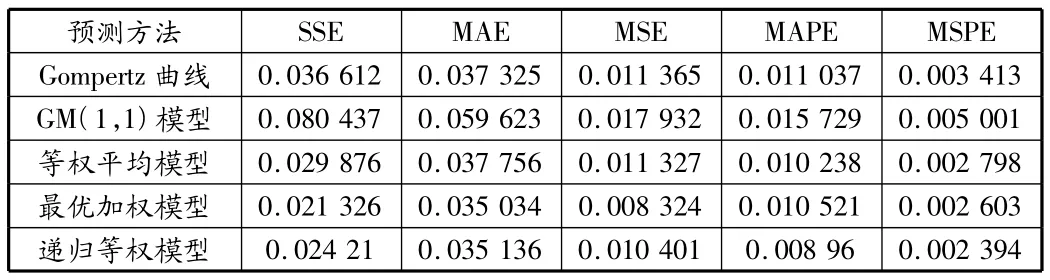
表3 不同预测方法的精度比较

3 结语

1)组合预测模型的精度明显优于单一预测模型预测的结果，说明组合模型预测的结果更加贴近实际，可靠度更高;2)简单求和平均的等权组合模型，计算方法简单快捷，公平对待每一个单一模型，在提高预测精度的同时，有效避免了外在因素的干扰。但预测精度略低于最优加权方法和递归等权方法;3)递归等权模型利用简单平均组合的高精度新模型替代低精度的旧模型，依次循环迭代多步，直至达到预期精度为止，使得精度比单纯等权平均模型有了进一步提高，在三种优化组合模型中预测精度居中;4)以预测结果与实测值误差平方和最小为约束准则的最优加权模型，由于是目标约束条件下的最佳优化组合，其预测精度最高，A楼最终预测结果为平均沉降13．349 5 mm。

［1］ 夏才初，潘国荣．土木工程监测技术［M］．北京:中国建筑工业出版社，2001．

［2］ 成 伟，陈建兵．高层建筑物沉降监测数据综合分析的几种方法［J］．地矿测绘，2004(20):1-3．

［3］ 汪树玉，刘国华．观测数据分析中几种方法的探讨［J］．水电自动化与大坝监测，2003(1):6-43．

［4］ 成 伟．高层建筑物沉降监测数据综合分析的几种方法［J］地矿测绘，2004(2):1-3．

［5］ 王立新．岩土工程监测数据统计分析方法应用技术［J］．公路运输文摘，2004(7):51-52．

［6］ 张正禄，张松林．大坝安全监测、分析与预报的发展综述［J］．大坝与安全，2002(5):6．

［7］ 贺可强，王胜利．神经网络法在深基坑变形实时预报中的应用研究［J］．建筑技术开发，2008，29(7):28-30．

［8］ 张庆华，陈爱云．神经网络在深基坑监测中的应用［J］．安全与环境工程，2004，11(2):8．

［9］ 方 兴．小波分析及其去噪性能研究［J］．浙江师范大学学报，2003，26(4):345-349．

［10］ 夏乐天，朱永忠．工程随机过程［M］．南京:河海大学出版社，2000．