基于有限差分法的岩溶地基稳定性研究★

陈海旭 罗爱忠

0 引言

我国的岩溶分布比较广泛，几乎占了整个国土面积的1/3。在岩溶地区，由于岩溶的作用，在建筑物或构筑物的地基中分布了大量的地基基础的稳定和变形影响较大的溶洞［1］。在利用岩溶地基作为上部建筑物或构筑物地基基础的持力层时，岩溶地基基础的稳定性就变得非常的关键。在对岩溶地基基础稳定性的评价中，大部分都是在现有自然条件下对岩溶的塌陷进行评价。对于岩溶地基稳定性的评价，当前的评价方法一般可以分为定性和定量评价两种，定性评价主要依靠设计施工者的工程经验，定量的评价主要有理论计算和数值计算两种方法［2-4］。数值计算的方法虽然比较繁琐，但精度相对较高。本文拟通过强度折减法与有限差分法数值计算相结合的方法，定量的评价岩溶地基顶板的稳定性。

1 岩溶地基稳定性分析评价

在评价岩溶地基的稳定性时，除了考虑岩溶围岩的物理力学性质，还必须了解工程建设场地的岩溶构造发育情况、岩体结构面的特征、溶洞的形态、顶板所承受的荷载及其他可能出现的人为因素等。它们与溶洞围岩的物理力学性质一样，都可以作为岩溶地基稳定性分析评价的重要依据。这些因素中，对于岩溶地基稳定性的影响各不相同。

1． 1 岩溶发育情况

岩溶的发育情况不仅包括了围岩岩体的断裂构造、褶皱构造等，还包括了特定的地质及水文地质条件，因为这决定了用于计算的地质概化模型的建立［5］。总体上来说，断裂构造的存在，为水的流通和载荷作用下的滑动提供了条件，它对岩溶地基的稳定性是不利的。它的力学性质、规模、岩体本身的胶结特征、断裂的发育程度等在一定程度上决定了上部构筑物地基的稳定性。张性和扭性断裂不利于地基的稳定性，压性和压扭性断裂对地基的稳定性影响较小。褶皱构造的存在，使得溶洞的围岩内分布了一定的节理，这有利于地下水的活动，对于岩溶地基的稳定性也是不利的。

1． 2 结构面和溶洞形态

在进行岩溶地基的稳定性分析时，结构面的性质、成因、空间分布及组合形态，是决定岩溶地基稳定性的重要因素。另外，溶洞的形态对岩溶地基的稳定性影响也较大，溶洞埋藏较深、覆盖层较厚、洞体较小都是对岩溶地基稳定性有利的因素;单体分布的溶洞及圆形溶洞同样有利于岩溶地基的稳定性。因此，在本文中采用最不利的矩形溶洞进行分析。

2 岩溶地基稳定性分析方法

2． 1 FLAC3D有限差分的基本原理

FLAC3D软件是一种显式有限差分程序，它的优点主要在于时步小于稳定时的临界值，每一时步只需少量的计算。FLAC3D在求解时采用了有限差分、空间离散及动态求解技术。先将分析域离散为由四面体单元组合形成的五面体或六面体单元，在显式时间差分求解中所有的矢量参数(力、速度和位移)均存储在网格节点上，所有的应力及材料特性均存储在单元的中心位置。通过运动方程由应力及外力可求出节点的速度及位移，再由空间导数得出单元应变率，借助于材料的本构关系，由单元应变率可获得单元新的应力。

2． 2 强度折减法

强度折减法是Zienkiewicz等在1975年首次在土工弹塑性有限元数值分析中提出了抗剪强度折减系数的概念，它的基本原理是将岩土体的强度参数c，φ同时除以一个折减系数Fs，得到一组新的参数值c'，φ'，然后作为新的材料参数代入程序进行计算，通过不断地变化折减系数Fs，直到顶板达到临界破坏，对应的折减系数即为安全系数。

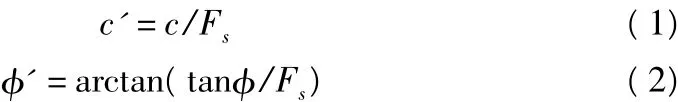
2． 3 顶板破坏的判定标准

强度折减法最初是用来进行边坡稳定性分析，它采用的是计算过程中计算不收敛作为破坏标准，也即是在一定的指定收敛标准下不收敛。在这种情况下，在不收敛时土体内的应力一般是不能满足破坏准则和总体平衡的要求的，因此采用不收敛作为破坏标准在物理意义上不是十分明确，这同时也是许多学者至今还对强度折减法持怀疑态度的原因所在。本文拟通过一定的经验和试算工作，采用土体内某一幅值的广义剪应变在土体内的贯通作为土体临近破坏的判定标准，寻找塑性区内潜在的滑移带贯通作为判别标准，其物理意义比较明确，计算图形形象清楚，能很好的作为顶板失稳的判别标准。在求解顶板的安全系数时，采用二分法的优化理论进行优化。

3 岩溶地基顶板稳定性分析计算

3． 1 基本假定

为了计算的简便，对岩溶地基的溶洞做如下的假定:

1)溶洞在天然状态下是稳定的;

2)溶洞围岩是均质的各向同性的，变形属于小变形;

3)溶洞内的充填物在分析时作为有利因素考虑，所以溶洞在计算时按空溶洞进行计算;

4)溶洞的形状和大小只考虑其现状，形状按长方体考虑，并将小型的群溶洞等效为单跨溶洞考虑。

3． 2 计算步骤

基于上面的基本假定，分为以下几个步骤:

1)调查计算工程施工段的地下空区分布，并进行合理的等效;

2)根据地下空区的分布和合理等效建立几何计算模型;

3)计算当前空区地面所承受的荷载大小，包括静荷载和动荷载;

4)进行自重应力作用下的静力场;

5)计算空区顶板安全系数;

6)确定顶板的稳定性。

如果计算出的安全系数不能满足安全需要，需要从第二步开始重复以后的步骤，直到达到给定的安全系数为止。

3． 3 计算参数

在计算中，计算力学参数采用下列值进行计算，具体数据如下:围岩重度为20 kN/cm3，弹性模量取18 GPa，泊松比为0．19，粘聚力取45 kPa，内摩擦角为30°。

3． 4 计算模型

以FLAC3D为平台，建立了岩溶地基的分析模型。岩溶围岩的应力应变关系特性考虑为理想弹塑性，采用摩尔—库仑屈服准则。如图1所示，模型在x方向取40 m，y方向取1 m，z方向取20 m。分析模型采用四面体网格，共有单元1 888个，节点3 976个。模型地面和侧面采用反向约束，表面自由。划分单元时，对于不同部位的单元，采用不同的大小，对于应力和位移情况需要了解得比较详细的部位或应力及位移变化比较剧烈的部位，单元应划得小一些，对于次要的部位或应力及位移变化比较平缓的部位，单元就可大一些。在溶洞顶板部位和承受外部荷载的部位，单元最小，在计算区域的边缘部位及底部，单元最大。从重要部位到次要部位，单元由小到大逐渐变化。

图1 几何模型

4 计算结果分析

4． 1 溶洞跨度与安全顶板厚度的关系

假定条形基础的荷载为0．5 MPa，顶板安全系数为1．3和1．4时，根据顶板塑性区分布，判断塑性区的分布是否贯通，根据前面定义的顶板破坏准则，得到跨度与顶板厚度的关系，见图2。

图2 溶洞跨度与安全顶板厚度的关系

通过对图2的分析，随着溶洞跨度的增大，达到相同的安全系数所需要的顶板安全厚度也相应的增大，它们之间满足如下的关系:

其中，Hsaf为岩溶顶板安全厚度;D为溶洞跨度;a，b均为材料系数，它与岩溶溶洞围岩的物理力学性质及所需要的安全等级有关。在本文中，对于顶板安全系数为1．3和1．4时，它们的取值见表1。

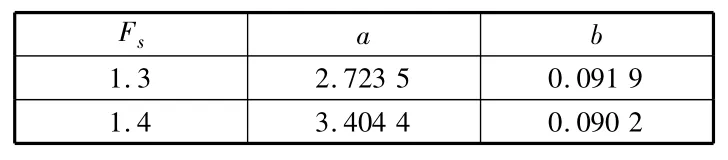
表1 材料系数取值

4． 2 溶洞顶板厚度与承载力的关系

计算了溶洞跨度为4 m，条形基础宽度为1 m时的顶板厚度与地基承载力的关系。此时，顶板的安全系数取为1．3。根据上面的顶板稳定的破坏准则，得到了顶板厚度与地基承载力的关系见图3。

图3 溶洞顶板厚度与承载力的关系

通过分析，随着顶板厚度的增大，地基的承载力相应的增大，它们之间满足如下的关系:

其中，c，d均为材料系数，它与岩溶溶洞围岩的物理力学性质及所需要的安全等级有关。本文中它们的取值为:c=0．353 5，d=0．125 2。

4． 3 溶洞跨度与承载力的关系

本文计算了顶板厚度为4 m，顶板安全系数为1．3时，不同跨度与地基承载力的关系。同样，采用上面的顶板稳定的破坏准则，得到了顶板厚度为4 m时，溶洞跨度与地基承载力的关系见图4。

图4 溶洞跨度与承载力的关系

通过分析，随着跨度的增大，地基的承载力相应的减小，它们之间满足如下的关系:

其中，e，f均为材料系数，它与岩溶溶洞围岩的物理力学性质及所需要的安全等级有关。本文中它们的取值为:e=7．720 3，f=0．207 9。

5 结语

通过岩溶条件下条形基础地基稳定性的定性和基于有限差分法与强度折减法结合的定量评价，得到了岩溶顶板厚度、溶洞跨度、地基承载力之间的定量关系，计算结果对于指导岩溶地区的岩溶基础设计和施工具有重要的意义。它们之间的关系表明，采用塑性区连通形成潜在滑移通道作为岩溶顶板破坏的判别标准物理意义明确，并且可以在一定的安全系数条件下，求取岩溶顶板破坏的临界厚度;在一定的岩溶顶板厚度条件下，得到作用建筑物后地基基础的安全系数，并且这种与有线差分法相结合的方法还具有节约计算时间的优点。该方法可以为以后的岩溶地区地基稳定性的类似工程提供参考。

［1］ 王华牢，张 鹏．隐伏岩溶洞群对公路隧道顶板承载力影响的研究［J］．公路交通科技，2010，27(2):91-96．

［2］ 赵明华，袁腾方．岩溶区桩端持力岩层安全厚度计算研究［J］．公路，2003(1):124-128．

［3］ 黎 斌，范秋雁．岩溶地区溶洞顶板稳定性分析［J］．岩石力学与工程学报，2002，21(4):532-536．

［4］ 李炳行，肖尚惠．岩溶地区嵌岩桩桩端岩体临空面稳定性初步探讨［J］．岩石力学与工程学报，2003，22(4):633-635．

［5］ 帅红岩，赵晋乾．贵州毕节机场岩溶发育特征及成因机理［J］．路基工程，2010(1):136-137．