幂级数应用于物理竞赛中的近似计算

石长盛

(南京外国语学校,江苏南京 210008)

物理模型通常是在实际问题的基础上,突出主要矛盾,忽略次要因素建立起来的.在物理竞赛中常常用到以下函数的幂级数展开式.

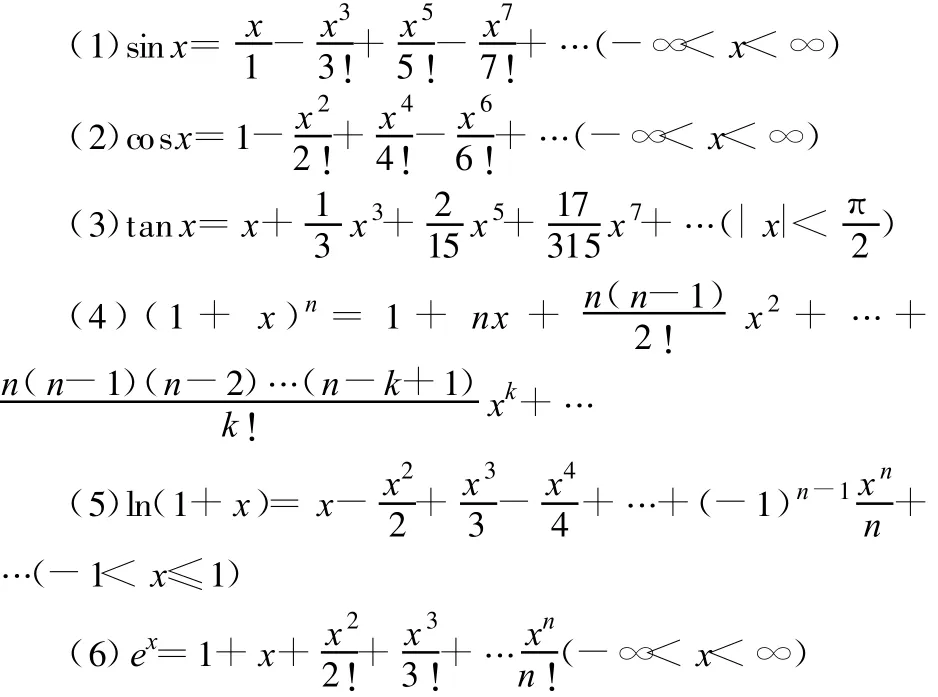
下面举例说明.

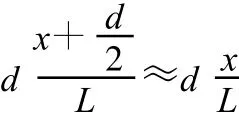
图1

例2.在 x轴的x=a和x=-a两位置上各有一个电荷量均为Q的固定电荷,在 x=0处有一电荷量为q、质量为m的自由小球,且 Q和q同号.今使小球沿着轴方向稍稍偏移δ释放,试证明小球将在 x轴上围绕O点做简谐振动.

解析:如图2所示,小球向右偏移 δ,则受合力指向 O点,大小为

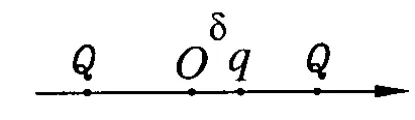
图2

即F合大小与位移成正比,方向与位移方向相反,故做简谐运动.

例3.一热气球的体积 V=1.2 m3,不可膨胀,气球外壳的质量为0.2 kg,其体积忽略不计.将气球内气体加热至110℃后,试问:

(1)气球可在离地多高处悬浮?

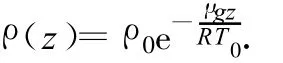
地面处大气密度为

热气球内、外压强相等,气球内空气密度为

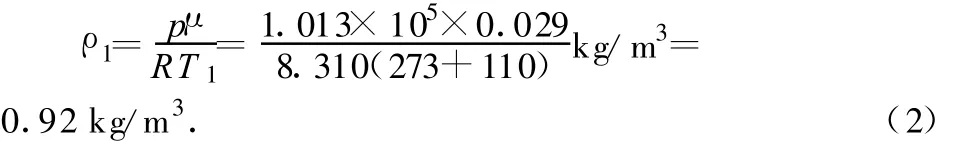
在h1高处气球外空气密度为

气球悬浮,气球总重力与浮力平衡,有

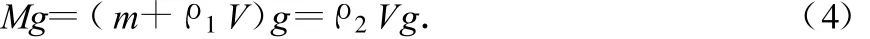
将(1)～(3)代入(4)式可得

(2)在 h平衡处,再升高 Δh,气球浮力减小,合力向下,大小为

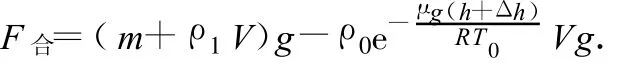
由于Δh≪h,利用幂级数展开式(6)有

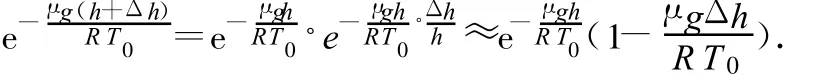
所以

由此式可看出,合力方向指向平衡位置,大小与Δh成正比.气球做简谐运动,角频率为

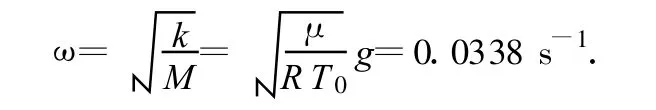
振动方程为