在学习功能关系时要关注的两个关系

朱庆松

(扬州市邗江区公道中学,江苏扬州 225119)

人类在认识能量的历史过程中,建立了功的概念,因而功和能是两个密切联系的物理量.利用功能关系是解决物理问题的重要途径之一.我们在学习功能关系时必须要理清两个关系.

1 力做功多少与所选参考系的关系

由功的定义可知,力对物体所做的功等于力的大小,位移的大小,力与位移夹角的余弦这三者的乘积.力与参考系的选取无关,但位移与参考系的选取有关,选取不同的参考系,位移不同,因而力对物体做的功就不一样.

例如,一物体在水平力F的作用下,沿力的方向在水平面上运动了一段位移s.如果选地面为参考系,F做的功为W=F◦s,若选物体为参考系,则 F做的功为 W=0,如图1所示.可见,一个力对物体是否做功,做功多少,取决于参考系的选取.为此,谈力做功时,也必须指明参考系.

图1

图2

对一对相互作用力而言,其中一个力对物体做功多少虽与参考系的选取有关,但这对力做功的总和却与参考系的选取无关.

例如,在光滑的水平桌面上,放一质量为 M的木板,一个质量为 m的木块,以速度 v0在木板上滑动,如图2所示.由于m、M间存在摩擦,当m在M上滑过s的距离时,M也在水平面上向前运动了L的距离.在此过程中,若以地面为参考系,则 M对m的摩擦力做功为W1=-f(s+L),m对M的摩擦力做功为W2=fL,总功 W=W1+W2=-fs;若以木板为参考系,则 M对m的摩擦力做功为W1′=-fs,m 对M 的摩擦力做功为 W2′=0,其总功 W′=W1′+W2′=-fs.与选地面为参考系的总功相同.

正是由于一对相互作用力做功的总和与参考系的选取无关,才为我们求解功能关系问题提供了方便.例如我们要研究一个系统的功能关系,如果系统内物体间无相对运动发生,那么无论系统内物体是否存在作用力(如弹力、静摩擦力等),它们所做功的总和均为零,因而不用去考虑它们的做功情况;如果系统内物体间有相对运动发生,那么,系统内物体间的作用力所做功的总和不为零,但无论选什么物体为参考系,功的总和均等于作用力与两物体的相对位移之乘积(注意:对于非保守力,如一对滑动摩擦力,这个功应为力与相对路程的乘积).

例1.如图3所示,质量为M的水平木板静止在光滑的水平地面上,板的左端放一质量为 m的铁块,现给铁块一水平向右的速度 v0,让铁块开始运动,并与固定在木板另一端的轻弹簧相碰后返回,恰好又停在木板左端,求:

(1)整个过程中系统克服摩擦力做的功?

(2)若铁块与木板间的动摩擦因数为μ,则铁块对木板的相对位移的最大值是多少?

(3)系统的最大弹性势能是多少?

图3

解析:(1)系统在水平方向不受外力,因而动量守恒,由此可求得铁块滑到左端时系统的总动能.由动能定理可求得系统克服摩擦力做的功为

(2)由于整个运动过程摩擦力大小不变,因而铁块相对于木板位移最大时,克服摩擦力做的功,应为全程 Wf克的一半.设最大位移为 s,则

所以

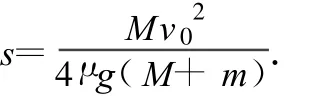
(3)弹簧压缩到最短时,木板、铁块的相对速度为零,此时弹簧压缩的距离最大,弹性势能也最大.系统的动能等于滑到左端时系统的动能,由能量守恒关系得,弹簧的最大势能为

2 做功与能量转化的关系

做功的过程就是能量的转化过程,做了多少功就有多少能量发生了转化.功是能量转化的量度,学习中要明确,究竟是哪一个力对物体做了功,相应地物体的什么形式的能发生了转化,转化成了什么形式的能.

在高一阶段,物理学中主要的功能关系有下列几种:

(1)重力(或弹力)对物体做的功,等于重力势能(或弹性势能)增量的负值,即 W重=-ΔEp(或 W弹=-ΔEp).重力(或弹力)做正功,对应重力势能(或弹性势能)转化为其他形式的能;重力(或弹力)做负功,对应其他形式的能转化为重力势能(或弹性势能).

(2)合外力对物体所做的功,等于物体动能的增量,即W合=ΔEk(动能定理).合外力对物体做正功,对应其他形式的能转化为物体的动能;合外力对物体做负功(或说物体克服合外力做功),对应物体的动能转化为其他形式的能.

(3)除重力(或弹力)外,其他力对物体所做的功,等于物体机械能的增量,即 W其他=ΔE机(功能原理).其他力对物体做正功,对应其他形式的能转化为机械能;其他力做负功,对应机械能转化为其他形式的能.

(4)只有重力(或弹力)做功,而其他力做功之和为零,则物体的机械能不变,即ΔE机=0(机械能守恒),对应物体动能和重力势能(或弹性势能)的相互转化.

(5)对相互作用力的做功情况:

①如果总和为零,说明相互作用的物体间无相对运动发生.这对力做功的结果,只是使机械能从一个物体转移到另一个物体上,但系统的机械能不变,并没有由于这对力做功而使系统的机械能与其他形式的能发生转化.

②如果这对力做功的总和为正值,说明相互作用的两物体间有相对运动发生.这对力做功的结果,除使一部分机械能从一个物体转移到另一个物体上外,还有其他形式的能转化为机械能(如炮弹炸裂、重核裂变等).

③如果这对力做功的总和为负值,说明相互作用的物体间也有相对运动发生.这对力做功的结果,除使一部分机械能从一个物体转移到另一个物体上外,还有机械能转化为其他形式的能.如一对滑动摩擦力做功,其总功为负值,大小为 W=-fs相对,做功的结果除使机械能在两物体间转移外,还有一部分转化为内能(摩擦生热).

例2.如图4所示,传送带与水平地面间的倾角为θ=37°,从 A端到B端长度为s=16 m,传送带在电机带动下始终以 v=10 m/s的速度逆时针运动,在传送带上 A端由静止释放一个质量为m=0.5 kg的可视为质点的小物体,它与传送带之间的动摩擦因数为μ=0.5,假设最大静摩擦力与滑动摩擦力大小相同,g取10 m/s2,求:

(1)小物体从A到B所用的时间.

(2)在这段时间内不计轮轴处的摩擦,电动机消耗的能量是多少.

图4

当速度达到10 m/s时,因物体受到的最大静摩擦力f静max=μ mgcosθ＜ mgsinθ,故物体继 续向下加 速,则mgsinθ-f′=ma2,f′=μ mgcosθ,所以 a2=2 m/s2.

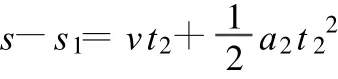
所以,小物体从A到B所用的时间为t=t1+t2=2 s.

(2)根据能量守恒,电动机消耗的能量和物体减少的重力势能转化成内能和物体的动能,有