基于Bootstrap的信用风险度量

段德峰，王建华，宋鸿芳

(武汉理工大学理学院，湖北武汉430070)

KMV模型是由KMV公司开发的一种违约预测模型。KMV模型将股权视为企业资产的看涨期权。以股票的市场数据为基础，利用默顿的期权定价理论［1－2］，估计企业资产的当前市值和波动率，再根据公司的负债计算出公司的违约点(即企业1年以下短期债务的价值加上未清偿长期债务账面价值的一半)，然后计算借款人的违约距离(即企业距离违约点的标准差数)，最后根据企业的违约距离与预期违约率(EDF)之间的对应关系，求出企业的预期违约率。模型具有理论基础扎实、动态性、前瞻性和准确性等优点，但同时有一些局限性。如模型假定资产收益正态分布的假设，使模型适用范围受到了限制。KMV模型特别适用于对上市公司的信用风险评估［3－4］;模型不能够对债务的不同类型进行区分等;在实际中，这造成了很大的误差。

1 KMV模型设定与参数估计

(1)假设资产收益的概率分布不随时间变化，对于公司股票的市场价值和股价的波动性及负债的账面价值，应用默顿的违约证券估价方法估计公司资产价值V及其波动性σv，计算公式为［5－6］:

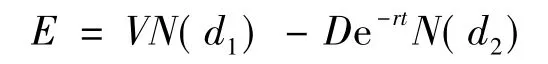
公司股票波动率与资产波动率之间的关系为:

(2)利用资产预期收益和系统风险的关系，根据资产回报的历史数据确定出资产预期收益，再结合资产的现值可得到资产的未来预期值。然后根据负债计算出公司的违约触发点DPT及违约距离DD，则DPT=企业短期债务价值+0.5×企业长期债务价值;

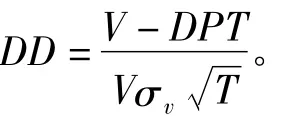
(3)计算预期违约概率(EDF)。

KMV模型参数估计值如表1所示。

2 实证分析

2.1 运用Matlab 7.04编程计算违约距离

根据计算得出的结果，对两组数据进行独立样本检验，假设:

表1 KMV模型参数估计值

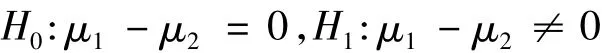
表1中前3个为样本x，后3个为样本y。由于数据属于小样本(n=3)，且总体方差未知，按照常见的做法接下来是构造统计量:

2.2 行业差异对KMV模型影响的实证研究

2.2.1 样本的选择

笔者以中国证监会2003年8月2日公布的《上市公司行业分类指引》为标准，选取房地产业和电力煤气及水的生产供应业两个具有典型差别和代表性的行业来进行研究比较。为保证计算结果的准确性和可比性，在两个行业中分别剔除ST类财务已经出现异常的公司和发行B股的公司，然后在所得到的样本中选取已经连续在本行业稳定经营两年以上的股票，最后得到的房地产行业样本数为29个，电力、煤气及水的生产与供应行业的样本数为47个。为了使两个行业比较更精确，笔者从电力、煤气及水的生产与供应行业的样本中按资产规模的大中小，选出29家公司为样本与房地产行业进行比较。所有样本采用2005年的数据，数据来源于国泰君安股票交易数据库系统和大智慧股票行情分析系统。

2.2.2 两个行业违约距离的计算

按上述违约距离的计算方法进行计算，其计算结果如表2所示。

2.2.3 基于Bootstrap的违约距离的总体均值分析

由于该模型在小样本情况下的计算结果不是很准确，且又不知道小样本的真实分布，故在此运用Bootstrap的方法［7－11］来确定样本的经验分布再进行计算。简单地说Bootstrap法就是对来自于总体分布规律未知的原始小样本的观测数据进行重复多次的有放回的再抽样，得到大量的新的Bootstrap样本及相应的Bootstrap统计量，用大量的Bootstrap样本来估计总体的分布规律，从而完成统计推断。故在此选取2个小样本，一个为房地产行业样本Y(29家)，另一个为电力、煤气及水的生产与供应行业样本X(29家)。再利用Bootstrap法分别计算出2个样本的F值和t值。

表2 两个行业样本的违约距离

总体均值分析的结果如表3所示，F值的概率为0.000 2，在显著性水平为0.05的情况下，F值落在拒绝域内。同时，组间方差均值大于组内方差均值，说明行业差别带来的违约距离的变化大于行业内各不同公司的违约距离。由此可见，两个行业的违约距离是有显著差异的。

上述实证结果证明了行业间违约距离差异的显著性，也即电力、煤气及水的生产与供应业的违约风险小于房地产行业。

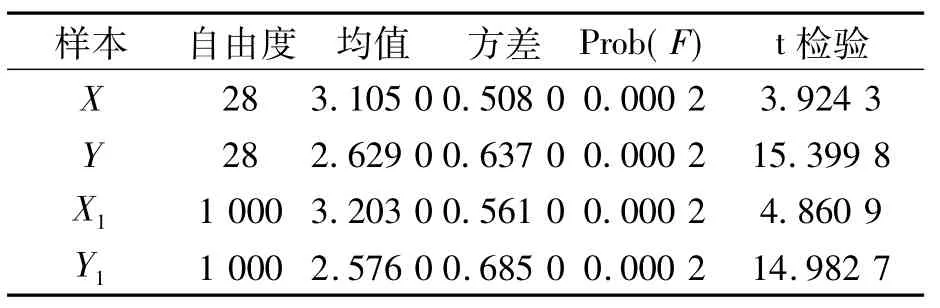
表3 总体均值分析的结果

3 结论

笔者运用基于Bootstrap的KMV模型，在信用市场中可获得有效数据较少的情况下，能有效和精确地按行业来评估违约风险，从而能完善信用市场风险管理。接下来可以对所选的样本进行进一步筛选，如可以对所选的样本中同一行业的公司按照业绩的优良中继续分成3个独立的小样本来计算，以进一步提高计算结果的准确性。

［1］王建华，董志华.奇点分离法在美式期权定价中的应用［J］.武汉理工大学学报:信息与工程工程版，2010，32(5):803－806.

［2］彭勇杰.基于高阶统计量的期权定价模型研究［D］.武汉:武汉理工大学图书馆，2009.

［3］王仁祥，喻平.金融风险管理［M］.武汉:武汉理工大学出版社，2004:41－86.

［4］JOSEPH S，VICTOR G.金融数学(英文版)［M］.北京:机械工业出版社，2004:28－133.

［5］飞利浦·乔瑞.金融风险管理手册［M］.张陶伟，译.北京:中国人民大学出版社，2004:441－445.

［6］飞利普·乔瑞.风险价值VAR［M］.张海鱼，译.北京:中信出版社，2005:322－368.

［7］EFRON B.More efficient bootstrap computations［M］.NewYork:Am statist Ass，1989:88－132.

［8］BERAN R.Estimated sampling distributions［J］.An Statist，1982(10):212－225.

［9］EFRON B，TIBSHIRANIR.An introduction to bootstrap［M］.NewYork:Chap man＆HallLtd，1993:12－35.

［10］EFRON B.Bootstrap methods:another look at the jackknife［J］.Ann Statist，1979(7):1－36.

［11］王建华，续云峰.不完全信息条件下信用风险建模与数值模拟［DB/OL］.［2010－11－07］.中国期刊网.