随机三角级数收敛性与Paley－Zygmund定理的推广

朱志锋，余 澜，黄 臻

(1.孝感学院 数学与统计学院，湖北 孝感432000;2.湖北大学 物电学院，湖北武汉430062;3.武汉铁路职业技术学院教务处，湖北武汉430205)

1 预备知识

不等式1如果正项随机变量X∈L1(Ω)，且a＞1，则:

不等式2如果正项随机变量X∈L2(Ω)，且0＜λ＜1，则:

引理2［3］设

2 主要结果

定理1［4］设{Xn}是独立随机变量序列，且

推论1设{Xn}是独立随机变量序列，，且，若，则若，则这就是Paley－Zygmund定理。

推论2设{Xn}是独立正随机变量序列，，且，则若

推论3设{Xn}是正项同分布随机变量序列，且，则:

证明Xn是同分布的，若E(Xn)=0，则Xn=0 a.s.，从而E(Xqn)=0与0＜E(Xqn)＜+∞矛盾。因此，0＜E(Xn)＜+∞，记0＜E(Xn)=M(M＞0)，当an≠0时(an=0此项anXn去掉)，E(anXqn)·

E－q(anXn)=E(Xqn)E－q(Xn)＜+∞［8］。由推论2可知:

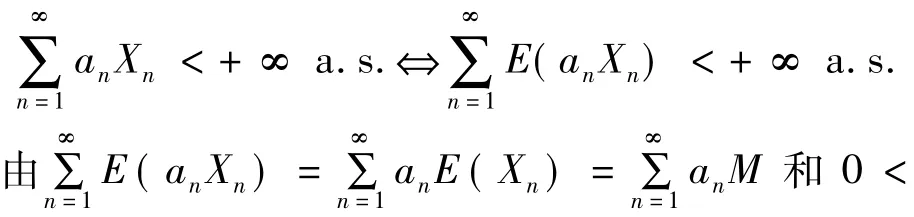
推论4设{Xn}是正项同分布随机变量序列，且0＜E(Xqn)＜+∞，q＞1，则:

由推论3和推论4易得:

推论5设{Xn}是同分布随机变量序列，且，则［9］:

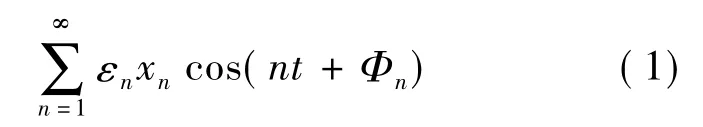
其中:xn和 Φn为给定的实数;{εn}为Rademacher序列。

显然式(1)是Rademacher级数［10］。

引理3{xn}和{Φn}是两个实数序列，则对几乎每个

引理5［11］，则式(1)几乎处处收敛。

当q=2时，可得以下特殊情形:

［1］张宏志.随机级数的收敛性［J］.数学杂志，1999(19):408－410.

［2］J·P·卡昂.函数项随机级数［M］.武汉:武汉大学出版社，1993:14－19.

［3］孟凡友.关于Fourier级数收敛定理的研究［J］.丹江师范学院学报:自然科学版，2000(1):102－104.

［4］章逸平，范爱华.Local inequalities for sidon sums and their applications［J］.数学物理学报，2005(2B):305－306.

［5］严家安.测度论讲义［M］.北京:科学出版社，2000:97－98.

［6］孙道椿，余家贵.一般容量的随机Taylor级数［J］.中国科学(A)，1996(26):884－891.

［7］吴桂荣.随机Taylor级数［J］.数学物理学报，1998(18):116－120.

［8］孙道椿.一个值分布定理在随机级数上的应用［J］.数学季刊，1990(5):1－5.

［9］陈建功.三角级数论(上)［M］.上海:上海科学技术出版社，1979:23－52.

［10］陈建功.三角级数论(下)［M］.上海:上海科学技术出版社，1979:136－138.

［11］ZYGMUND A.三角级数(英文版)［M］.3版.北京:机械工业出版社，2004:50－72.