图像去噪的改进自适应全变差正则化模型

郭晓龙，吴传生，刘 文，李云廷

(武汉理工大学理学院，湖北武汉430070)

图像去噪是图像处理领域中一个重要的分支，它是图像分割、特征提取与目标识别等图像处理过程的前提。由于传统方法在去除图像噪声的同时不可避免地破坏了图像的纹理信息，在不同程度上破坏了图像的完整性，影响了图像处理的下一步工作。如何在抑制噪声的同时能够很好地保留图像的纹理特征，是构建有效的去噪模型的至关重要的问题。

RUDIN等在1992年提出的全变差正则化模型(total variation，TV)是迄今最为成功的图像复原模型之一，在图像去噪领域得到了广泛的研究与应用。但该模型易将噪声当成图像边缘保留，使其在平滑区产生阶梯效应［1］。虽然基于L2范数的调和模型能有效地去除噪声，但图像的边缘易模糊［2］。SONG等在TV模型与调和模型的基础上提出了Lp(1≤p≤2)范数空间下的广义TV模型，但系数p的客观选取严重影响了该模型的图像去噪效果［3－4］。根据TV模型与调和模型的去噪特点，笔者为兼顾图像的平滑去噪与边缘保留，提出了图像去噪的自适应全变差正则化模型(adaptive total variation，ATV)，并采用8邻点数据［5］计算图像的梯度模值以自适应控制ATV模型的图像去噪过程，并对其梯度下降流方程进行了改进，提高了ATV模型在图像去噪中的稳定性。

1 自适应全变差正则化模型

令u为清晰的原始信号，f为含噪的观测信号，则含噪图像的数学模型为:

其中，n为零均值的高斯白噪声，其方差为δ。

目前全变差正则化图像复原模型主要集中在对L1范数空间和L2范数空间上的讨论，基于L1范数空间的TV模型并不惩罚图像的不连续区域，并且能够有效地保护图像的边界，但其光滑性不足，并带有分片效应。基于L2范数空间上的调和模型对光滑区域处理的效果较好，可以较快平滑噪声，但易导致图像轮廓模糊，边界消失［6］。两者优劣参半，将两者结合可发挥各自优点，于是笔者基于L1范数空间和L2范数空间提出自适应全变差正则化图像复原模型(ATV)。

其中Ω为图像区域，且自适应参数g(u)定义为［7］:

式中，Gσ(σ＞0)为高斯滤波器。

用高斯滤波器对图像进行预处理，其目的是去除小部分噪声，以减少将噪声当作假边缘的可能性，在图像的边缘区域，g(u)→0，此时式(2)近似于TV模型，能较好地保留图像边缘;在图像的光滑区域，g(u)→1，此时式(2)近似于平滑性较好地调和模型，能有效地去除噪声;在图像的其他区域，式(2)根据‖▽Gσ×u‖12的大小自适应地控制参数g(u)，使得自适应全变差正则化模型(ATV)能同时兼顾图像的边缘保留与平滑去噪。

利用变分原理得到式(2)的Euler－Lagrange方程，即:

当采用显示方案求解式(4)对应的梯度下降流时，此时的迭代时间步长 Δt需满足这一苛刻条件，使得式(4)很难收敛至最优解［8］。于是为稳定求解式(4)并扩大其应用范围，笔者在MARQUINA改进TV模型［9］的基础上，对式(4)的左边乘以梯度模值‖▽u‖12，得到其对应的改进梯度下降流方程:

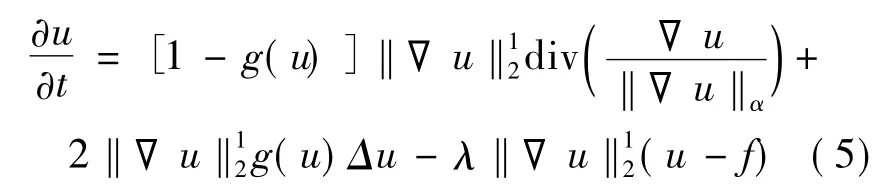
对于式(5)的求解，前两项采用中心差分做数值计算，而后一项将借助于迎风方案。

2 去噪模型的数值计算

计算式(5)时采用显式方案，即:

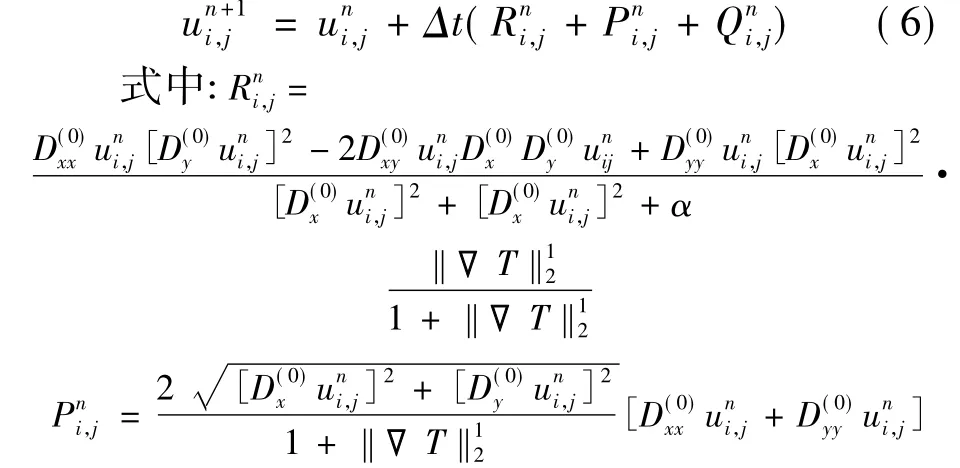
3 实验结果及分析

为验证改进自适应全变差正则化模型(ATV)在图像去噪中的有效性，笔者分别以Lady和Lena图像为实验对象，与MARQUINA提出的改进全变差正则化模型(MTV)的实验结果进行了比较分析，并采用峰值信噪比(PSNR)作为客观的评价标准，PSNR定义为:

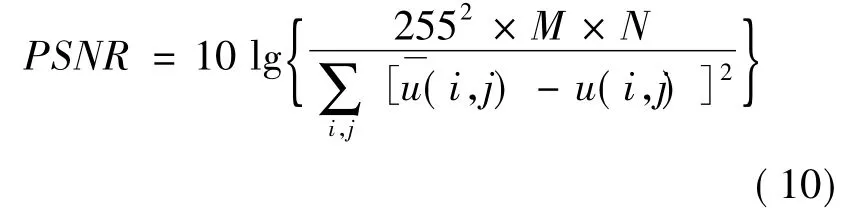
在该实验的仿真中，输入图像的大小均为256×256，灰度级为256，Lady和Lena图像中加性噪声的方差分别为0.005和0.010。其中高斯滤波器Gσ的窗口大小为3×3，时间迭代步长Δt=0.01，正则化参数 λ=0.2，实验结果如图1、图2和表1所示。

图1 降噪前后的Lady图(噪声方差δ=0.005)

图2 降噪前后的Lena图(噪声方差δ=0.010)

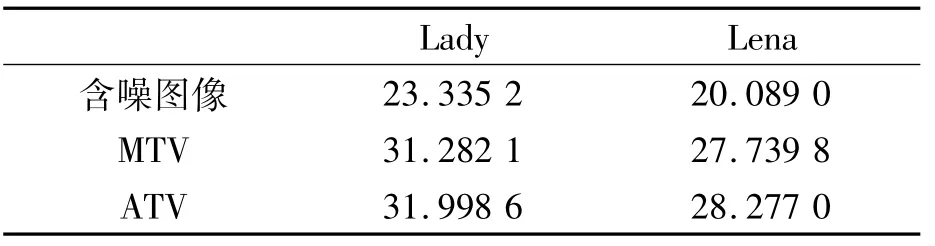
表1 各图像去噪方法的峰值信噪比dB

图1和图2分别为降噪处理前后Lady和Lena图像的视觉效果，从图中可看出MTV模型在去噪中能较好地保留图像的边缘信息，但同时易将噪声当作图像边缘进行处理，导致图像依然有部分噪声被保留。而笔者提出的正则化模型(ATV)能同时兼顾图像的平滑去噪与边缘保留，如表1所示，ATV模型较MTV模型在PSNR上有明显的提高，且人眼能直观地感受到复原图像质量的改善。

4 结论

笔者在分析TV模型(L1范数空间)与调和模型(L2范数空间)的基础上，构建了一种能同时兼顾图像平滑去噪与边缘保留的自适应全变差正则化模型(ATV)，并对其梯度下降流方程进行了改进，提高了ATV模型在图像去噪中的稳定性，有效缓解了传统TV模型中阶梯效应的问题。实验结果表明，笔者构建的自适应去噪模型在有效去除噪声的同时保留了图像的细节信息，得到的复原图像在峰值信噪比和主观视觉效果方面有明显提高。

［1］RUDIN L，OSHER S，FATEMIE.Nonlinear total variation based noise removal algorithms［J］.Physica D，1992，60(1/4):259－268.

［2］AUBERTG，KORNPROBST P.Mathematical problems in image processing:partial differential equations and the calculus of variations［M］.New York:Springer，2009:54－89.

［3］SONG B.Topical in variation PDE image segmentation，inpainting and denoising［D］.USA:University of California Los Angeles，2003.

［4］BLOMGREN P V.Color TV:total variation method for restoration of vector valued images［D］.Angeles:UCLA，1998.

［5］王大凯，侯榆青，彭进业.图像处理的偏微分方程方法［M］.北京:科学出版社，2008:140－148.

［6］张红英，彭启琮.全变分自适应图像去噪模型［J］.光电工程，2006，33(3):50－53.

［7］侯榆青，张欢，史晶，等.一种改进的全变分自适应图像去噪模型［J］.西北大学学报，2008(3):371－373.

［8］LEVEQUE R J.Numericalmethods for conservation laws［M］.Zurich:Birkhauser Verlah，1990:65－102.

［9］MARQUINA A，OSHER S.Explicit algorithm for a new time dependent model bassed on level set moton for nonlinear deblurring and noise removal［J］.SIAM JSci Comput，2000(22):387－405.

［10］李荣华.偏微分方程数值解法［M］.北京:高等教育出版社，2005:43－98.