基于BPNN－GA算法的双边多属性谈判求解

王高飞，邓立治，田金信，李 梅

(1.哈尔滨工业大学管理学院，黑龙江哈尔滨150001;2.黑龙江科技学院经济管理学院，黑龙江哈尔滨150027;3.北京科技大学经济管理学院，北京100083)

谈判是一个动态过程，在这个过程中，两个或多个具有不同标准、约束和偏好的参与者针对一个交易的相关条目共同达成一个可以相互接受的协定［1］。按谈判机制将谈判分为:一对一谈判(双边谈判)、一对多谈判和多对多谈判。其中，一对多谈判被看作是多个并发的双边谈判，多对多谈判可以通过一对多谈判扩展得到［2］。而多属性谈判更具实用性，因此笔者选定双边多属性谈判求解模型作为研究对象。目前，对于网上谈判模型求解的代表性研究方法有:博弈论模型［3］、以效用函数为基础的多属性决策模型［4－5］、对策分析法［6］、解决冲突的图形模型［7－8］和基于遗传算法的解支持方法［9－10］等。这些方法在一定程度上推动了谈判理论研究的进展，但仍没有完全解决多属性谈判中存在的以下问题:①多数算法采用线性函数，虽然简化了问题，但存在局部交易的退化和重要属性的作用被埋没等副作用［11］;②在非线性函数的复杂合同研究中，谈判存在着囚徒困境的问题;③在谈判求解过程中，忽略了属性之间的依赖关系［12］;④由于属性间复杂依赖关系与用户偏好获取的困难，使效用函数表达成为难题。

笔者针对上述问题，构建了BP神经网络与遗传算法的联合算法(BPNN－GA算法)，该算法充分利用遗传算法全局优化与BP神经网络非线性映射的优点，有效克服以上不足，求解谈判双方效用最大的谈判方案，实现双方的共赢。

1 双边多属性谈判决策模型

双边多属性谈判问题可以表述为:买方与卖方对双方关注的N项属性的各种可能方案进行谈判，直到达成一致或谈判失败。对于每种可能的方案，买卖双方都有一定的效用评价，谈判问题的目标就是寻求使双方效用最大的方案。该问题定义如下:

定义1 用i表示需要谈判的属性项，其中i=1，2，…，n。

定义2 用xij表示第i项属性的第j种可能取值，j=1，2，…，mi;xij∈Di，Di为第 i项属性的取值范围。谈判方案可用向量 X=［x1j，x2j，…，xnj］T表示。

定义3 在谈判中，谈判双方对当前方案的效用评价由各自事先训练收敛的BP神经网络进行。网络输入向量为 X=［x1j，x2j，…，xnj］T，网络输出值可作为双方对当前方案的各自效用评价值，可表示为Ub和Us。则对谈判问题的目标函数表述为:

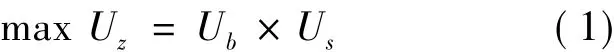
2 双边多属性谈判的BPNN－GA算法

2.1 BP神经网络

BP神经网络模型是神经网络中比较成熟、应用最广泛的一种神经网络模型。它是基于误差反向传播算法的多层前馈型神经网络。BP神经网络具备任意精度的函数逼近能力，具有自组织、自适应、自学习、高度非线性映射性、泛化性和容错性等优点。假定网络有m个隐含层，输入层X=(x1，x2，…)，输出层Y=(y1，y2，…)，第s层节点数为ns，ysk为s层节点k的输出，Wsk是上一层与第s层节点k的连接权重，如式(2)和式(3)所示。一般而言，神经元常用Sigmoid函数，如式(4)所示。

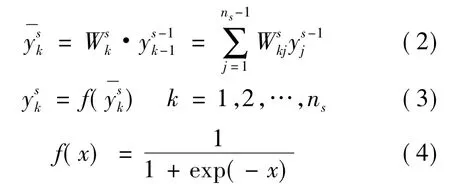
基于BP神经网络的上述特点，使之在具有非线性函数复杂合同谈判中的运用成为可能。神经网络输出是买方或卖方对某谈判方案的评价值，网络拓扑结构简化为如图1所示的3层网络的单维输出，其中U为输出的评价值。

2.2 遗传算法与BPNN－GA算法求解模型

遗传算法(genetic algorithm，GA)是模拟达尔文遗传选择和自然淘汰生物进化过程的计算模型。基于遗传算法进行优化求解，需要进行编码、确定初始群体、计算适应度、选择、交叉、变异以及终止等操作。遗传算法具有简单、鲁棒性强、全局最优性、可并行性及高效率等优点。由于它不受搜索空间限制性假设的约束，不要求诸如连续性、导数存在和单峰等假设，能够从离散的、多极值的、含有噪音的高维问题中以较大的概率找到全局最优解，因此在解决多属性谈判中具有广阔的应用前景。

传统的遗传算法的适应度函数必须是具有明确数学表达式的函数方程，但实际上，每个谈判者的偏好不同，方案中各属性间依赖关系较复杂，如何确定谈判各属性值与谈判者的满意度(效用)之间的显式(可以用数学方程明确表示)函数关系是非常困难的。笔者针对多属性谈判特点，将BP神经网络用于谈判提议方案的效用评价，以谈判双方效用评价值之积的目标函数作为遗传算法的适用度函数，形成求解此类谈判问题的BPNN－GA算法。将上述的思路转化成模型，如图2和图3所示。

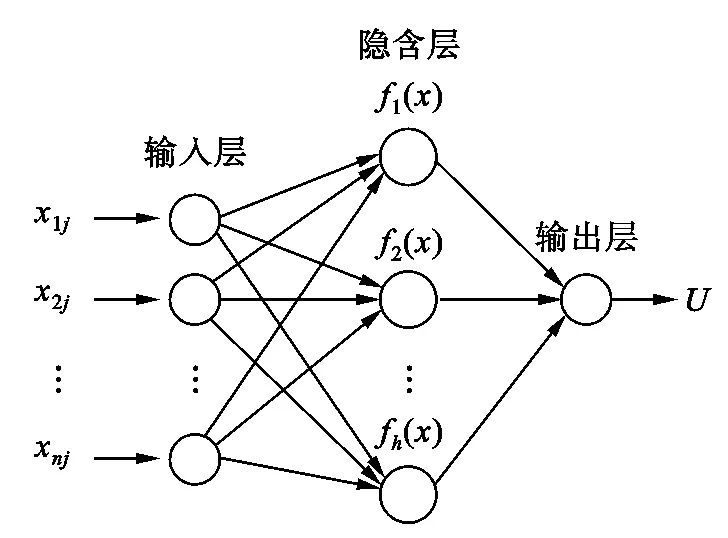
图1 BP神经网络结构图

图2 目标函数模型

图3 基于BP－GA算法的谈判问题求解流程

2.3 BPNN－GA算法求解过程

2.3.1 BP网络样本选取与数据处理

在谈判前双方就所要谈判的款项(属性)i具体类别与每项条款的取值范围Di达成一致，并据此准备BP网络的训练样本。由计算机在取值范围内随机生成多组数据并遵循适度均匀原则，由专家给出对应评价值。对于样本数据的处理，输入数据采用线性刻度转换方法进行归一化，如式(5)所示。x*为归一化后的样本数据，输出数据为百分制得分，训练时按分数/100进行归一化处理。

2.3.2 BP神经网络创建与训练

在使用Matlab工具箱创建BP网络时，采用newff函数设计3层BP网络，神经元的传输函数采用logsig函数，如式(4)所示，网络结构如图1所示。BP网络训练方法很多，笔者采用LM算法。LM算法是由高斯－牛顿法演变而来的，该算法极大提高了收敛的速度，弥补了标准BP算法收敛速度慢的不足，克服了牛顿法易振荡发散的缺点。

2.3.3 遗传算法的步骤

(1)编码与解码。针对谈判问题的实际情况，采用二进制编码的方法，但需考虑精度。对于给定区间［p，q］，设二进制编码长度为l，则任何一个变量可表示为:

对应二进制编码p1，p2，…，pl，二进制编码与实际变量的最大误差为(q－p)/2l。解码是编码的逆过程。由于定义2中谈判方案可用向量X=［x1j，x2j，…，xnj］T表示，则每个染色体对应一个谈判方案，染色体编码可以用n组二进制编码表示。

(2)确定适应度函数。适应度是评价群体中个体优劣的函数，其值越大，个体越有可能被选中进行交叉、变异操作，个体特性便越有可能遗传到下一代。由式(1)可直接转化为适应度函数如式(7)所示，显然是要求使适应度函数值最大的方案，如图2所示。

Ub是买方对谈判方案向量X输入买方BP神经网络NetB的输出评价值;Us是卖方对谈判方案向量X输入卖方BP神经网络NetS的输出评价值。具体映射关系见式(4)和图1。

(3)确定选择、交叉和变异算子。选择算子是遗传算法用来对群体中个体进行优胜劣汰的操作，并不生成新的个体，选择算子采用轮盘选择与最佳保留策略。交叉算子是指两个相互配对的染色体按某种方法相互交换其部分基因，从而形成两个新的个体。它在遗传算法中起着关键作用，是产生新个体的主要方法，它决定了遗传算法的全局搜索能力，这里采用离散重组交叉算子。为避免陷入局部最大值，变异算子采用离散变异算子。

(4)终止规则。由于适应度目标值无法事先确定，并且多次迭代容易影响计算时间。因此笔者采用设定未改善当前解的最大代数，如设未改善当前最优解100代后终止运算。

3 谈判实例

企业A与企业B就企业B销售的某种商品进行网上谈判。双方选定的谈判商品属性与取值范围为:商品的单价(4～5万元)，商品的质量(100%～90%优良率)以及商品交付时间(12～72 h);企业A与企业B的归一化后样本数据如表1所示。为简化算法说明，表1中输入数据由计算机系统随机生成并按式(5)进行归一化处理，当然在实际应用中可由各企业自行准备训练数据。输出数据为企业A与企业B的专家组针对系统生成的不同方案的百分制打分值，并除以100进行归一化。该处选择了35组训练样本和5组检验样本。如训练精度未达到要求则增加训练样本数量。经训练后，企业A的BP神经网络NetB训练结果如图4所示，企业B的NetS训练结果如图5所示。由检验样本得到的仿真结果与实际评价结果的平均误差分别为3.2%和2.8%，小于预期可接受误差5%，训练达到预定要求，可以用于谈判运算。BPNN－GA算法的适应度值与种群均值经128代进化后终止运算，结果如图6所示。最终计算结果如表2所示。

表1 归一化后的样本数据

图4 NetB训练过程

图5 NetS训练过程

图6 经过128次迭代后的优化解性能跟踪

表2 运算结果

从表2的运算结果可以看出，算法在28代达到最大值，迭代100代后无改善，程序终止。最终的谈判方案为:商品价格4.519 1万元，商品质量为92.752%的优良率，交货时间为50.676 h。企业A的满意度为50.57%，企业B的满意度为54.57%，谈判的目标函数最大值(适应度函数最大值)为0.276 0。

4 结论

针对原有线性效用函数假设的局限性，笔者提出了BPNN－GA双边多属性谈判求解算法，通过基于样本数据的BP神经网络训练，逼近具有复杂属性依赖关系的非线性效用函数映射，合理避免了对非线性效用函数方程的结构设计与参数求解难题。放松了原有方法的约束条件，为双边多属性谈判提供了更具一般性的求解方法，为该类问题研究提供了新的思路。同时，将双边优化模型进行适当拓展可以用于一对多谈判和多对多谈判，具有广阔的应用前景。当然，由于该问题的复杂性以及算法的初次引入，新算法还有较大的改进空间。例如，进一步提高BP神经网络逼近精度，合理选择样本数据，特别是为降低谈判双方的评价工作量，如何在小样本数据情况下实现较高精度求解等将是下一步研究的重点。

［1］JENNINGSN R，FARATIN P，LOMUSCIO A R，et al.Automated negotiation:prospectsmethods and challenges［J］.International Journal of Group Decision and Negotiation，2001，10(2):199－215.

［2］RAHWAN I，KOWALCZYK R，PHAM H H.Intelligent agents for automated one－to－many e－commerce negotiation［C］//Twenty－Fifth Australian Computer Science Conference.Melbourne:［s.n.］，2002:197－204.

［3］CHE Y K.Design competition throughmultidimensional auctions［J］.RAND Journal of Economics，1993，24(4):668－680.

［4］MARTIN B.An experimental analysis ofmulti－attribute auctions［J］.Decision Support Systems，2000，29(3):249－268.

［5］FARATIN P，SIERRA C，JENNINGSN R.Using similarity criteria to make negotiation trade－offs in automated negotiations［J］.Artificial Intelligence，2002，142(2):205－237.

［6］TEICH JE，WALLENIUSH，WALLENIUS J.Advances in negotiation science［J］.Transactions in Operational Research，1994(6):55－94.

［7］LIK W，HIPELKW，KILGOUR D M，et al.Preference uncertainty in the graph model for conflict resolution［J］.IEEE Transaction Systems，Man and Cybernetics，2004，34(4):507－520.

［8］孙华梅，李一军，曹荣增，等.基于约束放松的电子商务协同谈判模型［J］.运筹与管理，2008，17(4):132－137.

［9］李玥，冯玉强，王衍华，等.遗传算法在网上谈判支持系统中的应用研究［J］.系统工程理论与实践，2002(6):87－92.

［10］董婷婷，冯玉强.基于辩论的谈判解支持研究［J］.预测，2009(2):76－80.

［11］DE PAULA G E，RAMOS F S，RAMALHO G L.Bilateral negotiation model for agent－mediated electronic commerce［C］//AMEC 2000.Berlin:Springer，2001:1－14.

［12］FUJITA K，ITO T，KLEINM.Finding nash bargaining solutions for multi－issue negotiations:a preliminary result［C］//Proceedings of the 1st International Working Conference on Human Factors and Computational Models in Negotiation.New York:ACM，2009:63－70.