带参照链的供应链纵向竞合博弈的建模与求解

胡宪武，滕春贤

（1温州大学 城市学院，浙江 温州 325035；2哈尔滨理工大学 系统工程研究所，哈尔滨 158100）

0 引言

在博弈论中，完全信息是指对于所有博弈方（players）来说都能够了解到其他博弈方（players）在博弈对局中的一切信息。也就是说，市场中的竞争者彼此了解各自的竞争策略、并清楚各博弈方（players）在不同组合策略下的效用。完全信息是一个有效率的完全竞争市场所必需的理论前提条件。在某种意义上，它也是经济理论中“经济人(理性人)假设”所必需的条件。完全竞争也好，完全垄断也罢，其实都是经济学上的一种理论假设。如果说完全竞争强调的是市场机制是如何优化配置资源，那么完全垄断强调的是某种产品只有唯一市场供应者，但并不能完全排斥不同产品之间的竞争。介于完全竞争和完全垄断之间的寡头垄断是一种比较典型的市场类型。本文将讨论的是基于参照链的供应链链际竞合博弈分析这一主题就是以寡头垄断市场作为研究背景，以不同供应链企业间的产品具有完全的高度可替代性作为前提的。因为研究的目标主体是不同的两条或多条供应链，所以就存在链间横向同级企业间的同时决策与链内企业间纵向的先后决策问题。所以，本文将同时借助经典博弈论中的古诺(Cournot)产量竞争模型以及斯塔克博格(Stackelberg)产量竞争模型进行讨论分析。

1 问题描述

市场份额(Market shares)，即一个企业的销售量(或销售额)在市场同类产品中所占的比重。市场份额能直接反映企业所提供的商品和劳务对消费者和用户的满足程度，也能表明企业的商品在市场上所处的地位。市场份额越高，表明企业经营、竞争能力越强。因此，市场份额常常作为企业决策时的重要参量，我们研究讨论供应链企业间的竞合关系，也可以把这个参量引入模型中，用来判断供应链企业竞合策略下的竞争优势。

为研究方便，提出相应的研究假设与研究范围，并对模型中涉及到的符号与参量进行描述。

假定供应链企业所处市场结构为完全信息、寡占垄断。各节点企业是个体理性与集体理性兼备，并且集体理性服从个体理性的；每条单链中都是由一个制造商和一个零售商组成的二层供应链结构。制造商为核心企业，具有优先定价权；每条单链内是产销平衡的，即零售商的市场供应量等于向制造商的采购量，不存在缺货的情形；只考虑一个需求周期；市场零售价格满足线性关系P=a-bQ，a为产品的最高价格，b为产量对价格的影响因子，即产量对价格的边际负影响，a≥0,b≥0，同一市场下，各零售商的零售价格是相同的；在建模时，以某一单链作为研究对象，另一单链作为参照链，并以相对独立的博弈方（players）存在，一并构成一个完整系统。其参与竞争的可替代产品的成本为平均成本（设为某一常数）；各节点企业为风险中性；不考虑第三方物流与库存问题。

符号描述如下：

Mi：第i个制造商(i=1,…,n)；Ri：第i个零售商；P：市场零售价格；PMi：制造商Mi向零售商Ri售卖产品的转移价格；qRi：零售商i向制造商i提出的订购量，与零售商向市场提供的供给量相等，即产销平衡；CMi：制造商Mi的产品单位成本；CRi：零售商Ri用于产品销售的附加成本；：参照链的平均成本；πMi：制造商Mi的效用；πRi：零售商Ri的效用；πSi：第i条单链的总效用；βi：零售商i所在供应链Si所占市场份额；βi1：合作-合作模式最优条件下，供应链Si所占市场份额；βi2：竞争-竞争模式最优条件下，供应链Si所占市场份额；βi3：合作-竞争模式最优条件下，供应链Si所占市场份额；βi4：竞争-合作模式最优条件下，供应链Si所占市场份额；E：最优条件下，市场需求价格弹性。

按照假设条件，明确了制造商为核心企业并具有优先定价权，零售商与制造商的博弈关系为：首先制造商确定最优产品价格，接下来零售商则根据自己的总成本确定自己的订单，订单数量等于最优销售量。又由于供应链中的企业所处市场结构为完全信息的，各节点企业间的成本、策略集、效用函数等对上下游企业来说都是透明的。各节点企业对自己的产品数量及售价决策时，会优先考虑自己利益的最大化，同时又要兼顾合作伙伴企业的收益与决策。

制造商Mi的效用函数可以描述为

零售商Ri的效用函数可以描述为

第i条单链的总效用函数为

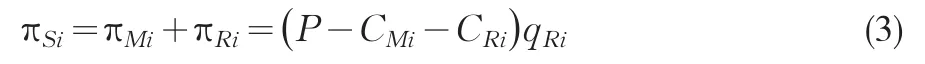
2 模型建立及求解

供应链中各节点企业的效用取决于不同的策略组合。策略选择又是由不同的理性意识支配的。在建模时，考虑不同策略组合下对企业收益及竞争地位带来的影响，进一步确定供应链竞合的最佳策略。

2.1 合作-合作博弈模型及求解

完全合作动态博弈模型描述的是供应链成员首先是集体理性的，即把供应链整体利益放在优先考虑的地位，也就是说制造商确定产品价格PMi，以及零售商确定订单量qRi的决策，都是以供应链的整体利益最大化为目标的，属于典型的集中控制下的供应链管理和运作模式。这样可以有效地克服“双重边际化”现象。

可以对第i条单链的总效用函数进行优化，由式(3)对销售量qRi求偏导并令导函数为零，即

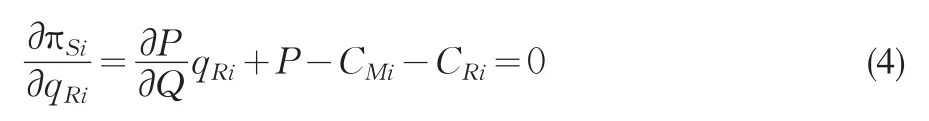
由式(4)整理得：

这里：

式(6)，(7)分别表示市场提供量在最优条件下的需求价格弹性和零售商的市场份额。

由式(6)整理可得：

由假设，产品的市场价格满足逆需求函数P=a-bQ，所以有分别代入式(7)得

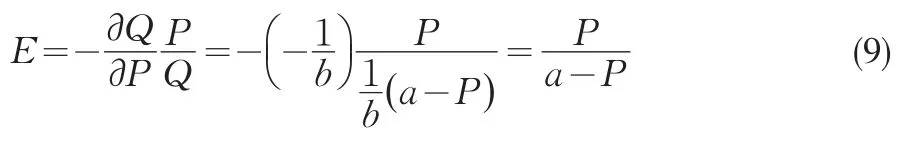
将式(9)代入式(7)，即可得到完全合作市场结构下各供应链终端零售商采取最优销售量时的均衡价格为

将式(10)代入逆需求函数P=a-bQ可以得到当前市场结构下市场均衡需求总量为

把式(9)代入式(11)整理可得零售商Ri的均衡订购量为

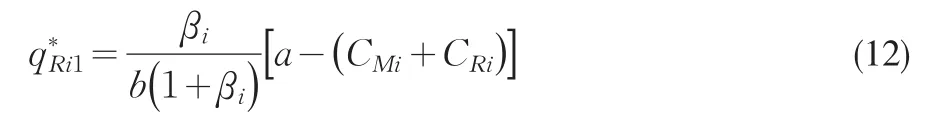
将式(10)、(12)代入式(3)即可得到合作-合作模式下供应链总效用为

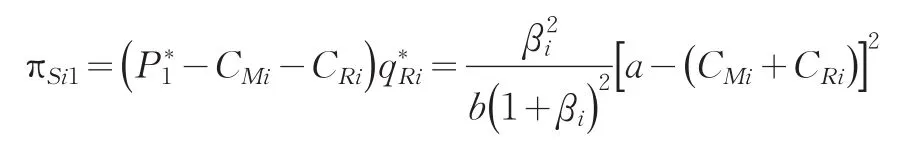
由经济学理论，寡头垄断市场上各同质产品价格趋于一致性原理，由式(10)可推导出参照链的市场均衡价格可描述为，且满足

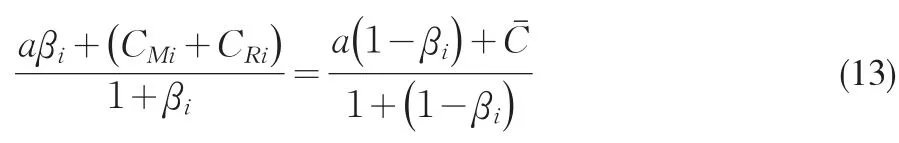
由式(13)可解得零售商Ri的均衡市场份额为

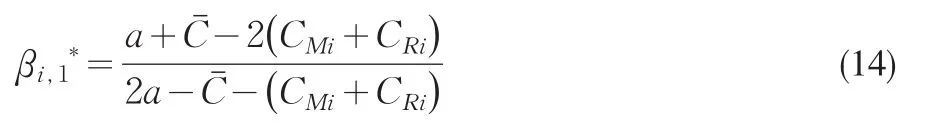
2.2 竞争-竞争博弈模型及求解

完全信息竞争博弈是指供应链各节点企业间个体理性占主导，制造商和零售商都各自以最大化自身利益为目标。这种供应链管理和运作方式属于分散控制方式。由于各供应链成员考虑的是局部最优，容易产生“双重边际化”效应。博弈过程为：先由制造商Mi给出向零售商售卖产品的转移价格PMi，零售商Ri则根据制造商提供的产品转移价格PMi来选择自己的最优订购量qRi。

此时的博弈属于Stackelberg博弈。博弈过程分为两个阶段，可以采用逆向归纳法求解。第二阶段，首先求解零售商所选择的最优订购量qRi。由式(2)对订购量qRi求偏导，并令导函数为零则有

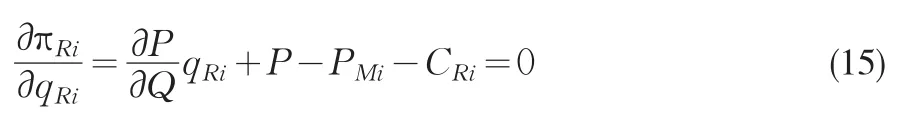
与式(15)同理可以求得

βi2为完全竞争情形下的零售商Ri的市场份额，产量最优条件已经不同于完全合作情形。在完全合作模式下零售商销售成本为CMi+CRi已经变更为完全竞争模式下的PMi+CRi。处于同一市场结构下的参照供应链平均成本Cˉ保持不变。

由经济学市场结构理论，均衡市场份额由市场上各企业的成本结构关系决定的。市场份额与企业成本成反比例变化的，即成本越高，市场份额越低；反之，成本越低，市场份额就越高。

把式(16)代入逆需求函数，可得产品在市场上的最优销售量为

将式(18)代入式(2)即可得到零售商Ri在市场结构下的均衡利润为

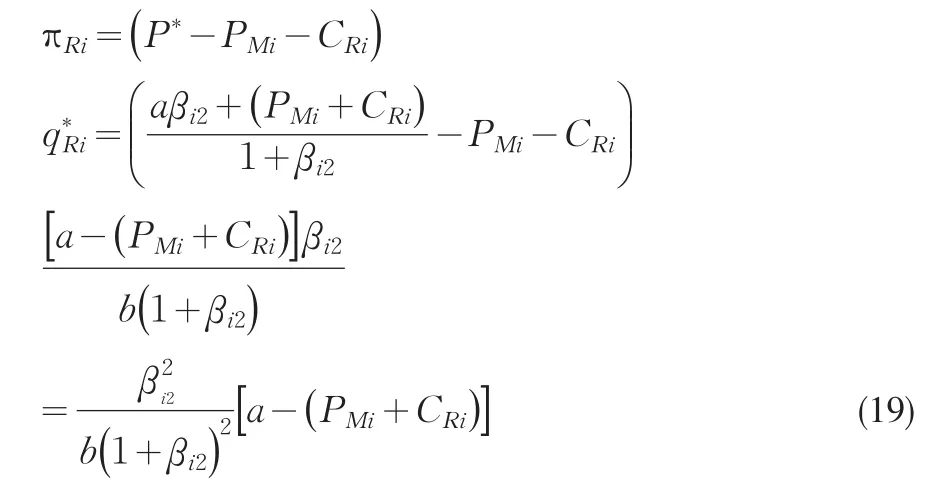
将式(18)代入式(1)即可得到制造商Mi的均衡利润为

与式(15)同理可以得到该市场结构下处于供应链终端的零售商Ri的市场份额为

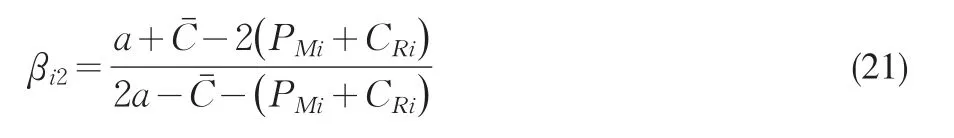
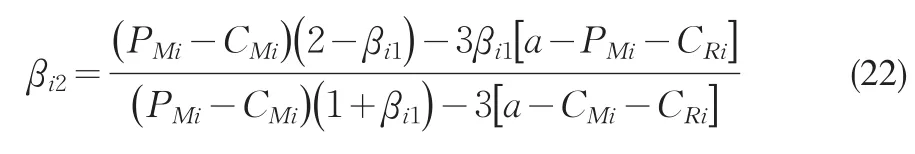
进入第一个阶段，制造商确定均衡转移价格P*Mi。把式(22)代入式(20)可以得到制造商关于转移价格的效用函数

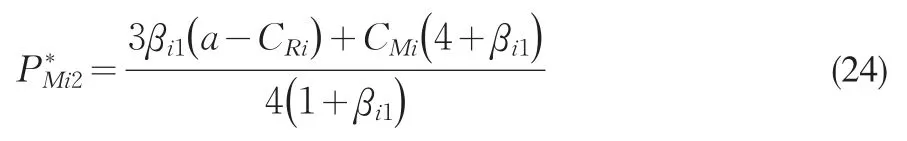
把式(22)和式(24)代入式(1)、(17)可得制造商Mi的均衡利润以及需求市场的均衡总产量为

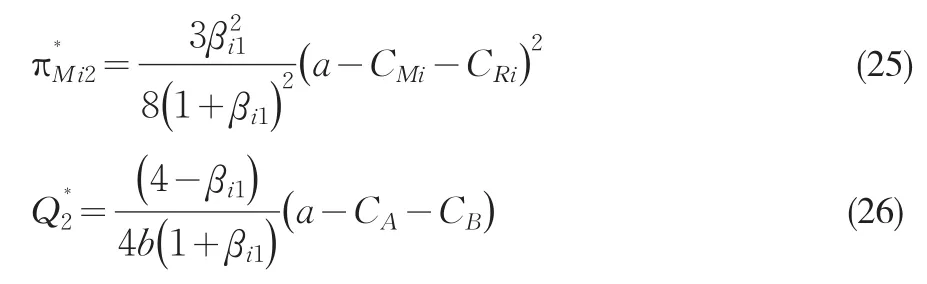
同理可以进一步求得销售商Ri的均衡产量

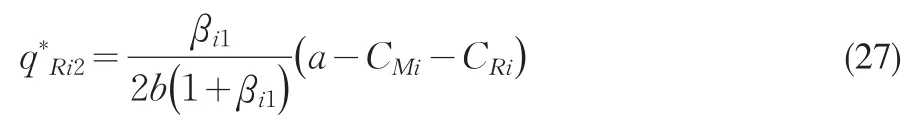
均衡市场占有率

均衡价格

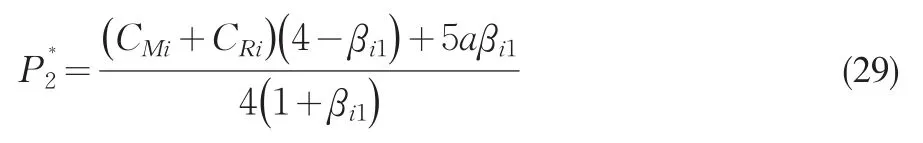
均衡利润

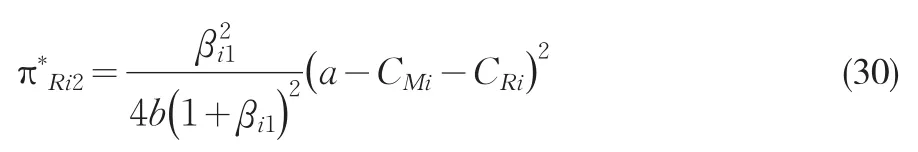
在完全竞争模式下供应链总效用为

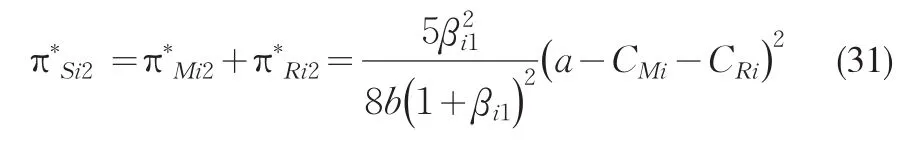
2.3 合作-竞争博弈模型及求解

竞合动态博弈模型的建立基础是制造商和零售商至少有一家在决策时首先是集体理性的，即为了链内集体合作的最大收益而暂时放弃自身利益最大化原则，其余合作伙伴在与横向参照链同层企业进行竞争时，甚至可以暂时不考虑合作伙伴的利益，只追求自身利益的最大化。首先考虑合作-竞争博弈。具体博弈过程如下：制造商Mi在确定产品的转移价格PMi时，首先考虑的是最大化自身和零售商的总体利益，即maxπSi；零售商再依照产品转移价格PMi来确定自己的最优订购量qRi，零售商的决策是以最大化自身利益为目标的。

本模型亦属于Stackelberg博弈。博弈过程的讨论可以分为两个阶段。第二个阶段与完全竞争模型一致。所以，零售商的最优决策及决策结果可以参照完全竞争的情形。

最优市场零售价

最优订购量

市场占有率

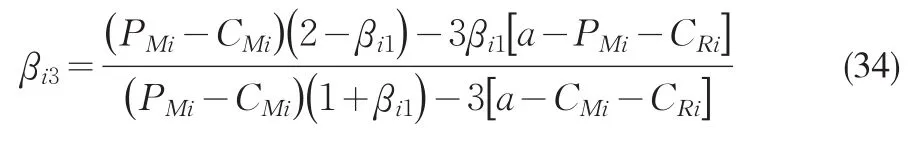
零售商效用

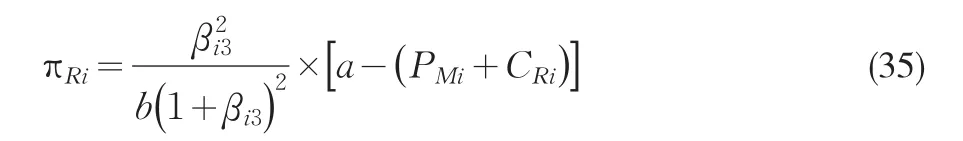
制造商效用

供应链总体效用

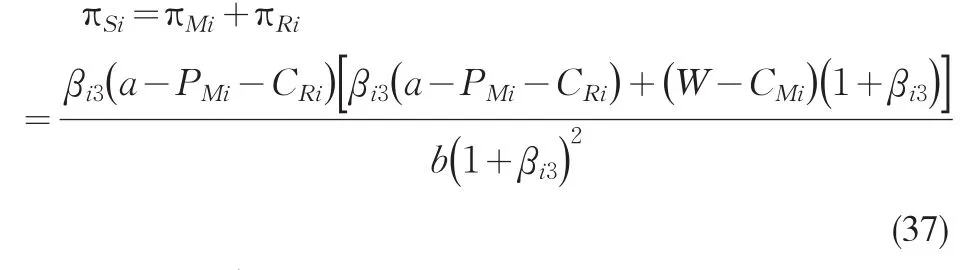
把式(34)代入式(37)进一步整理得

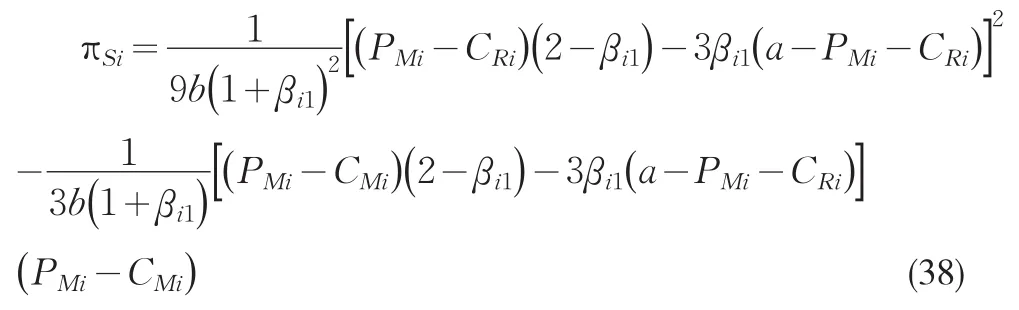
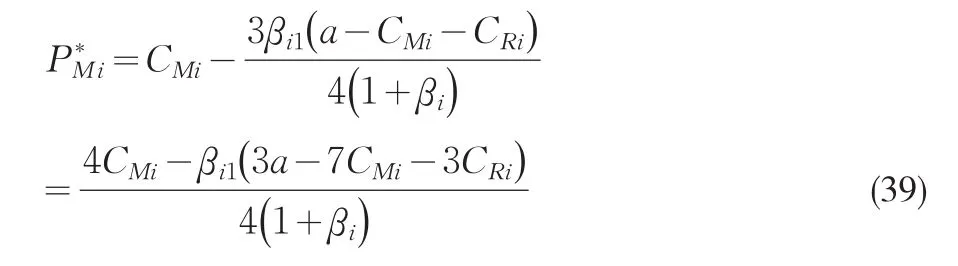
在合作-竞争动态博弈模型下制造商与零售商均衡决策及相应的均衡结果如下，把代入式(34)可求得零售商Ri的均衡市场份额为

制造商Mi的均衡利润

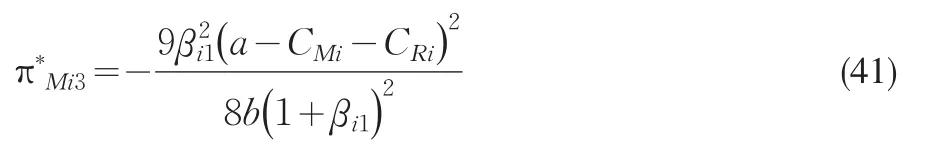
市场供给的均衡产品总量

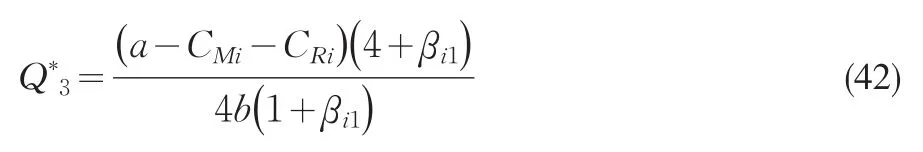
零售商Ri的均衡订购量

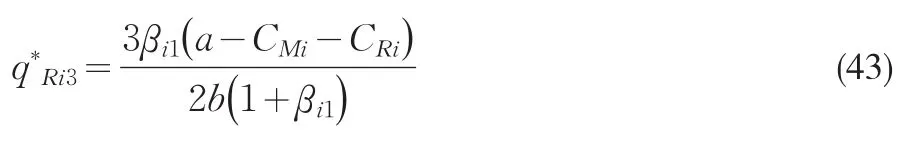
零售商Ri的均衡利润

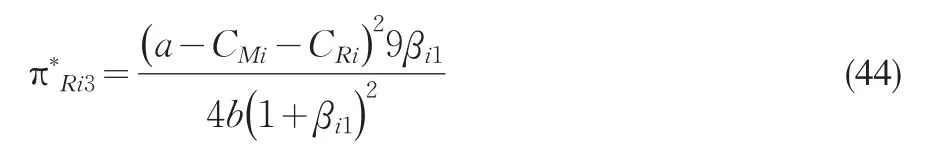
均衡市场零售价格

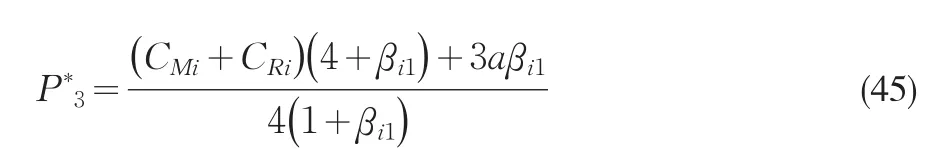
合作-竞争博弈模式下，供应链总利润

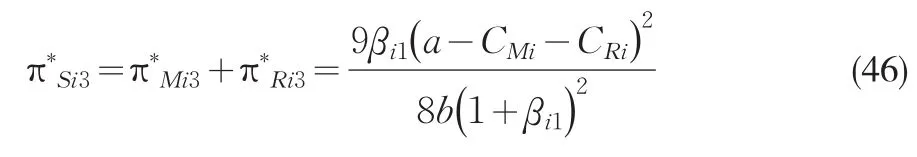
2.4 竞争-合作博弈模型及求解

完全信息下，竞争-合作博弈模型描述的是二层供应链节点企业中制造商Mi首先在选择转移价格PMi时以最大化自身效用为目标，而零售商Ri在选择订货量qRi时，是以最大化供应链整体效用为目标的。

求解依然采用逆推归纳法。在第二阶段，零售商Ri以最大化供应链整体效用对订购量qRi进行决策。

由式(3)知道 πSi=πMi+πRi=(P-CMi-CRiqRi)，结合式(11)、(13)、(15)即可得到零售商Ri最优零售价、最优订购数量以及最优市场份额，即

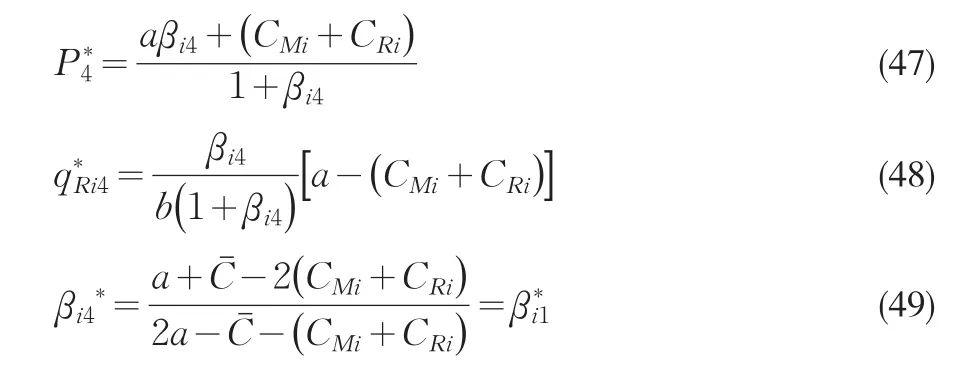
可以将式(48)、(49)代入式1得

第一阶段，制造商Mi确定转移价格PMi是以最大化其自身效用πMi为目的。可以对式(50)求偏导，并令偏导数为零。即可以求出制造商Mi的均衡价格

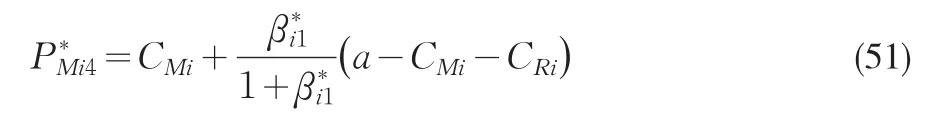
进一步可以求出

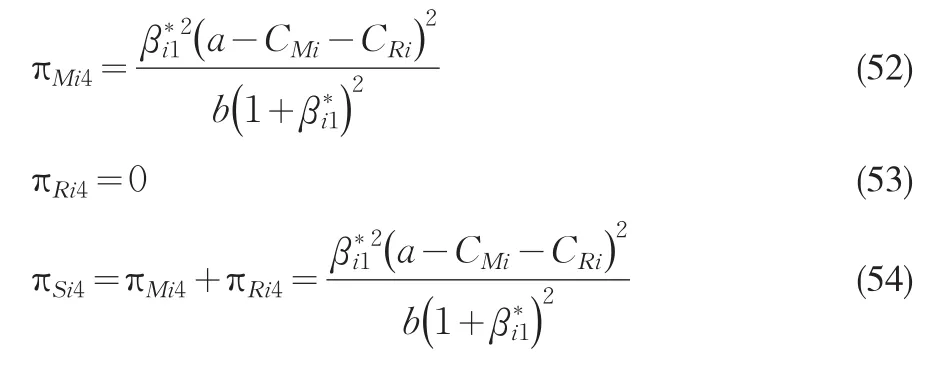
2.5 四种模型的比较与分析

从制造商与零售商的均衡决策变量与均衡结果两方面进行比较，可以得到以下结果：

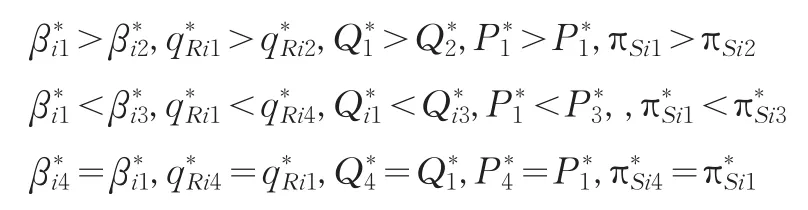
结果表明，在完全合作模式下的供应链整体绩效与完全竞争模式相比是高效率的。这是因为前者作为供应链节点企业的制造商和零售商都是以供应链整体绩效最大化作为目标的。而完全竞争模式下供应链节点企业都是以自身效用最大化为目标的，容易产生“双重边际化”效应。所以，完全信息下的完全合作模式可以实现供应链各节点企业的集中决策，以便提高零售商的市场份额，进而提升供应链总体效用。对于第四种的竞争-合作模式的均衡效果与合作-合作模式等价。原因是假设以制造商为核心企业，符合供应链集中管理模式下整体运作规律。第三种合作-竞争博弈模式与完全合作模式相比，供应链绩效又有了提升。在完全合作模式下，制造商可以做到零利润以增强供应链的竞争力，把市场联合做强。合作-竞争模式下制造商甚至可以不惜牺牲利润为代价，即来支持零售商参与市场竞争，零售商有了成本优势即可进一步扩大市场份额。同时，供应链整体绩效得到进一步优化。但此时对于同一市场结构下横向竞争的参照链对于这种情景会做出相应的反应，自身同样会改变供应链结构、降低平均成本，加大市场投放量，降低售价等方式，甚至会通过相关法律控告对方供应链企业低价倾销以抵抗不正当竞争行为，使得供应链链际竞合会走向一个新的竞争结构形态。但就目前市场结构条件下，对于合作-合作、竞争-竞争、合作-竞争、竞争-合作四种模式的结果分析，在确保集体效用较高的同时，还要考虑如何平衡供应链内各节点企业间的利益分配，这是供应链长期稳定合作的基础。所以，接下来讨论的关键问题是合作-合作模式下，收益在零售商与制造商之间如何分配，竞争-合作、合作-竞争模式下是否能实现吗。如果能实现，其途径与保证机制是什么。

3 结论

供应链企业间的竞争与合作关系不仅受到链内因素的影响，还要受到竞争链(参照链)的影响。本文选取了二层供应链，在与参照链同一市场结构下存在竞争时的制造商与零售商间的四种竞合形态，即合作-合作、竞争-竞争、合作-竞争、竞争-合作。分别对四种模式进行了建模与求解。

[1] Luoy A.Coopetition Perspective of Global Competition[J].Journal of World Business,2007,42(1).

[2] Mchirgui Z.The Economies of the Smart Card Industry:towards Competitive Strategies[J].Econ.Innov.New Techn,2005,14(6).

[3] Das T K,Teng B.Instabilities of Strategic Alliances:An Internal Tensions Perspective[J].Organization Science,2000,11(1).

[4] Gnyawali D R,Madhavan R.Cooperative Networks and Competitive Dynamics:A Structural Embeddings Perspective[J].Academy of Management Review,2001,26(2).