基于缩减策略的混沌时间序列LSSVM预测模型*

熊胜华，周翠英

(中山大学工学院，广东 广州 510275)

混沌时间序列的建模与预测是当今混沌理论研究的重要方向之一，而基于统计学习理论的最小二乘支持向量机(Least Squares Support Vector Machines，简称LSSVM)，由于其采用结构风险最小原则能最大程度地提高泛化能力和较好地解决非线性、高维数和局部极小值等实际问题，因此在混沌时间序列预测方面也具有较好的应用前景[1]。与传统的支持向量机(Support Vector Machines，即SVM)相比[2-3]，LSSVM把最优化问题中的求解二次规划问题转化为求解线性方程组问题，提高了算法的计算速度。但针对混沌时间序列的大样本学习，LSSVM法与SVM法一样，具有内存开销大、训练速度慢等缺点。因此，为了解决大样本学习的问题，许多学者对此开展了研究，主要研究可以概述为二类：

一类是利用某种缩减算法从整个大样本集的学习序列中找出少量的有效的支持向量集，去除大量的对样本学习贡献较少的非支持向量集，缩短支持向量机的训练时间。如：罗瑜等[4]提出了一种利用类别质心去除非支持向量对应的样本，缩小样本集的方法，该方法在不损失分类正确率的情况下具有更快的收数速度；杨晓伟等[5]针对最小二乘支持向量机丧失稀疏性的问题，提出了一种高效的剪枝算法，在训练的过程中，根据一些特定的剪枝条件利用块增量学习和逆学习交替进行的方法自动形成一个小的支持向量集，并利用此集合构造最终的分类器；骆世广等[6]考虑到SMO(Sequential Minimal Optimization，序贯最小优化)算法对大样本数据训练速度比较慢的问题，根据在SVM的优化过程中并不是所有样本都影响优化进展的思路，提出了两种删除样本的策略，一种是基于距离，另一种是基于拉格朗日乘子的值，从而大大缩短SMO的训练时间；另外还有田新梅等[7]、李红莲等[8]也做出过相应的研究。

另一类是利用某种分组算法将大样本的训练集进行细分，从而减少支持向量机每一次的存储空间和计算时间，再利用带有记忆功能的块增量学习法进行整体学习，从而达到缩短支持向量机的整体训练时间的目的。如：张浩然等[9]根据分块矩阵计算公式和核函数矩阵本身的特点设计了支持向量机的增量式学习算法和在线学习算法，该算法能充分利用历史的训练结果，减少存储空间和计算时间；张永等[10]基于数据分割和邻近对策略，利用c-均值聚类分别对数据集中的正负类进行聚类，把大数据集分割成互不相交的子集合，然后来自正负类的子集合两两组合形成多个二分类问题，并用SMO算法求解，最后用邻近对策略对未知数据进行识别；Boser B等[11]提出了一种选块算法解决大样本数据下SVM的训练速度问题，利用若干任意样本构成小规模训练集求解二次规划问题,得到一组支持向量，再将这些支持向量并入其它若干样本中再次训练，又得到一组支持向量，循环这个过程，直到所有样本都计算完毕。

综上所述，无论采用哪一类方法都可以达到减少大样本训练时间的目的，但也都存在一些不足：第一类方法的训练精度过分依赖于有效的支持向量集的选择，如果缩减算法选择不当，所选择的支持向量集并不能概括大样本训练集的重要发展规律，从而影响支持向量机的训练精度；第二类方法精度在于分组算法的选择，如果选择不当，同样对支持向量机的训练精度产生较大的影响。因此为了结合两类大样本的支持向量机快速算法的优点，同时为了克服它们的不足，本文提出一种针对混沌时间序列的基于新的缩减策略的LSSVM预测模型：该模型利用混沌时间序列的平均周期将大样本数据分解成不同的子集，将最后一个子集之外的其他子集利用拉格朗日乘子的值缩减一部分非支持向量，并将缩减后样本与最后一子集进行合并，利用相关系数缩减法缩减合并后的样本集，并利用最小二乘支持向量机方法进行回归预测。

1 基于缩减策略的混沌时间序列的LSSVM预测模型的构建方法

设样本训练集，(x1,y1),...,(xi,yi),...(xn,yn)，其中xi∈Rm,yi∈R,i=1,...,n，xi为输入向量，yi为输出向量。

混沌时间序列的预测问题主要是解决函数回归估计问题，它是通过对训练集训练后找到一个函数f，使得对训练集以外的任一测试样本xd，能够找到与其对应的yd=f(xd)，并使yd与其真值y的偏差最小。

在回归估计问题方面，LSSVM方法在非线性、高维数和局部极小值等实际问题具有明显的优点。在LSSVM原理中，它采用如下形式的函数对未知函数进行估计[12-14]：

y(x)=wTΦ(x)+b

(1)

其中Φ:Rm→H,Φ称为特征映射，H称为特征空间，w这空间H中的权向量，b∈R为偏置。为了有效地解决上述回归估计问题，LSSVM通过引入损失函数将回归估计问题转化为损失函数的风险最小化问题，同时采用结构化风险最小原则进行风险最小化分析，得出如下优化问题[12-14]：

(2)

约束条件：

yk=wTΦ(xk)+b+ekk=1,2,…,n

(3)

式中，γ为可调正则化参数，ek为误差变量。

由于直接求解(2)比较困难，因此采用对偶理论求解并建立Lagrange方程：

(4)

其中αi为Lagrange乘子，优化条件为[7]

(5)

为了求解(5)式，在LSSVM原理中，根据Mercer条件认为存在核函数K(xk,xl)，使得

K(xk,xl)=ΦT(xk)Φ(xl)

(6)

求解优化条件式(5)，消去w与ei，并将K(xk,xl)替换ΦT(xk)Φ(xl)，最终将优化问题转化为求解一个线性方程组：

(7)

其中为αi为拉格朗日(Lagrange)乘子,如果拉格朗日乘子的绝对值非常小，则对模型的回归贡献非常少，其对应的样本称为非支持向量，其他情况下拉格朗日乘子所对应的样本称为支持向量。

LSSVM算法采用最小二乘法求解式(7)表示的线性方程组，避免了标准支持向量机算法中求解凸二次规划问题，比传统的支持向量机方法具有更快的训练速度和更优的预测性能。因此，在求解混沌时间序列问题时采用LSSVM算法解决非线性回归问题。

本文通过对大样本混沌序列数据特性的分析，根据样本集分割与样本相关性的思想，建立了混沌时间序列的LSSVM预测模型，其构建方法表述如下：

1) 重构相空间，建立混沌时间序列的学习样本集及测试样本集：重构相空间是混沌时间序列的基础，其关键是求出混沌时间序列的嵌入维数m以及时延τ。目前来说，单独求时延方法有自相关法[15]、互信息法等[16]，单独求嵌入维的G-P 算法或FNN(Flase Nearest Neighbors)法等[17-18]；同时求时延与嵌入维的方法有嵌入窗法[19]、C-C 方法等[20]。本文采用C-C法同时求嵌入维与时延。假设混沌时间序列表示为{x1,x2,x3,…,xn}，其中，xi为混沌时间序列的实际值。求得的嵌入维数为m以及时延为τ，则重构相空间后得到的样本集如式(8)所示：

(8)

2) 利用快速傅立叶变换求解混沌时间序列的平均周期T，利用平均周期将大样本学习数据集分解成多个不同的样本子集，样本子集个数为n，每个样本子集的个数最大为T/m的取整数；

3) 初始选取正则化参数C及核参数δ，也可以通过多次组合比较预测结果来选取合适的正则化参数C及核参数δ；

4) 对子集序号为1到n-1的样本子集建立不同的LSSVM模型，利用拉格朗日乘子|αi|<θ1时对模型的回归贡献非常少的原理，从对应的样本子集中缩减其对应的非支持向量；并将缩减后的样本子集与最后一个样本子集合并构成新的学习样本集X′；

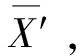
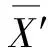
(9)

(10)

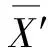
7)利用相关系数缩减法缩减相关距离|di′| <θ2的对应学习样本，将余下样本组成新的学习样本集Xend；

8) 利用初始选取的正则化参数C及核参数δ对学习样本集Xend建立LSSVM回归模型，对测试样本集进行非线性回归分析，最终输出相应的预测结果。

9) 为了衡量算法的预测精度，对测试数据采用均方误差MSE作为评价标准：

(11)

2 仿真实验及结果分析

实验一：采用典型的混沌时间序列Lorenz方程验证本模型[21]：

σ=16r=45.92b=4

(12)

取初始值为(-1，0，1)，积分步长为0.01，利用四阶Runge-Kutta算法求出Lorenz方程的数值解，为了从其数值解中取出具有明显混沌特性的数据点，本文正是从8 000个数据点后取出5 000个数据点进行仿真实验。

将取出的5 000个数据点的x分量进行预测分析，其中前4 000个数据点的x分量作为训练数据，后 1 000个数据点的x分量作为测试数据。其混沌时间序列的LSSVM预测模型的建立过程可描述如下：

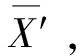
图1 Lorenz函数的混沌时间序列的预测图

将标准LSSVM模型对本文数据进行同样的预测，其模型的初始化正则化参数C=100及核参数δ=10，将其预测结果与本文模型进行比较，比较结果如表1所示。

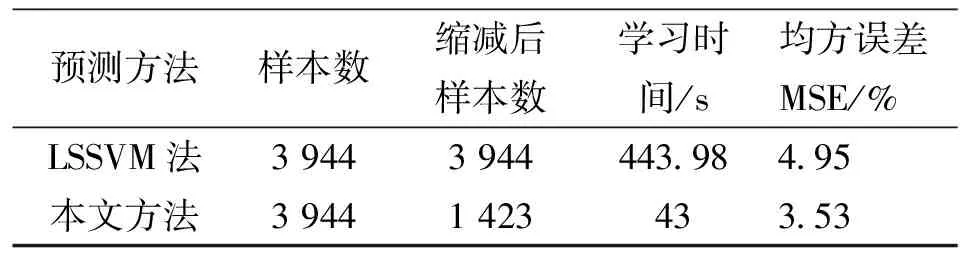
表1 Lorenz函数的混沌时间序列预测结果对照表

实验二：具有混沌特性的Mackey-Glass时滞微分方程定义为[21]

a=0.2,τ=17,b=0.1

(13)

本文取初始值为1.2，步长取0.1，通过四阶龙格-库塔方法求解产生混沌时间序列，从2 000个数据点后取出5 000个数据点进行仿真实验。

将取出的5 000个数据点的x分量进行预测分析，其中前4 000个数据点的x分量作为训练数据，后1 000个数据点的x分量作为测试数据。其混沌时间序列的LSSVM预测模型的建模过程与实验一类似，其预测结果图如图2所示。

图2 Mackey-Glass函数的混沌时间序列的预测图

将标准LSSVM模型对本文数据进行同样的预测，其模型的初始化正则化参数C=100及核参数δ=10，将其预测结果与本文模型进行比较，比较结果如表2所示。

表2 Mackey-Glass函数的混沌时间序列预测结果对照表

从两个不同实验的混沌时间序列预测结果对照表可以看出，与标准的LSSVM预测模型相比，本文模型在选择合适的临界参数θ1、θ2后，大大缩减了原始的学习样本，使模型学习速度得到大大提高，同时保证了预测精度基本不损失，有时会反而更好。这为混沌时间序列的预测提供了一种新的快速途径。

3 结 论

最小二乘支持向量机是一种基于统计学习理论，采用结构风险最小原则，具有较强的泛化能力的机器学习方法，在混沌时间序列预测方面具有较好的应用前景。但针对大样本数据的学习，最小二乘支持向量机方法具有内存开销大、训练速度慢等缺点。因此，本文通过对大样本混沌序列数据特性的分析，根据样本集分割与样本相关性的思想，建立了基于缩减策略下的混沌时间序列的LSSVM模型，通过相应的仿真实验验证了本模型可以在预测精度基本不损失的基础上具有较快的计算速度，为大样本的混沌时间序列的问题研究与预测提供了一种新的途径。通过研究得到以下两点认识：

1)混沌时间序列的预测问题，只要预测方法选择合适，预测参数选择合理，可以同时得到较好的预测效果和较快的计算速度；

2)本文模型充分利用了最小二乘向量机具有较强的推广预测能力和较好的预测精度的特点，且采用了样本集分割与样本相关性的思想，使其在基本不损失预测精度的基础上大大提高了其计算速度，通过实例证明本模型的实用性。

参考文献：

[1] 江田汉, 束炯. 基于LSSVM的混沌时间序列的多步预测[J]. 控制与决策, 2006, 21(1):77-80.

[2] 刘德地, 陈晓宏. 基于偏最小二乘回归与支持向量机耦合的咸潮预报模型[J]. 中山大学学报：自然科学版, 2007,46 (4): 89-92.

[3] 陈振洲, 李磊, 姚正安. 基于SVM的特征加权KNN算法[J]. 中山大学学报：自然科学版, 2005,44 (1): 17-20.

[4] 罗瑜, 易文德, 王丹珠,等. 大规模数据集下支持向量机训练样本的缩减策略[J]. 计算机科学, 2007, 34(10): 211-213.

[5] 杨晓伟, 路节, 张广全. 一种高效的最小二乘支持向量机分类器剪枝算法[J]. 计算机研究与发展, 2007, 44(7): 1128-1136.

[6] 骆世广, 骆昌日. 加快SMO算法训练速度的策略研究[J]. 计算机工程与应用, 2007, 43(13):184-187.

[7] 田新梅, 吴秀清, 刘莉. 大样本情况下的一种新的SVM迭代算法[J]. 计算机工程, 2007, 33(8): 205-207.

[8] 李红莲, 王春花, 袁保宗. 一种改进的支持向量机NN-SVM[J]. 计算机学报, 2003, 26(8): 1015-1020.

[9] 张浩然, 汪晓东. 回归最小二乘支持向量机的增量和在线式学习算法[J]. 计算机学报, 2006, 29(3): 400-406.

[10] 张永, 杨晓伟. 基于数据分割和近邻对的快速SVM分类算法[J]. 科学技术与工程, 2007, 7(21): 5563-5566.

[11] BOSER B, GUYON I, VAPNIK V. A training algorithm for optimal margin classifiers[C]∥Haussler D. Proceedings of the 5th Annual ACM Workshop on Computational Learning Theory. ACM Press, 1992.

[12] 董瑶, 潘国峰, 夏克文,等. 一种改进的LS-SVM算法及其应用[J]. 石油地球物理勘探, 2007, 42(6): 673-677.

[13] 夏克文, 董瑶, 杜红斌. 基于改进PSO算法的LS-SVM油层识别模型[J]. 控制与决策, 2007, 22(12): 1385-1389.

[14] 王旭辉, 黄圣国, 曹力, 等. 基于LS-SVM的航空发动机气路参数趋势在线预测[J]. 吉林大学学报：工学版, 2008, 38(1): 239-244.

[15] KANTZ H,SCHREIBER T. Nonlinear time series analysis[M]. Cambridge: Cambridge University Press, 1997.

[16] FRASER A M,SWINNEY H L. Independent coordinates for strange attractors form time series[J]. Phys Rev A，1986, 33: 1134-1140.

[17] GRASSBERGER P,PROCACCIA I. Measuring the strangeness of strange attractors[J]. Physica D, 1983, 9: 189-208.

[18] KENNEL M B,BROWN R,ABARBANEL H D I. Determining embedding dimension for phase-space reconstruction using a geometrical construction[J]. Phys Rev A, 1992, 45: 3403.

[19] KUGIURMTZIS D. State space reconstruction parameters in the analysis of chaotic times series-the role of the time window length[J]. Physica D, 1996, 95: 13-28.

[20] KIM H S,EYKHOLT R,SALAS J D. Nonlinear dynamics delay times and embedding windows[J]. Physica D, 1999, 127: 48-60.

[21] 王永生, 范洪达, 尚崇伟, 等. 混沌时间序列的神经网络预测研究[J]. 海军航空工程学院学报， 2008, 23(1): 21-25, 32.