含非线性色散项的Kadomtsev-Petrishvili方程的破缺行波解*

高正晖，杨 柳

(衡阳师范学院数学与计算科学系，湖南 衡阳 421008)

自1981年Konno等[1]首次报告非线性振动模型存在环状孤波解以来，引起了许多学者对非线性发展方程环状孤波解的关注，现已发表了一些关于非线性发展方程的环状孤波解的学术论文[2-4]。近年来，李继彬[5-8]，刘正荣[9-10]等运用动力系统的分支理论对一些非线性发展方程的行波解的动力学行为进行了研究，发现一些非线性发展方程的环状孤波解不是一个真正的解，它是由三个破缺行波解所组成，并给出了一些非线性发展方程破缺行波解的参数表示。

1970年，Kadomtsev等[ 11-12 ]首次提出如下二维的KdV方程，即KP方程

(ut+uux+uxxx)x+εuyy=0

(1)

它是一个重要的非线性偏微分方程, 该方程有着广泛的物理背景，常用来描述二维小振幅弱色散波，如二维浅水波、未磁化等离子体声波等，在流体力学、等离子体物理、气体动力学等领域有重要的应用，对它的深入研究将有利于实际物理问题的解决。本文的目的是对含非线性色散项的Kadomtsev-Petrishvili方程

(ut+uux+(u2)xxx)x+εuyy=0

(2)

进行研究，运用动力系统分支理论对方程(2)的行波系统的动力学行为进行分析，根据这些分析，我们也获得了该行波系统存在环状孤波解，它也是由三个破缺行波解所组成，并给出了破缺行波解的参数表示。

1 行波系统的分支相图

对于方程(2)，我们作如下行波变换:ξ=x+ay+βt,u(x,y,t)=φ(ξ)，其中α,β为待定常数。由此方程(2)约化为常微分方程

(βφ′(ξ)+φ(ξ)φ′(ξ)+(φ2(ξ))‴)′+

εα2φ″(ξ)=0

(3)

对(3) 式积分并取积分常数为0，得

βφ′(ξ)+φ(ξ)φ′(ξ)+(φ2(ξ))‴+

εα2φ′(ξ)=0

(4)

再对(4) 式积分并取积分常数为g，得

2φ′2(ξ)+2φ(ξ)φ″(ξ)=g

(5)

令φ′=v，并令λ=β+εα2，则可得以下平面自治系统(行波系统)

(6)

令dξ=2φdτ，则除奇异直线φ=0外，行波系统(6)与下面的可积系统有相同的拓扑结构

(7)

显然，行波系统(7)的首次积分是

(8)

对于行波系统(7)，其平衡点满足方程组

(9)

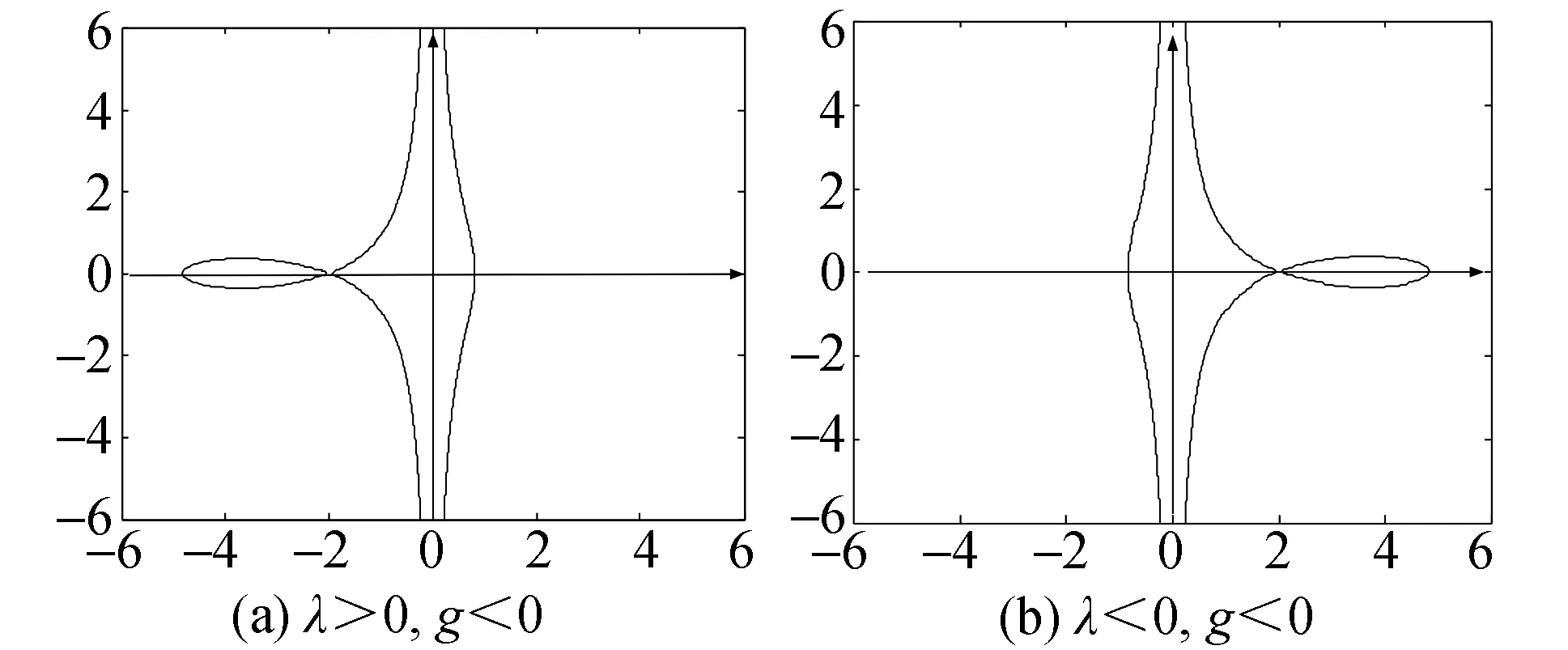
图1 行波系统(7)的平面相图

2 破缺行波解的参数表示

1)当Δ=λ2+2g>0且λ>0,g<0时，方程的破缺行波解的参数表示。

(11)

由(11)式可得

(12)

由此得到行波系统(6)由三个破缺行波解组成的环状孤波解

(13)

其中ξ0是积分常数。

因此，得

从而解得

由此得到行波系统(6)由三个破缺行波解组成的环状孤波解(如图2)的参数表示

(14)

图2 参数方程(14)的平面图

2)当Δ=λ2+2g>0且λ<0,g<0时，方程的破缺行波解的参数表示。

(15)

由此得到行波系统(6)由三个破缺行波解组成的环状孤波解

(16)

其中ξ0是积分常数。

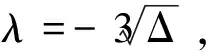
因此，得

从而解得

由此得到行波系统(6)的由三个破缺行波解组成的环状孤波解(如图3)的参数表示

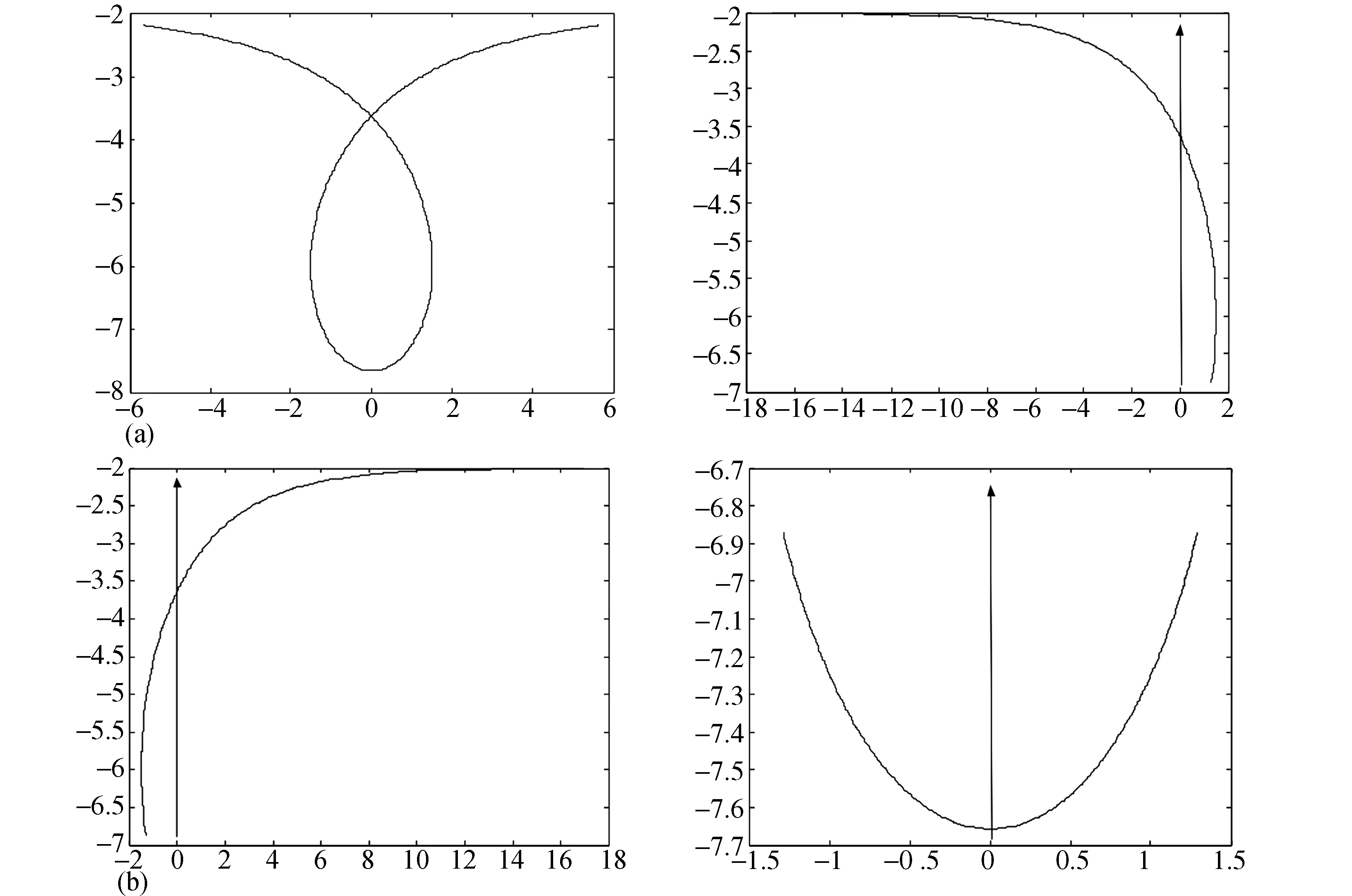
图3 参数方程(18)的平面图

(θ为参数)

(18)

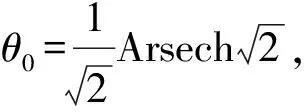
参考文献：

[1] KONNO K, ICHIKAWA Y H, WADATI M. A loop soliton propagating along a stretched rope [J]. J Phys Soc Japan, 1981, 50(3): 1025-1026.

[2] VAKHNENKO V O, PARKES E J. The two loop soliton solution of the Vakhnenko equation [J]. Nonlinearity, 1998, 11: 1457-1464.

[3] PARKES E J. Explicit solution of the reduced Ostrovsky equation [J]. Chaos, Solitons and Fractals, 2007, 37(3): 602-610.

[4] PARKES E J. Some periodic and solitary traveling-wave solution of the short-pulse equation [J]. Chaos, Solitons and Fractals, 2008, 38(1): 154-159.

[5] LI J B. Dynamical understanding of loop soliton solution for several nonlinear wave equations [J]. Science in China：A, 2007, 50(6): 773-785.

[6] LI J B. Family of nonlinear wave equations which yield loop solutions and solitary wave solutions [J]. Discrete and Continuous Dynamical Systems, 2009, 24(3): 897-907.

[7] 李继彬. 两非线性波方程真圈解的存在性和破缺性[J]. 应用数学和力学, 2009, 30(5): 505-514.

[8] LI J B, DAI H H. On the study of singular nonlinear traveling wave equations:dynamical approach[M]. Beijing: Science Press, 2007.

[9] 刘正荣, Ali Mohammed Kayed. 分支方法与广义CH方程的显式周期波解 [J]. 华南理工大学学报:自然科学版, 2007, 35(10): 227-232.

[10] 郭柏灵, 刘正荣. CH-r方程的尖波解[J]. 中国科学：A辑, 2003, 33(4): 325-337.

[11] KADOMTSEV B B, PETVIASHVILI V I. On the stability of solitary waves in weakly dispersive media [J]. Sov Phys Dokl, 1970, 15: 539-541.

[12] 郭柏灵. 非线性演化方程[M]. 上海: 上海科技教育出版社, 1995.