平原河网十字型汊口出入流断＊面污染物浓度响应关系研究

韩龙喜,陆 东,计 红

(1.河海大学水文水资源与水利工程科学国家重点实验室,江苏南京 210098;2.河海大学浅水湖泊综合治理与资源开发教育部重点实验室,江苏南京 210098;3.河海大学环境科学与工程学院,江苏南京 210098)

平原河网十字型汊口出入流断＊面污染物浓度响应关系研究

韩龙喜1,2,3,陆 东3,计 红3

(1.河海大学水文水资源与水利工程科学国家重点实验室,江苏南京 210098;2.河海大学浅水湖泊综合治理与资源开发教育部重点实验室,江苏南京 210098;3.河海大学环境科学与工程学院,江苏南京 210098)

在平原河网地区,十字型汊口是不同河道间实行水量与污染物交换的重要水域,而出、入流断面污染物浓度间的响应关系,是模拟平原河网水质时空变化的一个十分重要的技术参数。本文通过十字型水槽物理模型,对“两进两出”十字型汊口二维水动力、水质数学模型进行验证。结果表明,在“两进两出”十字型汊口不同出流断面的污染物平均浓度存在较大差异。在此基础上,提出了新的该类型汊口出入流断面污染物平均浓度间的响应关系,给出了响应系数计算公式。将利用本文方法得出的响应系数与常用的三级联解法基于“汊口污染物均匀混合假设”得出的响应系数进行了对比,突显了三级联解法的误差。本文的研究成果可为平原河网水质模拟方法的改进提供依据。

河网;十字型汊口;污染物浓度;响应关系

平原河网中河流交汇现象十分普遍,许多单一河道由汊口 (交汇点)相互连接形成河网系统。目前,数学模型仍然是研究平原河网地区污染物浓度的时间、空间分布规律的一个不可或缺的重要工具。一般来说,汊口污染物迁移特征十分复杂,而汊口出流断面与入流断面污染物浓度间的响应关系,是河网水质数学模拟的一个关键技术问题。在现有的平原河网水质模拟方法中,三级联解法是最为常用的方法,而该方法在处理汊口处污染物混合扩散这一关键问题时,主要采用“均匀混合假设”——流入汊口的污染物在汊口充分混合达到均匀程度,故汊口所有流出断面的污染物平均浓度均等于入流断面污染物充分混合后的浓度[1-2]。显然,此假设有一定的适用范围——连接汊口河道为“一进多出”或 “多进一出”。而实际上,平原河网地区汊口河道以 “两进两出”最为常见,由于达到均匀混合所需纵向距离较长[3-4],或流入汊口的河道污染物浓度差异较大时,污染物根本不能达到均匀混合,假设必然带来系统误差。因此,应充分考虑汊口出流断面浓度的不均匀性,并研制与之相匹配的平原河网水质模型[5]。

本文采用物理模型和数学模型相结合的方法研究“两进两出”十字型汊口流体的水动力特性和污染物平面二维分布特征。在此基础上,提出了新的该类型汊口出、入流断面的污染物浓度响应关系,给出了响应系数计算公式。构造典型算例,将所得结果与常用的 “汊口污染物均匀混合假设”的相应结果进行对比,突显了 “均匀混合假设”的系统误差。本文研究成果可为平原河网水质模拟方法的改进提供技术依据。流流量为 0.61 L/s,水槽 A出流流量为 0.82 L/s,水槽B入流流量为 0.61 L/s,水槽 A出流水深为6.6 cm;工况二:水槽A入流流量为 0.49 L/s,水槽A出流流量为 0.85 L/s,水槽 B入流流量为0.73 L/s,水槽 A出流水深为 6.6 cm。水槽模型尺寸及测点布置见图 1。

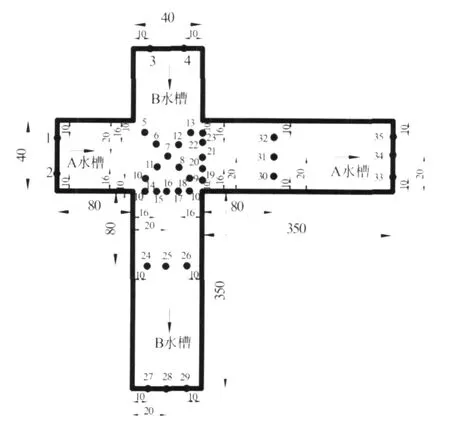
图 1 水槽模型尺寸和测点布置图 (单位:cm)Fig.1 Sizes of flume model and distribution ofmeasurement points

1 汊口水动力学特性研究

1.1 汊口水动力特性试验设置

1.1.1 物理模型设计 采用室内水槽模拟河道的水流、污染物输运特征。物理模型试验成果按一定的比尺换算后,可用于水动力数值模拟结果的率定和验证。根据试验场地及供水条件,采用变态比尺设计水槽模型,水平比尺为 100∶1;垂向比尺为30∶1[6-7]。具体模型尺寸及流速测点布置见图 1。共布置了 10个监测断面 35个测点,其中,在掺混剧烈的汊口处测点较密集,共布置了 4个监测断面,19个测点。

1.1.2 物理模型试验工况 对汊口入流、出流水动力条件设置了 2种试验工况,研究分析汊口水动力特征。共有 2种试验工况,工况一:水槽 A入

1.2 汊口水动力数值模拟

1.2.1 控制方程 平原河网地区河流一般为宽浅型,可采用水深平均的平面二维水动力数学模型数值模拟垂线平均流速的平面分布。通过求解黎曼问题计算汊口流场[8]。

1.2.2 边界条件 根据物理模型几何相似率,得到流速比尺为 5.48,流量比尺为 16 640,据此对物理模型两种工况下的入流、出流边界条件进行换算,得到数学模型模拟的原型河道的水动力边界条件。

1.2.3 网格剖分 采用均匀矩形网格,网格大小设定为 4 m,计算域为两条各为长 920 m,宽 40 m的十字交叉形河道,其中汊口上游 80 m,下游 800 m。共 4 500个计算单元,4 591个计算节点。

1.2.4 水动力模拟结果分析 依据流速比尺,将水槽物理试验结果换算成相应的原型河道水流流速,采用工况 1物理试验数据对汊口二维水动力模型进行率定,采用工况 2进行验证。流场率定结果见图 2(a),验证结果见图 2(b)。由模型率定、验证结果对比可见,流速相对误差小于 30%的占80%以上,计算流场与实测流场基本一致。

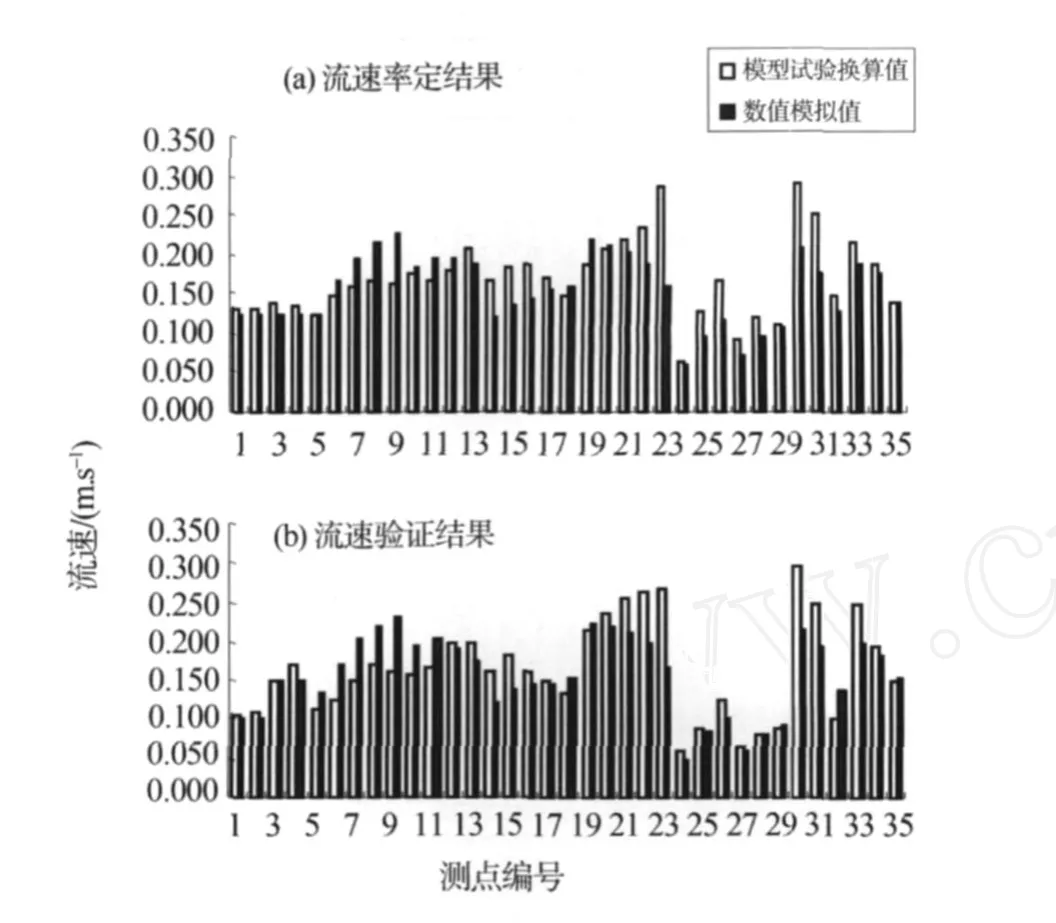
图 2 模型率定及验证时水槽试验及数值模拟流速对比Fig.2 Comparison of velocity between physical and mathematicalmodels in confirmation and validation

1.3 试验结果及计算结果对比分析

本文仅给出工况 2数值模拟及物理试验流场(见图 3)。由图 3可知,对于汊口入流河道,流线基本顺直,流场受汊口影响相对较小;对于汊口,流速的流向、大小具有很大的空间分布不均匀性,表现为流向急剧变化,最大变幅近 90°,流速差异较大,具体表现为近岸流速较小,汊口中心流速较大;而对于汊口出流河道,由于受到汊口水流流态的影响,靠近汊口的出流断面水流流速呈现出较大的不均匀性,具体表现为水流流向沿横断面方向存在较大的切变,流速大小沿横断面分布也很不均匀:临近入流断面一侧流速较小,远离入流断面一侧由于两入流断面水流的挤压及水流的惯性作用,流速相对较大。随着水流向下游流动,水流在东面分布上的差异特征逐步消失。

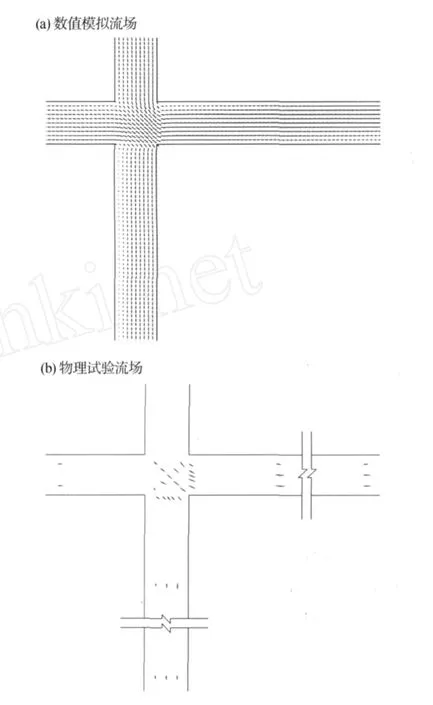
图 3 工况 2数值模拟及物理试验流场Fig.3 Flow fields bymathematicalmodel and by physicalmodel

2 汊口扩散质输运规律研究

2.1 汊口扩散质输运规律试验研究

进行污染物在水体中的对流扩散的模型试验时,需考虑所研究的扩散物质在不同比尺水体中的对流扩散相似规律,这样才能较为准确的将模型试验数据推广到原型水体中。王美敬等[9-10]在水动力学条件相似的基础上,推导出了污染物扩散-降解模型所遵循的相似准则并进行了验证,结果表明:在具有明显二维特征的原型与模型试验中,模型所获得成果可较好地应用到实际河流中。本文借鉴前人的研究成果采用适当的相似条件进行汊口污染物扩散的物理模型试验。

2.1.1 试验工况 水流工况分 2种:工况 1和工况2。

2.1.2 示踪剂及浓度设定 试验中利用碳素墨水作为示踪剂,通过浊度仪测量透光度作为流体中污染物的当量浓度值。在A水槽中投放示踪剂,B水槽进水为清水。设定清水中示踪剂的浓度为 0,投放的示踪剂碳素墨水浓度设为 6。

2.2 汊口扩散质输运数值模拟

应用平面二维对流扩散方程描述污染物的输运扩散,通过求解黎曼问题得到污染物垂线平均浓度在平面上的分布特征。

2.2.1 控制方程

式中,h为水深;u、ν分别为x、y方向垂线平均水平流速分量;Ci为污染物的垂线平均浓度;Eix、Eiy分别为x、y方向各污染物的扩散系数;KCi为污染物综合降解系数。

2.2.2 定解条件 给定初始条件为c(x,y,0)=c0(x,y),对岸边界采用边界不可入条件,入流边界给出各节点的污染物浓度,出流边界采用第二类边界条件,即=0。网格的布置同流场计算。计算浓度时两个上游入口边界给定浓度同物模试验,A河道上游边界浓度为 6,B河道上游边界浓度为0。纵向扩散系数Ex、Ey由经验公式确定[11]。污染物降解系数KCi取为 0(不考虑降解)。

2.3 试验、计算结果对比及汊口浓度分布分析

本文仅给出工况 1物理试验、数值模拟的示踪剂浓度场 (见图 4)。根据所有观测点上物理试验数据、数值模拟结果的统计分析可知,观测浓度与数值模拟结果差值小于 1mg/L的点据占 83%,计算浓度场与实测浓度场基本一致。

根据工况 1、2示踪剂浓度平面分布的物理试验、数值模拟结果可知,在汊口区域,示踪剂浓度沿水流运动的法向,存在较大的浓度梯度,靠近低浓度入流河道一侧汊口水域浓度相对较低,反之则较高。且由于流程较短,示踪剂在汊口混合程度较低,因此,相应地导致了不同出流河道断面平均浓度的巨大差异,即紧邻低入流浓度河道的出流河道,由于其来水组成大部分为低浓度来水,因此该出流断面示踪剂浓度相对较低,而紧邻高入流浓度河道的出流河道,由于其来水组成大部分为高浓度来水,因此出流浓度相对较高。

3 出入流断面浓度响应关系分析

汊口出流断面的平均浓度与汊口流入断面的污染物平均浓度间的响应关系,是平原河网水质模拟的关键技术。本文提出基于汊口污染物非均匀混合的出入流断面浓度响应系数的求解方法,并构造典型算例采用本文的计算方法计算响应系数,然后与常用的基于均匀混合假设的三级联合解法的响应关系进行比较分析。

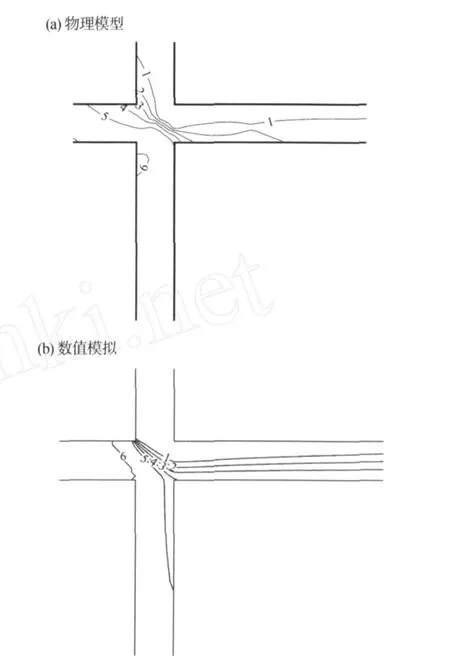
图 4 工况 1物理模型及数值模拟示踪剂浓度场Fig.4 Concentration field bymathematicalmodel and by physicalmodel

3.1 均匀混合假设概述

假设有如图 5所示的 “两进两出”十字型汊口 (图中箭头指向表示水流方向),Q1、Q2分别为 A河道、B河道的入流流量,C1、C2为相应的入流污染物质量浓度;Q3、Q4为 A河道、B河道的出流流量,C3、C4为相应的出流污染物质量浓度。

均匀混合假设认为,所有汊口出流断面的污染物平均浓度,均等于汊口节点浓度——入流断面污染物在交叉点均匀混合后的浓度。数学表示为[1]:

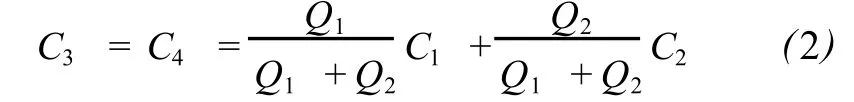
可将出流断面平均浓度简单表示为入流断面平均浓度的线性函数,有:

图 5 汊口污染物混合输运示意图Fig.5 Schematic illustration of pollutantmixing and transferring at joint nodes

3.2 非均匀混合假设响应关系数学表达

十字形汊口污染物非均匀混合条件下,出流断面浓度可表示为入流断面平均浓度的线性组合,数学表示为:

式中,α′1,α′2分别为河道 A出流污染物浓度对河道 A、B入流污染物浓度的响应系数,β′1,β′2分别为河道 B出口污染物浓度对河道 A、B入流污染物浓度的响应系数。

3.3 响应系数计算方法

天然河道进入汊口的污染物浓度通常不等,不妨假设C2＜C1,令C2=Cb,则C1可表示为C1=Cb+△C,代入式 (5)、(6)得:

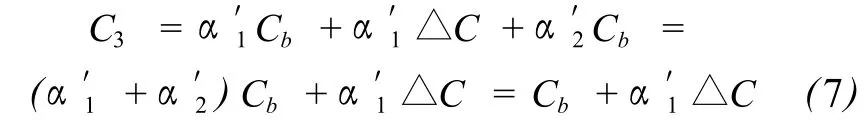
A河道入流断面污染物浓度与B河道相比存在变幅△C,不妨设由此在A河道出流断面产生的相应浓度增量为△C3,在 B河道出流断面产生的相应浓度增量响应为△C4。则有:C3=Cb+△C3,C4=Cb+△C4。将此关系带入到方程 (7),得到:

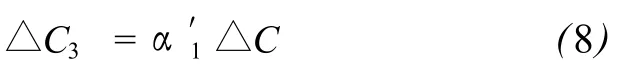
同理可得,

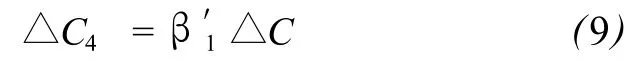
由式 (8)、(9)得:

式中,B3为A河道出流断面的宽度,B4表示B河道出流断面的宽度。u(b)、h(b)、c(b)分别表示出流河道断面的流速、水深及垂线平均浓度沿横向的分布,可由上述汊口平面二维数值模拟计算得到。

3.4 典型算例响应系数对比

计算了 3种典型算例的出流断面污染物浓度响应系数,并与基于均匀混合假设的响应系数进行了对比,结果见表 1。

表 1 响应系数对照表Table1 Comparison of response coefficients be tween different hypotheses

由表 1可知,出流河道的浓度响应系数与入、出流河道的流量分配有关。基于均匀混合假设的响应系数与基于非均匀混合理论的响应系数相比,在数值上存在较大的偏差。

4 小 结

1)水槽试验及数学模型模拟结果显示,十字型汊口水域,由于受到进入汊口水体污染物浓度差异的影响,扩散质掺混很不均匀,污染物浓度在汊口存在很大的浓度梯度,出流断面污染物浓度沿横向的分布存在显著差异。

2)提出了汊口出流断面平均浓度对入流断面污染物平均浓度的响应系数的计算方法,研究结果表明,不同出流断面的污染物浓度响应系数不等。

3)研究结果对比表明,基于汊口污染物均匀混合假设的出流断面浓度响应系数存在较大偏差。在进行平原河网水质模拟时,应考虑入流断面水质不均匀性对流出汊口水质的影响,研制更为合理的平原河网水质模型。

[1]韩龙喜,朱党生 .河网地区水环境规划中的污染源控制方法[J].水利学报,2001(10):28-31.

[2]吴作平.河网水流数值模拟方法研究 [J].水科学进展,2003,14(3):350-353.

[3]张书农.环境水力学 [M].南京:河海大学出版社,1988:134-139.

[4]CHO I G W,MOL INAS A.Simultaneous solution algorithm for channel network modeling[J].Water Resource,1993,29(2):321-328.

[5]韩龙喜,陆冬.平原河网水流水质数值模拟研究进展[J].河海大学学报:自然科学版,2004,32(2):127-130.

[6]汪德胜 .水力变态模型相似律问题的探讨[J].泥沙研究,1987(4):72—79.

[7]郑国栋,郑邦民.变态模型水流相似的精度及误差分析[J].水动力研究与进展,2005,20(1):33-37.

[8]胡四一,谭维炎.一维不恒定明流计算的三种高性能差分格式[J].水利学报,1991,2(1):11-21.

[9]王美敬,罗麟.水中污染物扩散模型实验中的相似理论[J].四川大学学报:工程科学版,2004,36(2):25-28.

[10]王美敬,罗麟,黄小雪 .污染物横向扩散在变态模型与河流中的相似性[J].四川大学学报:工程科学版,2006,38(4):15-18.

[11]李锦秀,黄真理,吕平毓 .三峡库区江段纵向离散系数研究[J].水利学报,2000(8):89-94.

Response Relation of Pollutant Concentration Between Outlet and Inlet Sections at Joint Nodes of Pla in River Network

HAN Longxi1,2,3,LU Dong3,JI Hong3
(1.State KeyLaboratory of Hydrology-Water Resource and Hydraulic Engineering,Nanjing 210098,China;2.KeyLaboratory of Integrated Regulation and Resource Development on Shallow Lakes,MOE,Nanjing 210098,China;3.College of Environmental Science and Engineering,HohaiUniversity,Nanjing 210098,China)

In plain river ne twork,joint nodes can not be ignored for exchange of water flow and pollutants from differentwatercourses.Response relation between outlet sections and inlet sections is an important technical parameter forwater quality simulation.Aiming at the response relation research of crossed joint nodeswith two inlet sections and two outlet sections,thispaper builds2-D hydraulic andwater qualitymathematicalmodels and validates them by physical models.The results show that pollutant concentration differs greatly for different outlet sections.Based on the work above,a new expression of response relation and calculating equations of response coefficients are put for ward.By comparing the response coefficientswith those inferred from even mixing hypothesis mainly used in three-step method,obvious errors caused by even mixing hypothesis are disclosed.This study helps to improve the simulation method of plain river network water quality.

plain river network;crossed joint nodes;pollutant concentration;response relation

TU991

B

0529-6579(2011)01-0123-06

2009-11-16

水利部公益性行业科研专项经费资助项目 (201001028)

韩龙喜 (1964年生),男,教授;E-mail:hanlongxi@sina.com