一种滚动轴承故障知识获取的新方法

乔保栋，陈果，葛科宇，曲秀秀

(南京航空航天大学 民航学院，南京 210016)

滚动轴承的运行状态往往直接影响到整台机器的精度、性能、可靠性及寿命等，因此，对轴承的状态监测与故障诊断具有重要意义[1]。轴承故障诊断有多种方法，其中振动法由于其适用性强、效果好、测试及信号处理简单直观而被广泛应用。振动信号的时域参数可以实现对轴承的简易诊断，即判断轴承是否存在故障。要精确判断轴承故障发生在哪个元件上，就需进行频域分析。轴承故障信号具有信号微弱、调制性强以及频带范围宽等特征，目前小波变换已被广泛应用于轴承故障诊断[2-3]。Hilbert-Huang变换中的EMD具有自适应性、正交性与完备性及IMF分量的调制特性等突出特点，目前已有许多研究者将Hilbert-Huang变换应用于轴承故障诊断[4-5]。如何综合运用时域和频域方法，并对大量信息进行处理和综合利用轴承故障诊断技术是需要重点研究的问题。诊断的核心问题是模式识别，包括模式获取和模式匹配两个过程，轴承故障诊断的主要问题是故障特征模式提取，也就是知识获取的问题[6]。

有鉴于此，文中对数据挖掘技术在轴承故障诊断中的应用进行了探索，从大量的轴承振动信号中获取能够反映轴承运行状态的时域参数和小波包络谱特征参数，建立基于Weka平台知识获取的故障智能诊断方法，对轴承的故障进行诊断。

1 故障特征参数选取

1.1 时域参数

一般来说，安装在轴承座上的传感器拾取到的轴承振动信号是一组宽带信号，随机性比较强。因此，可以通过轴承振动信号的时域参数所构成的特征向量来反映轴承的运行状态。目前，对轴承振动信号进行时域处理常用的参数指标主要有均方根值、峰值、峰值因子、脉冲因子、裕度因子、波形因子和峭度等。

1.2 轴承小波包络谱特征提取

由文献[8]得知，小波包络谱能够体现轴承的故障特征频率，为识别轴承故障部位提供重要判据。因此可以借助小波包络谱来自动获取其频率特征，从而为智能诊断提供征兆信息。

小波包络谱特征提取具体计算步骤为：

(1)按统一的采样频率进行重采样，使小波分解中尺度所代表的频率值相同。

(2)确定分解层数，通常取l=3。

(3)确定小波函数dbN，通常取N=8～10。

(4)进行小波分解，得到第3层各结点重构信号。

(5)对小波分解层的细节信号进行Hilbert变换，获得小波包络谱。

设包络谱为W(f)，F1为旋转频率包络谱值；F2为外圈包络谱值；F3为内圈包络谱值；F4为滚动体包络谱值；F5为保持架包络谱值。由于根据轴承转速和几何尺寸计算出的故障特征频率与实际包络谱中的故障特征频率总是存在差异，因此特征值需要在一定范围寻找。设其特征频率差异为δf，包络频谱间隔为Δf，令m=δf/Δf，则在l层中的细节信号各特征值为

(1)

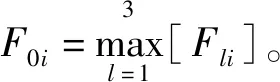
(7)对特征量进行归一化处理，即

(2)

2 基于Weka平台的轴承故障知识自动获取方法

Weka是新西兰Waikato大学开发的全面的数据挖掘系统[9]，它不仅提供了多种数据挖掘方法(分类、聚类及关联规则等)和常用算法，还提供了适用于任意数据集的数据预处理功能，以及算法性能评估的多种方法。文中主要采用C4.5决策树算法。

2.1 连续属性的离散

针对连续属性，C4.5算法主要通过下列途径来处理。设在集合T中，连续属性A的取值为{v1,v2,…,vm}，则在vi和vi+1之间的任意值都可以把训练集分成两个部分，即T1={t|A≤vi}，T2={t|A>vi}，因此总共有m-1种分割情况。对属性A的m-1种分割的任意一种情况，作为该属性的两个离散取值，重新构造该属性的离散值，再计算每种分割所对应的信息增益率。然后取最大增益率的分割作为属性A的分支，即threshold(V)=vk，其中vk对应的信息增益率为最大。

2.2 C4.5决策树算法

C4.5算法是一种有指导归纳学习的算法，继承了ID3算法的全部优点并对其作出了改进，其特点表现在以下几个方面：(1)采用信息增益率来选择属性，克服了用信息增益选择属性时偏向选择取值多的属性的不足；(2)不仅能处理离散值属性，而且能处理连续值属性；(3)能对不完整数据集(如个别属性值未知)进行处理；(4)降低错误修剪率；(5)提高计算效率等。

C4.5算法采用信息增益比来描述属性对分类的贡献,用以消除具有大量偏向值属性的偏差。设样本集T按类别属性A的s个不同的取值，划分为T1,…，Ts，共s个子集，则用A对T进行划分的信息增益为

(3)

式中：I(T)表示T的信息熵。设T中有m个类，则

(4)

式中：pj表示T中包含类j的概率。

用A对T进行划分的信息增益率为

Ratio(A,T)=Gain(A,T)/SplitInfo(A,T)，

(5)

|T|)。

(6)

采用此增益率去划分属性得到决策树,其中每个结点取具有最大信息增益率的属性。此方法简单高效、结论可靠,无需很强的相关知识。

具体的算法步骤如下：

(1)对训练样本samples各项属性数据进行预处理；

(2)创建根结点root，并确定attribute_lists叶结点属性；

(3)计算候选属性attribute_lists中每个属性，选取Gain-Ratio(X)最大且同时获取的信息增益Gain(X)属性又不低于所有属性平均值的属性作为测试属性；

(4)将当前选中的属性赋值给当前结点,将该属性的属性值作为该属性的分叉结点，并且将这些分叉结点插入队列中；

(5)从后选属性attribute_lists中将当前使用属性删除；

(6)从队列中取出一个结点，递归进行(3)到(5)步骤，直到候选属性attribute_lists为空；

(7)为每个叶子结点分配类别属性，对相同的类别属性进行合并，将其进行约减。

基于以上决策算法得到的决策树数据模型，在该模型中之所以选取信息增益率大而信息增益不低于平均值的属性，是因为高信息增益率保证了高分枝属性不会被选取，从而决策树的树形不会因某结点分枝太多而过于松散。

2.3 决策树的剪枝

当得到了完全生长的决策树后，为了消除噪声数据和孤立结点引起的分枝异常，需对决策树进行剪枝。决策树的剪枝是避免训练数据过分适应问题，其修剪方法通常利用统计方法删去最不可靠的分支，以提高分类识别的速度和数据准确分类的能力。

C4.5采用悲观错误修剪法，在用生成决策树的训练数据集来检验误判率时，实际上对错误的估计过于乐观，因为决策树是由训练数据集生成的，所以，在多数情况下决策树与训练数据集是符合的。但把决策树用于对训练数据以外的数据进行分类时，错误率将会增加。基于以上原因，Quinlan借用二项分布对训练数据中的误判率加以修正，以得到更为符合实际的错误率。与修正前的错误率相比，修正后的错误率增大了不少，因此认为它对错误率的看法是“悲观”的。

算法简化过程为：对决策树上所有非叶结点A进行计算分析。从树的根结点开始，计算每个分枝结点被剪也即被叶替代后的误判率。采用训练数据集作为测试集，取置信区间的上限作为对误判率的估计。给定一个显著性水平度α(C4.5算法中默认α=0. 25),显然错误的总数服从二项分布,则

(7)

式中：p为实际观测到的误判率，p=E/N；E为修剪后出现的错误实例树；N为被修剪的子树下的实例总数；pe为估计的误判率。

令z=u1-α，取置信区间的上限作为这个结点的误判率的估计，则该结点的误判率的计算式为

(8)

设定期望误判率的最大值为C，若剪枝后估计的误判率pe高于C时，则保留原来的分枝；否则剪去该分枝，用叶片代替。

2.4 决策树规则提取

决策树具有直观性和易理解等特点，可以直接从剪枝后生成的决策树中提取相应的决策规则。分类规则是用IF-THEN形式表示，每条规则都是一条从根到叶结点的路径。叶结点表示具体的结论，而叶结点以上的结点及其边表示相应条件的条件取值。从决策树到决策规则如图1所示。

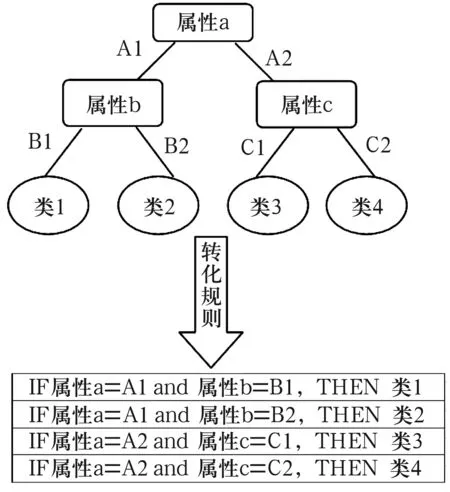
图1 决策树到规则转化

3 诊断实例

这里使用的轴承故障数据由文献[8]中的试验台采集得到。对轴承故障数据进行小波包络谱特征提取和时域参数指标提取，将小波包络谱特征值与时域参数指标值组成一组故障样本。表1为部分数据样本，由于样本数相对较少，试验中采用目前最流行的10折交叉验证准则(10-fold cross validation)来比较和评价算法。即将初始样本集划分为10个近似相等的数据子集，每个数据子集中属于各分类的样本所占的比例与初始样本中的比例相同，在每次试验中用其中的9个数据子集组成训练样本，用剩下的一个子集作为测试集，轮转一遍进行10次试验。最后获取的知识规则的决策树及其可视化形式如图2所示。

表1 滚动轴承部分样本

图2 weka平台C4.5决策树算法生成的决策树及其可视化形式

(1)规则1(K≤3.620 9)→轴承正常。这表示当峭度因子较小时，轴承正常，与文献[1]中结论一致， 峭度因子可以判断轴承是否异常。

(2)规则2(K>3.620 9&Fe>0.716)或(K>3.620 9&Fe≤0.716&Fi≤0.396 9&Fr>0.735 8)→轴承外圈故障。这表示当峭度因子较大且外圈故障特征值较大时，轴承外圈存在故障；或者当峭度因子较大而内、外圈故障特征值较小，并且旋转频率特征值较大时，轴承外圈存在故障。

(3)规则3(K>3.620 9&Fe≤0.716&Fi>0.396 9 )→轴承内圈故障。这表示当峭度因子较大，外圈故障特征值较小而内圈故障特征值较大时，轴承内圈存在故障。

(4)规则4(K>3.620 9&Fe≤0.716&Fi≤0.396 9&Fr≤0.735 8)→滚动体故障。这表示当峭度因子较大，同时内、外圈故障特征值，旋转频率特征值均较小时，滚动体存在故障。

轴承保持架故障之所以没有提取出规则，是因为整个152个样本中没有该类型的故障样本。表2为用10折交叉验证准则对提取出规则的验证结果。结果表明规则具有很高的精度，从而证明了该方法的有效性。

表2 规则验证的结果

4 故障试验分析

某研究所设计制造的转子-滚动轴承故障试验器能有效地模拟转子-轴承系统的转子不平衡及轴承常见故障。该故障试验器包括转轴、转子圆盘、轴承座、调速电动机、齿轮增速器以及综合电子控制系统。转轴两端由待检测轴承支承，轴承型号是6304，将加速度传感器安装在待检测轴承的轴承座上。振动加速度信号通过NI USB9234数据采集卡采集得到，采样频率为10 kHz。轴承损伤采用线切割加工，分别在外圈和内圈滚道加工了一个宽度为0.6 mm的裂缝，用以模拟滚道损伤所产生的冲击。

采集42组正常轴承数据，提取每组振动数据的时域峰值因子、峭度因子、脉冲因子及裕度因子，同时对每组振动数据进行小波包络谱特征提取，将以上参数组成一组特征向量，用上面得出的知识规则进行诊断，识别结果如图3所示。从图3a中可以看出，大多数样本都位于峭度标准线以下，而只有两个在标准线以上，表明峭度值可以很好地判断轴承是否发生异常。此时，42组正常轴承的样本数据正确识别率达92.8%，其中将正常轴承误识别为外圈故障的比率为2.4%，将正常轴承误识别为内圈故障的比率为4.8%。

图3 正常轴承测试结果

采集13组轴承外圈故障数据，应用上述方法，识别结果如图4所示。由图4可以看出轴承外圈有故障时，通常外圈故障特征值较大而内圈故障特征值较小。13组轴承外圈故障数据正确识别率达84.6%，其中将轴承外圈故障误识别为正常轴承的比率为15.4%。

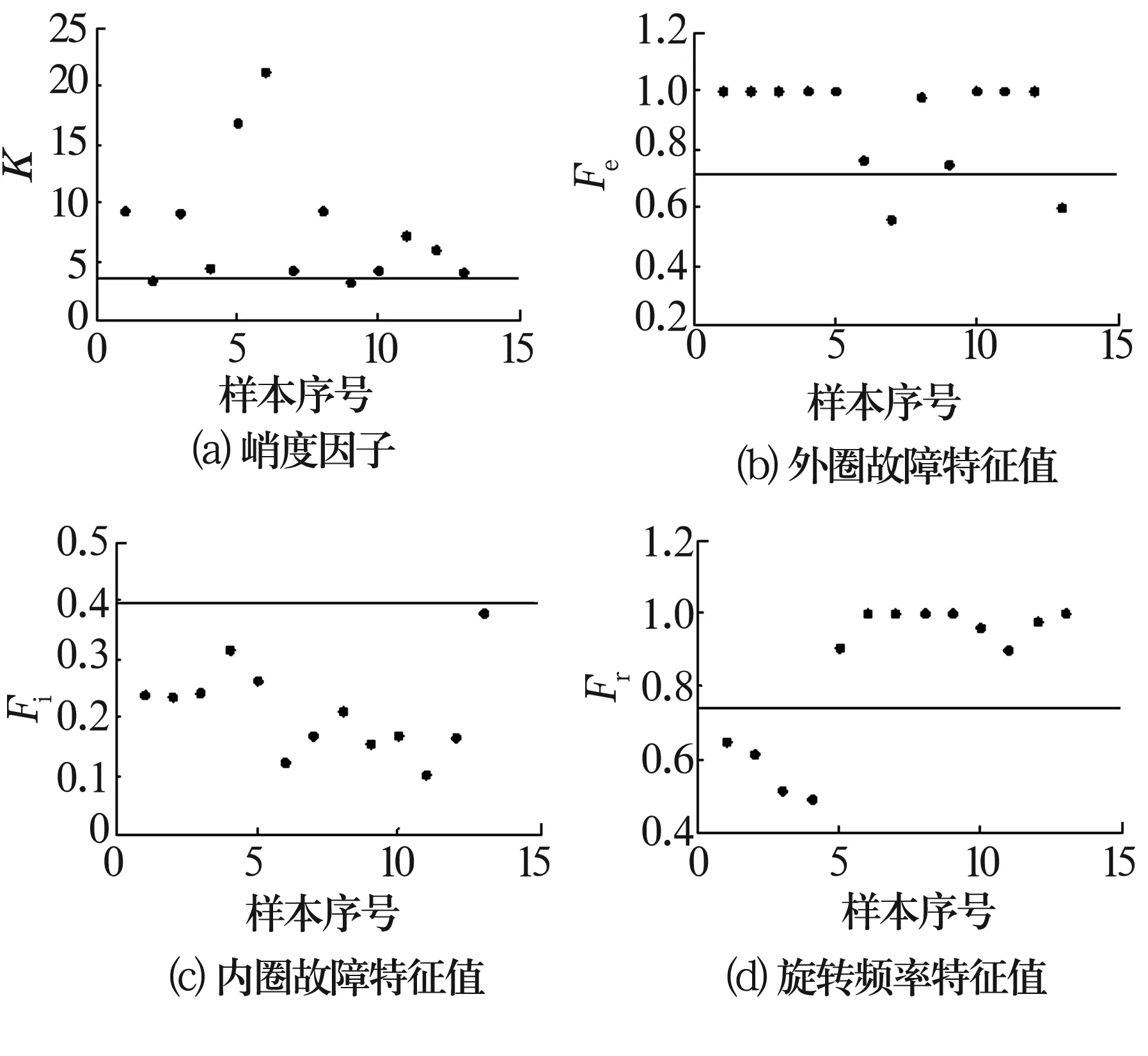
图4 外圈故障轴承测试结果

采集11组轴承内圈故障数据，同样应用上述方法，识别结果如图5所示。由5d可以看出，内圈故障的冲击作用受旋转频率调制。内圈故障数据的正确识别率达72.7%，其中将内圈故障误识别为外圈故障的比率为27.3%。内圈故障位置随旋转而不断变化，因此内圈故障通常难于诊断。

图5 内圈故障轴承测试结果

5 结束语

针对轴承故障诊断中存在故障样本不足，故障诊断知识获取困难的情况，提出的基于Weka平台的C4.5决策树的故障知识自动获取方法应用于实际的轴承故障数据，能够较好地对故障类型进行识别，充分说明了该方法在轴承故障诊断中的有效性和准确性。而且这种方法具有较强的推广性，可用于其他类型数据的知识获取。