航空发动机主轴高速圆柱滚子轴承保持架柔体动力学仿真

杨海生，邓四二，李晌，陈国定

(1.西北工业大学 机电学院，西安 710072；2.河南科技大学 机电工程学院，河南 洛阳 4710033.洛阳LYC轴承有限公司，河南 洛阳 471039)

航空发动机主轴用高速圆柱滚子轴承使用于高速、高温、轻载环境下，工作中保持架与多个滚子之间存在着摩擦、磨损和剧烈的碰撞，可能发生运动失稳或疲劳断裂,引起轴承早期失效，因此保持架的动态性能研究引起了许多学者的关注。文献[1-2]建立了轴承拟静力学分析模型并预测了保持架打滑率；文献[3]建立了动力学模型研究了滚子轴承保持架的不稳定性；文献[4]研究了套圈为柔性体的滚子轴承保持架的动力学特性，并分析了刚柔耦合产生的影响。文献[5-6]建立的轴承动力学模型可以计算滚动体载荷分布，动态模拟保持架的打滑。文献[7]对航空发动机主轴承中保持架的振动特性进行了分析。文献[8]建立了承受4自由度载荷的滚子轴承动力学模型，分析了工况参数和结构参数对高速滚子轴承动态特性的影响规律。文献[9]分析了保持架结构参数对轴承动态性能的影响。

从已有文献来看，大多数圆柱滚子轴承动力学分析模型都是将保持架整体视为刚性体，仅考虑接触区域的弹性变形；而另一部分文献虽然将保持架视为柔性体，但对保持架与滚子之间的作用力却做了简化假设。航空发动机高速圆柱滚子轴承保持架的梁较薄，保持架整体结构柔性不容忽视；而保持架与滚子之间作用力也与整个轴承工作情况相互耦合。文中将保持架作为柔性体，建立高速圆柱滚子轴承保持架动力学方程，利用ADAMS/SOLVER对方程进行积分求解，对航空发动机主轴高速圆柱滚子轴承保持架动态性能进行仿真。

1 保持架动力学分析模型

在高速圆柱滚子轴承内部各零件相互运动和作用关系基础上[10]，建立了轴承动力学分析模型，模型中考虑了保持架的柔性特性。

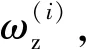
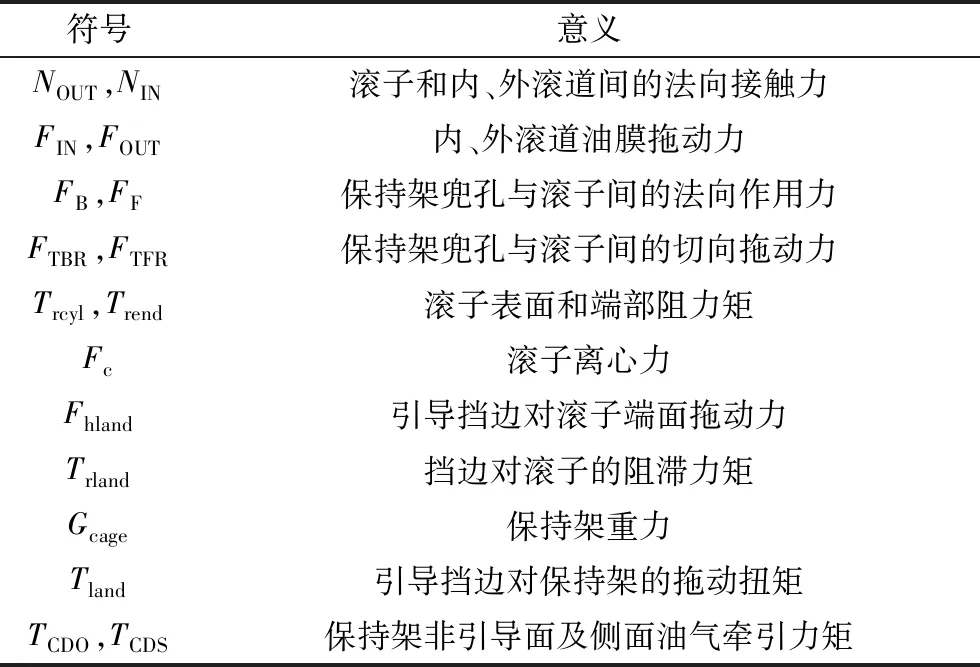
表1 作用力

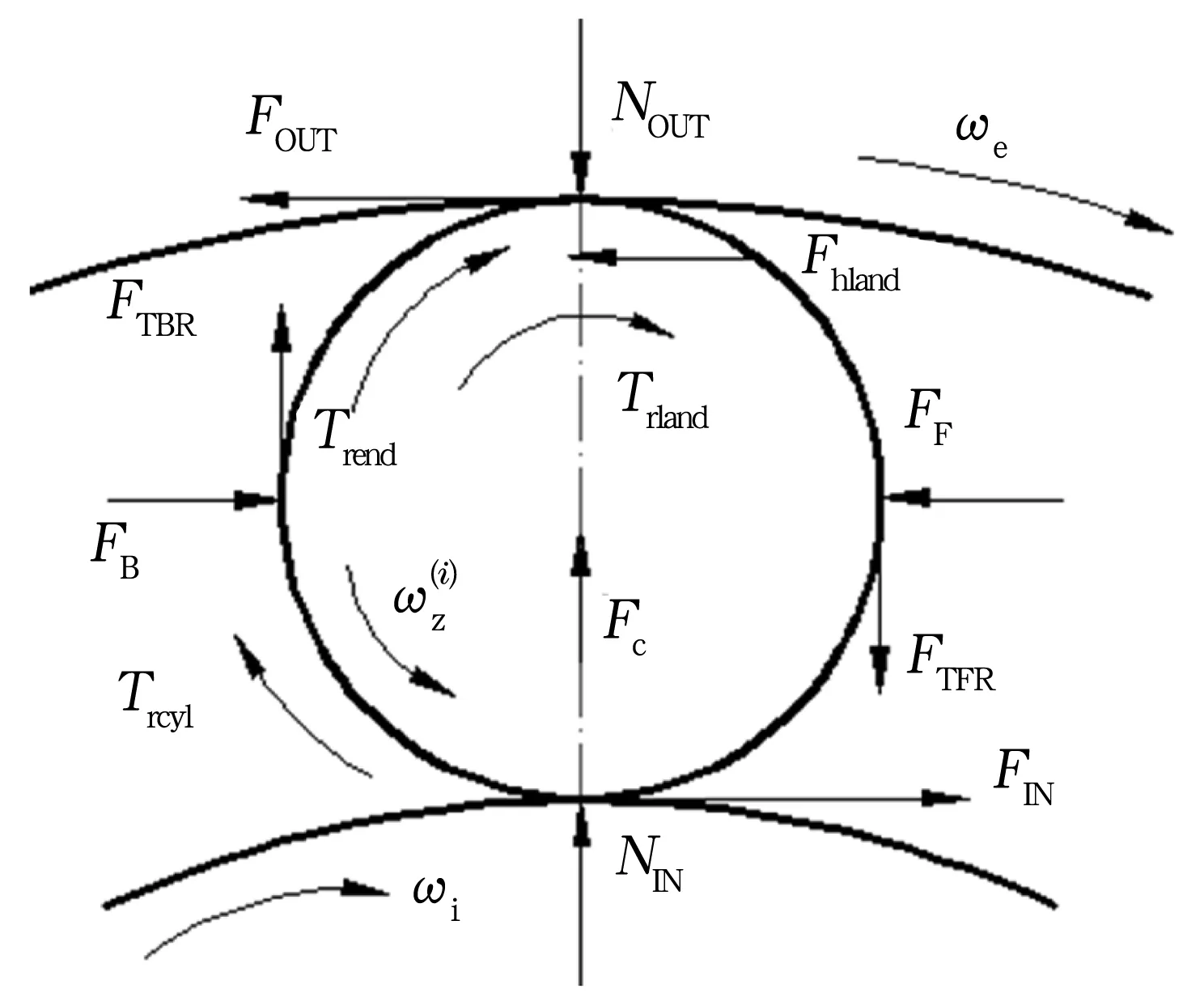
图1 滚子受力

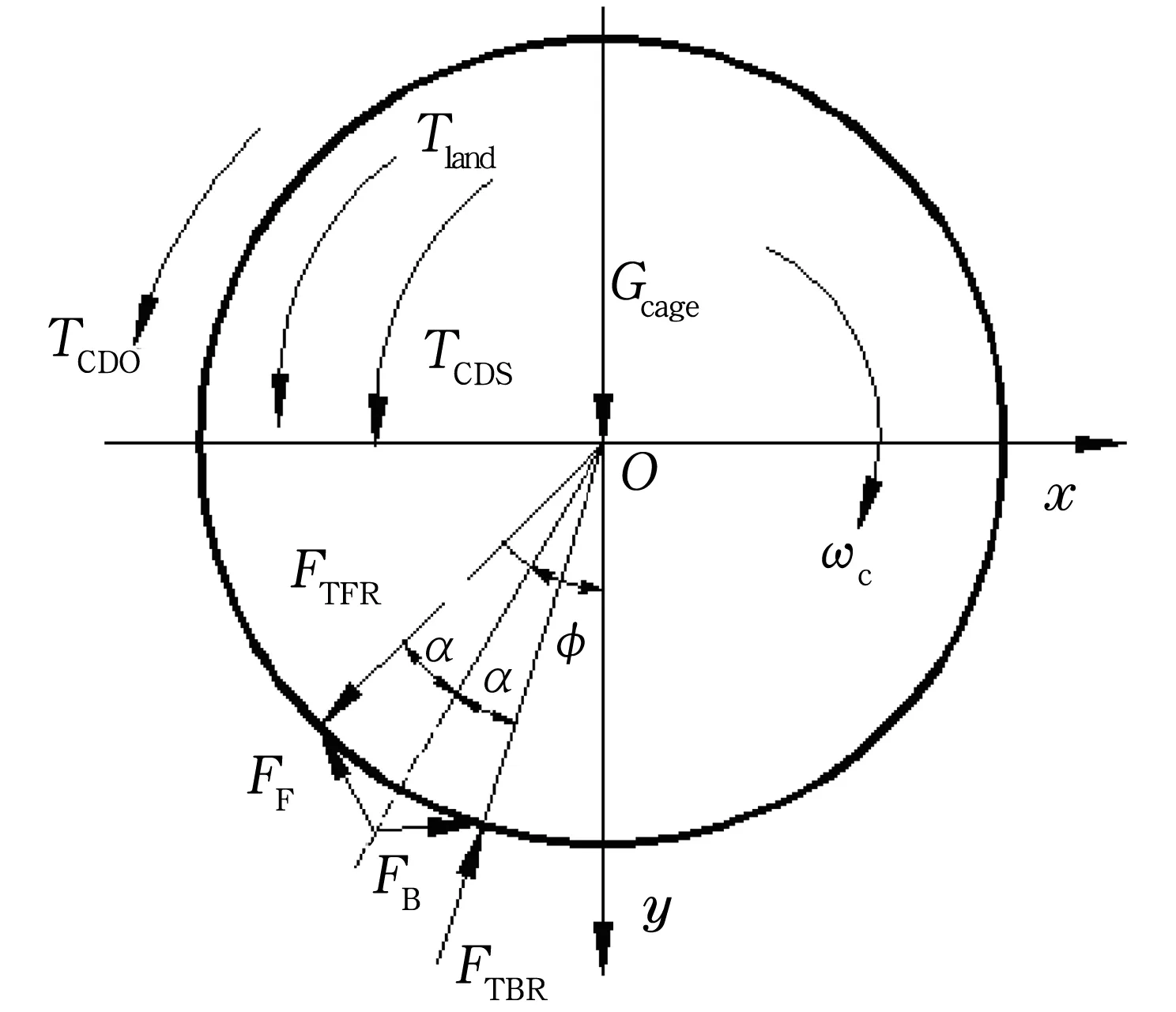
图2 保持架受力

根据滚子、保持架和套圈的受力情况，可建立高速圆柱滚子轴承动力学方程。

1.1 保持架运动方程

采用修正的Craig-Bampton子结构模态综合法[12-13]，通过Lagrange方程可得出圆柱滚子轴承保持架的柔体动力学方程

(1)

ζ=[RΩql]T，

Qc=[QtQrQm]T，

(2)

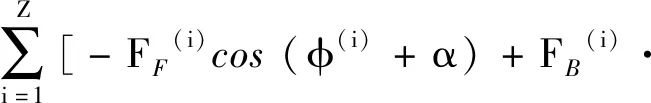
(3)

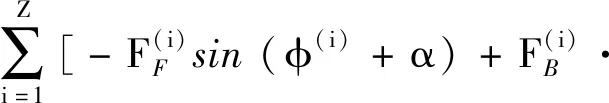
(4)

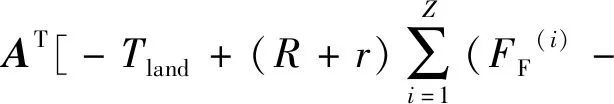
FB(i))-TCDS-TCDO]，

(5)

(6)

1.2 滚动体运动方程

(7)

Trland(i)-Trend(i)-Trcyl(i)，

(8)

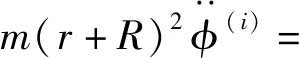
FB(i)-FF(i)+Fhland(i)]，

(9)

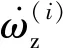
1.3 套圈平衡方程

(10)

(11)

式中：POx，POy为x和y方向上的外载荷；MOx，MOy为外力矩；MF(i)，MN(i)为接触区的摩擦力矩。

2 保持架动力学性能分析

采用Visual Fortran进行ADAMS/SOLVER用户自定义子程序开发，对每一瞬时圆柱滚子轴承零件位置、姿态、速度及角速度进行实时测量，并据此计算各作用力大小、方向。用户定义子程序经编译成为动态链接库(DLL)供ADAMS/SOLVER求解器调用，对 (1)～(11)式组成的圆柱滚子轴承刚柔多体动力学方程组进行求解，从而对圆柱滚子轴承保持架动力学特性进行分析。现针对某型号航空发动机主轴圆柱滚子轴承保持架进行动态性能分析，外圈转速ωe=12 000 r/min，内圈转速ωi=10 000 r/min，内、外圈同向转动，径向载荷2 000 N，保持架外圈引导，轴承及保持架主要参数见表2。

表2 轴承及保持架主要参数

2.1 保持架模态分析

文中计算了前26阶自由振动频率和模态，据此可以研究其共振、变形状态。从计算结果来看保持架的振动具有环类零件振动的特性。前6阶为刚性模态，系统自动忽略，表3列出了该保持架其余各阶固有频率。从数值上看该保持架的固有频率最小为538.78 Hz，因此低频段一般不会发生共振。

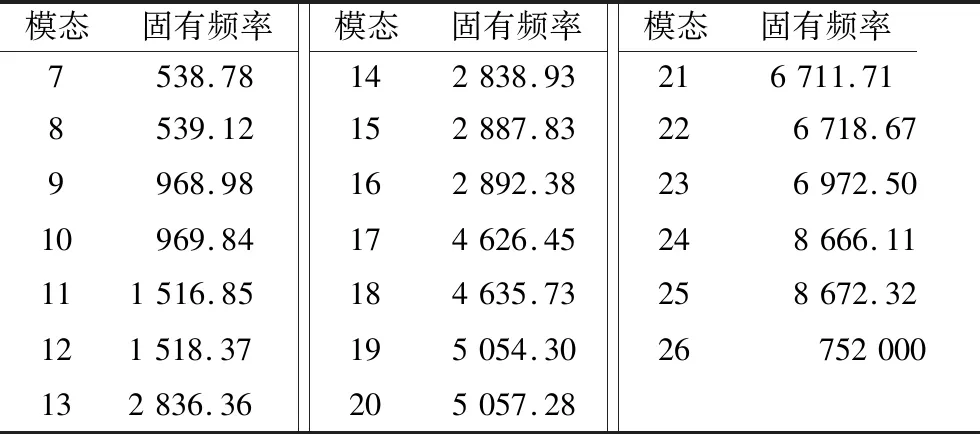
表3 保持架的固有频率 Hz

图3所示为该保持架几种典型振型。12阶、15阶模态分别为保持架在环平面内的弯曲振动，因保持架在环平面内的弯曲刚度较小，振动频率较低，工作中较易被激发；20阶模态为保持架在圆周方向上的弯扭耦合振动；24阶模态主要是保持架端面的整体倾斜，发生面外扭转。从振型分析可以看出，保持架振动时梁易产生较大的剪切应力，最大应力出现在梁的交汇处，因此疲劳裂纹最容易在此处发生，这与实际应用中保持架的失效形式较为一致。

图3 保持架振型

2.2 工况对保持架动态性能的影响

图4为不同径向载荷下保持架的打滑率。由图4可知：随着径向载荷的增加，保持架的打滑率呈减小趋势，这是由于径向力的增大会使滚子接触力增大，从而使滚子与套圈之间的拖动力增大，滚子和保持架的公转速度也随之增大，这与文献[14]中得到的结果相吻合。为避免保持架出现较大的打滑率，应控制最小径向载荷，文中所研究轴承的径向载荷为2 000 N时不会出现较大的打滑。

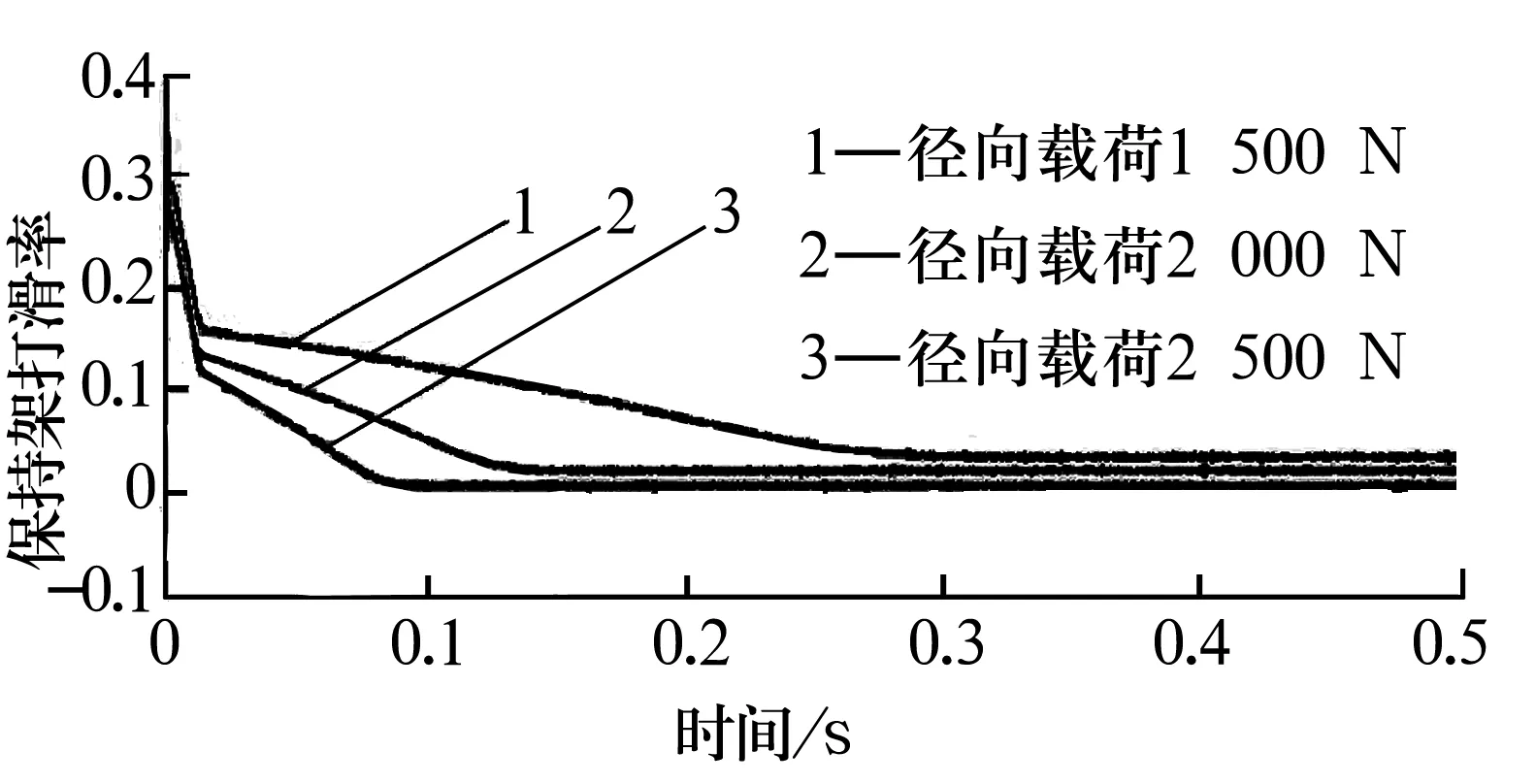
图4 不同径向载荷下保持架的打滑率

图5为轴承外圈转速不变，内圈转速对保持架打滑率的影响情况。由图5可知：随着内圈转速的增大，保持架打滑率呈增大趋势，达到稳态所需时间较长。这是由于内圈转速提高，滚子与内圈之间拖动力不足，导致保持架公转速度下降的缘故，这也说明高速轻载轴承打滑是个严重的问题。

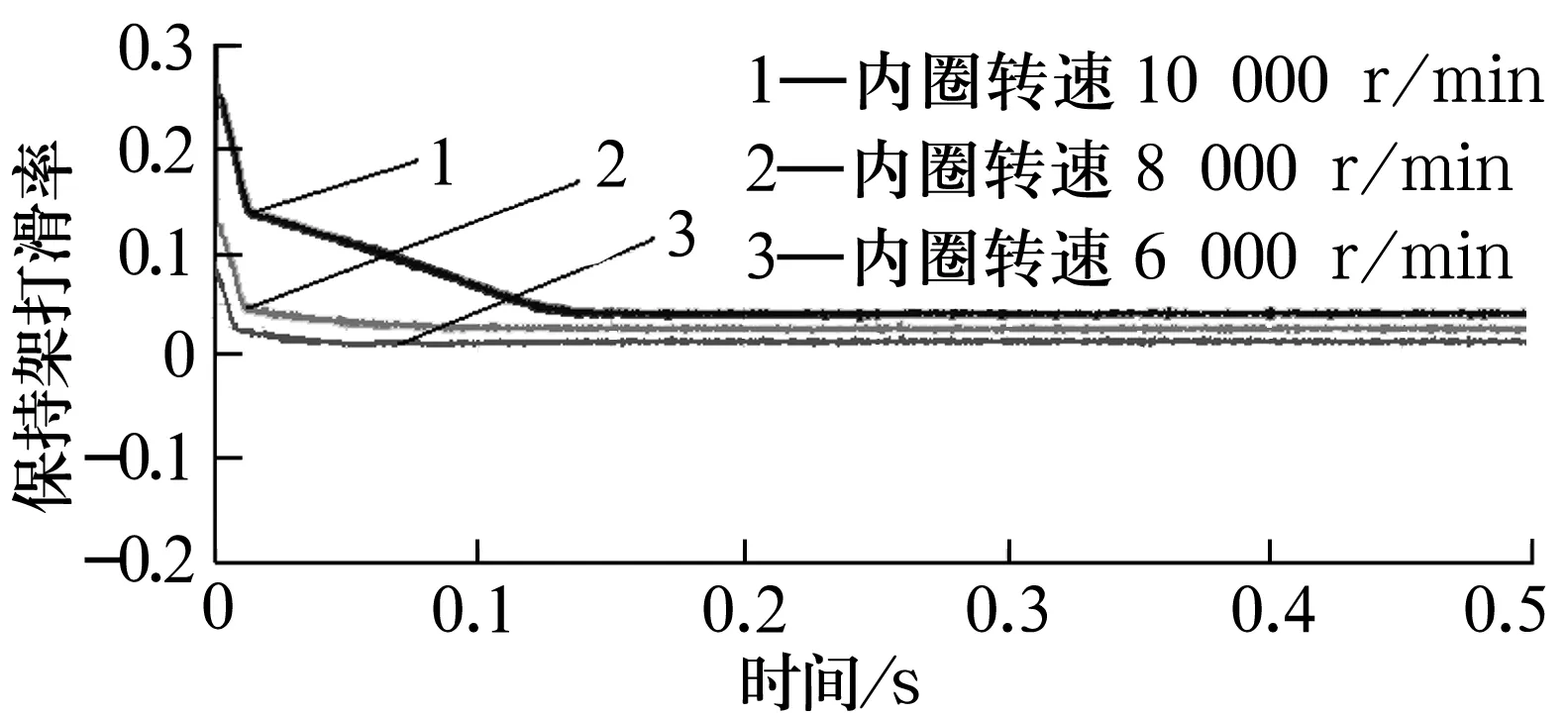
图5 不同转速下保持架的打滑率

2.3 结构参数对保持架动态性能的影响

图6为轴承径向游隙与保持架打滑率的关系曲线。由图6可知：在一定范围内，随着径向游隙的增大，保持架的打滑率呈减小趋势。这是由于径向游隙的增大，轴承的载荷分布范围减小，最大受载滚子与滚道之间法向接触力和切向拖动力增大，最终使保持架转速升高，因此高速轻载轴承应取较大的径向游隙值。然而过大的径向游隙会降低轴承的运动精度，在文中研究的实际工况中，径向游隙取值较为合理，不会产生较大的打滑。

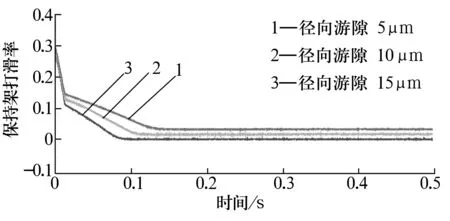
图6 不同径向游隙下保持架的打滑率

兜孔间隙与引导间隙对保持架工作特性有较大的影响，文中着重研究了两间隙的比值的影响情况。表4为不同间隙比下滚子与保持架兜孔之间最大作用力仿真结果。由表4可知，随着兜孔间隙与引导间隙比值C的增大，滚子与保持架兜孔之间最大作用力也随之增大，意味着滚子与保持架间的碰撞更加剧烈。仿真结果也显示出此时保持架运动具有较差的稳定性。工作中，在兼顾其他要求情况下应选择较小的C值，本文选C=0.5较为合适。

表4 不同C值时滚子与保持架兜孔间最大作用力 N

3 试验验证

采用我校航空轴承保持架性能试验装置进行试验验证。试验装置如图7所示，可进行保持架转速、位移的瞬态测量。以文中所述某型号航空发动机主轴圆柱滚子轴承为例，进行柔性保持架的打滑率计算，并与刚性保持架和试验数据进行对比。仿真计算保持架达到稳态后打滑率的均值如图8所示。与全刚体模型相比，刚柔耦合模型保持架的打滑率更接近试验值，证明了文中方法的可行性和程序的可靠性。

1—外圈轴；2—支点轴承；3—试验轴承；4—试验供油；5—径向加载活塞；6—加载轴承；7—内圈轴；8—测速杆

图8 径向载荷与保持架打滑率的关系

4 结论

(1) 保持架振形分析显示，在梁处易产生较大剪切应力，其最大值出现在梁的交汇处。

(2) 套圈转速的提高会引起保持架的打滑率增大，为避免保持架出现较大的打滑率，工作中应控制最小径向载荷。

(3) 径向游隙的增大能降低保持架的打滑率，但径向游隙过大同时会影响到轴承运动精度和使用寿命，应根据实际工况选择合适大小的游隙值，在文中研究算例中，径向游隙取值满足要求。

(4) 保持架的稳定性随着兜孔间隙和引导间隙的比值变大而变差，应在兼顾其他要求情况下选择较小的间隙比值。