基于三维光学测量系统的三维建模软件研究①

唐瑞林，吴 侃

（1.中国矿业大学环境与测绘学院，江苏 徐州221008；2.江苏省资源环境信息工程重点实验室，江苏 徐州221008）

0 引 言

随着人们对复杂曲面物体的建模需要，三维光学测量建模技术以其独有的优势获得了迅猛的发展，它既有摄影测量的高效率，又有光栅测量的良好精度，并采用非接触的测量方法，直接得到真实物体表面的采样点，利用点云数据重构出任意曲面。这种方法不受曲面复杂度影响，可以达到很高的重构精度。目前广泛应用在汽车工业、航空航天工业、船舶工业、建筑工业等，通过三维坐标测量可以完成质量检测、变形测量、逆向工程等。某些特殊场合，三维扫描仪还具有独特的、不可替代的作用。

以西安交通大学研发的三维光学测量系统为工具，采集风扇模型的表面点云，构建其三维模型，摸索出三维扫描建模的流程，积累建模经验，并研究点云数据处理中的关键技术，为三维光学扫描领域软硬件开发提供经验。

1 系统简介

该工业测量系统由以下两部分组成：XJTUDP三维光学摄影测量系统和XJTUOM三维光学面扫描系统［1]，如图1和图2所示。

XJTUDP系统是工业非接触式的光学三坐标测量系统，也称为数字工业近景摄影测量系统，可以精确地获得离散的目标点三维坐标，是一种便携式、移动式的三坐标光学测量系统，可以用于静态工件的质量控制和静态变形分析实时测量。

XJTUOM三维光学面扫描系统是一个三维实体数字化系统，采用国际最先进的外差式多频相移三维光学测量技术。其测量原理是由光栅投影装置投影多幅多频光栅到待测物体上，成一定夹角的两个摄像头同步采集相应图像，对图像进行解码和相位计算，解算出两个摄像机公共视区内像素点的三维坐标。

在利用点云数据进行三维建模的过程中，数据采集是很重要的一个环节，它直接关系到最后创建出的三维模型质量。采集过程中，需要针对将来的应用需求设置合适的点云采集密度，以及如何设置合理的视点，在复杂的工程环境中，避免过多的周围物体对目标物体产生的遮挡等影响。同时可以采集纹理影像数据，作为几何信息的补充。具体的流程有：前期准备工作、粗扫、精扫控制点、精扫目标区域、拍摄纹理照片等。

2 基于点云数据的三维建模的理论和方法

若按曲面表示形式分类，目前曲面重构算法大致可分为三种：网格类方法、参数类方法和隐式类方法［2－5]。重点介绍不规则三角形生长法构建TIN的方法。

Brassel和Reif于1979年提出了该算法，主要思路是先找出点集中相距最短的两点连接成为一条Delaunay边，按Delaunay三角网的判别法则找出包含此边的Delannay三角形的另一个端点，依次处理所有新生成的边，直至所有的边找不到能形成合理Delaunay三角形的端点。三角网生长算法的基本步骤是：

1）以任一点为起始点；

2）找出与起始点最近的数据点相互连接形成Delaunay三角形的一条边作为基线，按Delaunay三角网的判别法则（即它的两个基本性质），找出与基线构成Delaunay三角形的第三点；

3）基线的两个端点与第三点相连，成为新的基线，迭代以上两步直至所有基线都被处理。如图3所示。

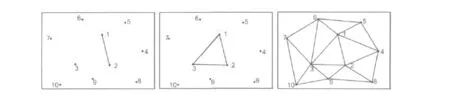
图3 不规则三角形生长法构TIN［6]

3 三维建模程序开发

1）系统结构

系统主要分构建TIN模型和模型的三维显示两个部分。主要功能模块如图4所示。

2）数据管理

数据管理主要是存储点云数据点（point）信息、各条基线（line）信息以及构网的三角形（Triagle）信息［7]。

3）构建TIN模型

建模程序开发重点在于能够生成点云数据的TIN模型［7]，经过研究分析，设计出其算法流程如图5所示。

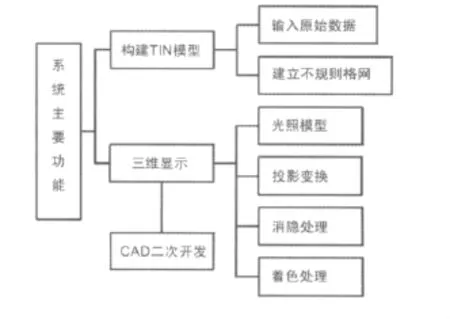
图4 系统功能模块结构图

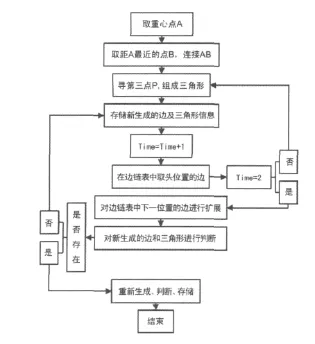
图5 三角形生长法构建TIN结构图

4）三维显示

利用CAD的二次开发［8]将构好的TIN模型显示出来，重现出点云数据的三维形态，给人以直观感受。方便人们对其进行建模精度评判并加以利用。在模型三维显示算法中，需要对前面的TIN模型进行光照模型、投影变换、消隐处理及着色处理。

①投影变换

建立透视投影模型，确定视点、投影面等相关参数，根据投影变换公式计算三角划分后的三角面在投影面上的坐标，如图6所示。

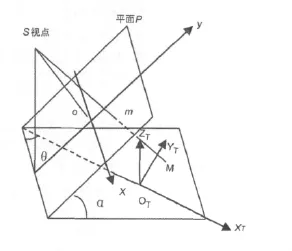
图6 投影变换图

图中，任意一点M在坐标系OT－XTYTZT中的坐标为（XM，YM，ZM），它在投影平面P上的像点为m，则m点在投影坐标系O－xy中的坐标（xm，ym）可由公式（1）求出。

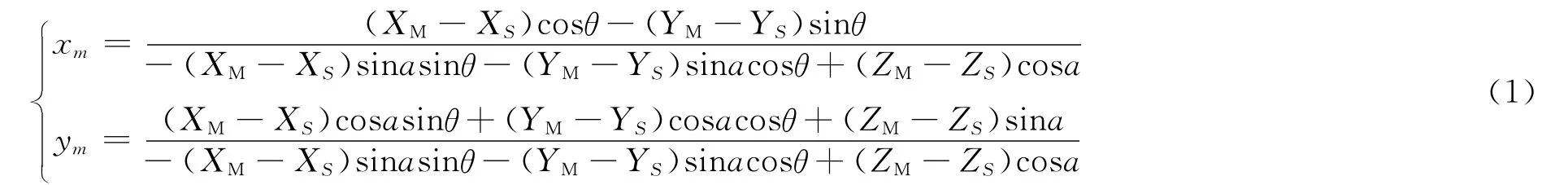
②消隐处理

按照画家算法进行图形的消隐显示，其主要思想是：首先把屏幕显示成背景颜色；把各个三角形面按照距视点的远近距离进行排序，把最远的放在前面；从表头到表尾逐个取出面素投影到屏幕上。

4 实 例

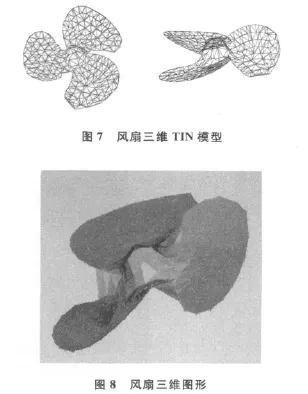
利用三维光学面扫描得到的风扇的点云数据，将其导入设计的建模程序，得到点云数据的TIN模型，如图7所示。将构建好的TIN模型进行三维显示，得到风扇的三维模型如图8所示。由图可以看出，所设计的程序能够很好的反映不规则物体的三维形态，建模精度比较高。

5 结 论

基于三角形生长法构建散乱点云的TIN模型，具有简单易实现、算法效率高的特点，算法只需要散乱点云，无须其他信息（法矢量、拓扑信息等），算法不但可以处理小物件的点云数据，还可以分块实现大物件的点云数据建模。在处理不连续点云时加入了阈值，成功地避免了不连续点云之间的相互影响。并利用AutoCAD二次开发实现模型的三维显示。

考虑到实际的散乱点云有时特别复杂，本程序结构简单，功能并不完善，导致构网曲面光滑程度不高，构网速度有待提高，不适应于很高密度点云数据进行建模。下一步的工作将在算法中增加人工干预的成分以便处理特别复杂的散乱点云的三角网格重构，也需要研究构造好的网格的特征信息识别算法。

［1]西安交通大学模具与塑性加工研究所，西安交通大学信息机电研究所.西安交通大学三维光学测量技术［R].西安：西安交通大学，2008：20－23.

［2]葛金辉.曲面重构算法的发展现状述析［J].通化师范学院学报，2003，24（2）：33－36.

［3]JANK，G Z.Point cloud surfaces using geometric Proximity graphs［J].Computers＆Graphics，2004（28）：839－850.

［4]朱东波，张舜德，李涤尘，等.密集散乱测量数据点的B样条曲面拟合研究［J]..计算机辅助设计与图形学学报，2001，13（12）：1123－1128.

［5]Muraki S.Volumetric shape description of range data using"Blobby Model"［C]∥ Computer Graphics Proceedings，Annual Conference Series，ACM SIGGRAPH，Los Angeles，California，1991：227－235.

［6]杜培军，程朋根.计算机地图制图原理与方法［M].徐州：中国矿业大学，2006：101－102.

［7]江剑霞，刘少华，严汉英.VB环境下不规则三角网的算法设计与实现［J].四川测绘，2006，29（2）：64－67.

［8]杨新林，冯冠辉，钱建国.三维激光扫描仪点云数据在AutoCAD中的处理方法研究［J].陕西煤炭，2008，（3）：37－38.