GPS模块数据分析与处理①
陈 赛,李建朝
(河南科技大学机电工程学院,河南 洛阳471003)
0 引 言
全球定位系统(GPS)的出现与发展,为人类的导航和定位提供了可靠的保障。随着社会的进步和科学技术的发展,GPS定位技术已经越来越接近普通人的生活。GPS模块的出现,使GPS为普通民众所用成为可能。GPS模块拥有体积小、重量轻、功耗低、携带方便,价格低廉等优点,但是GPS模块定位精度到底如何呢?能否为导航和定位提供有用的数据?基于一款GS-15CGPS模块,对所采集的数据进行分析和处理,对误差源进行了分析,给出了相应的试验方法和结果。
1 GPS数据的采集和计算
1.1 几个基本概念和公式[1]
1.1.1 算术平均值
在系列测量中,被测量的n个测得值的代数和除以n而得出的值称为算术平均值。设l1,l2,…,ln为n次测量所得值,故算术平均值¯l为:

1.1.2 测量的标准差
由于随机误差的存在,等精度测量列中各个测量值一般皆不相同,它们围绕着该测量列的算术平均值有一定的分散,此分散度说明了测量列中单次测量值得不可靠性,必须用一个数值作为其不可靠性的评定标准。单次测量的标准差σ是表征同一被测量的n次测量值的测得值分散性的参数,可作为测量列中单次测量不可靠性的评定标准。
由贝塞尔(Bessel)公式

其中,vi为残余误差,残余误差为测得值与算术平均值之差,即

1.1.3 单次测量的极限误差
测量的极限误差是极端误差,测量结果(单次测量或测量列的算术平均值)不超过该极端误差的概率为P,并使差值(1-P)可予忽略。设极限误差为δlim,则有公式

其中,t为置信系数,当t=3时,对应的概率P=99.73% .
1.2 数据的采集和计算
表1是GPS模块开机稳定后的数据,共记录了20次,主要记录了经度和纬度值。

表1 开机稳定后的数据(单位:′)
1.2.1 所测数据的准确性判断
表1是GPS模块测得的数据,但是这些数据是否准确?能否反映出正确的地理位置[2]。将GPS模块输出信号接入灵图9导航地图,(注意:GPS模块的位置与采集数据的位置是同一个位置),则在地图上出现如图1所示,画面中所在地即为定位位置。由灵图9地图可知,定位后的位置基本上能够反映模块所在位置,所以表1所测数据是比较准确的定位数据。

图1
1.2.2 数据的计算
设测量的20个经度值分别为x1,x2,…,x20,求经度算术平均值x
由表1测得的数据,带入公式(1)可以算出:x=112°21.9628
同理,设测量的20个纬度值分别为y1,y2,…,y20,求纬度算术平均值y
由表1测得的数据,带入公式(1)可以算出:y=34°39.7222
将表1数据带入公式(1)(2)(3),可以算出
σx=0.0082 σy=0.0104
由公式(4),可以算出,经度和纬度的极限误差分别为
δlimx=±3×σx=±0.0246
δlimy=±3×σy=±0.0312
2 经纬度定义及与实际里程数据换算[3]
2.1 经度
经度泛指球面坐标系的纵坐标。定义为地球面上一点与两极的连线与0°经线所在平面的夹角。国际上规定,把通过英国首都伦敦格林尼治天文台原址的那一条经线定为0°经线,也叫本初子午线。从0°经线算起,向东、向西各分作180°,以东的180°属于东经,习惯上用“E”作代号,以西的180°属于西经,习惯上用“W”作代号。东经180°和西经的180°重合在一条经线上,那就是180°经线。在地图上判读经度时应注意:从西向东,经度的度数由小到大为东经度;从西向东,经度的度数由大到小,为西经度;除0°和180°经线外,其余经线都能准确区分是东经度还是西经度。经度的每一度被分为60角分,每一分被分为60s.一个经度因此一般看上去是这样的:东经23°27′30"或西经23°27′30".更精确的经度位置中秒被表示为分的小数,比如:东经23°27.500′,但也有使用度和它的小数的:东经23.45833°.
2.2 纬度
纬度是指某点与地球球心的连线和地球赤道面所形成的线面角,其数值在0至90°之间。位于赤道以北的点的纬度叫北纬,记为N,位于赤道以南的点的纬度称南纬,记为S。赤道定为纬度零度,向南向北各为90°,北极就是北纬90°,南极就是南纬90°.同样,纬度的每一度被分为60角分,每一分被分为60s.一个纬度因此一般看上去是这样的:南纬23°27′30"或北纬23°27′30" .更精确的纬度位置中秒被表示为分的小数,比如:南纬23°27.500′,但也有使用度和它的小数的:北纬23.458 33°.
2.3 经纬度与实际里程的数据换算
地球的子午线总长度大约40008km.
平均:纬度1°大约111km;纬度1′大约1.85km 纬度1″大约30.9m.
但经度的每个度的距离从0km到111km不等。它的距离随纬度的不同而变化,等于111km乘纬度的余弦。比如,洛阳地区在北纬34°左右,所以在洛阳地区平均值:经度1°大约92km;经度1′大约1.53km;经度1″大约25.6m.
3 GPS模块实测数据的里程误差
3.1 GPS模块输出数据在理论上的误差
本GPS模块输出经纬度数据的格式为度分格式,即×××度××××××分,比如东经23°27.5000′.由测量数据可知,所测量数据的最低位为0.0001′,即为0.006″,故由上述换算关系,如果在洛阳地区,经度的最小里程测量精度为0.15m,纬度的最小里程测量精度为0.19m.故在理论上,GPS模块的测量精度是很高的,可以达到厘米级。
3.2 GPS模块的实际测量误差
由前面的计算和分析可知,GPS模块开机经度和纬度的极限误差分别为
δlimx=±3×σx=±0.0246′=±1.48″;
δlimy=±3×σy=±0.0312′=±1.87″
换算为里程误差则为
llimx=±37.9m;llimy=±57.8m
这一数据说明,当GPS模块刚刚开机时,如图2所示,如果用户在原点,根据开机后的数据,则矩形区域内的任一点都有可能是用户所在的位置[4]。这相当于定位稳定后的定位精度大概为足球场大小。这一定位精度并不算高。
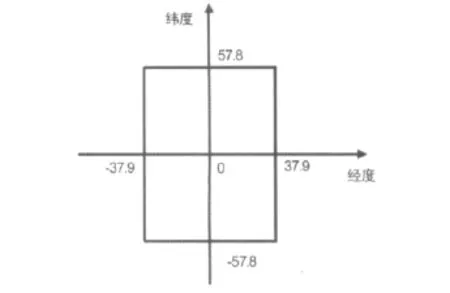
图2 误差区域
3.3 GPS模块定位稳定后的误差分析[5]
表2数据是GPS模块定位稳定后采集的数据,数据采集地点和表1数据采集地点相同。数据采集形式为:开机半小时后开始采集数据,数据采集间隔为10min一次,共采集了六次数据。
由表2数据可知:

表2 GPS模块定位稳定后采集的数据(单位:′)
1)由表1数据算出来的经纬度算术平均值还是比较准确的,此算术平均值与真值比较接近了。
2)GPS模块定位稳定后数据波动较小,而且精度已经较高。
如果把由表1数据算出来的经纬度算术平均值作为真值,从表2数据可以看出,第六组数据误差最大,则vxi=vx6=-0.008 8′,vyi=vy6=0.006 1′,换算为实际里程为lx=-13.5m,ly=11.3m.
也就是说,当出现的误差最大时,定位区域为一个半径大约为13m的圆。如果作为民用的导航设备,这一误差是完全可以接受的,并且可以认为,这一定位精度已经比较高了。
4 GPS模块测量值的误差分析
4.1 关于GPS测量的误差来源与分类[6]
GPS误差来源与分类见表3

表3 误差来源与分类
4.2 单点定位[7]
采用单个GPS接收机独立确定待测点在协议地球坐标系中的绝对位置的方法称为单点定位或绝对定位。目前GPS系统采用的坐标系统为WGS-84系统,所以,单点定位的结果是接收机在WGS-84系统的坐标值。单点定位的优点是,只需一台GPS接收机即可实现独立定位,野外作业的实施较为方便,数据处理也比较简单。但是单点定位受GPS卫星星历误差和大气延迟误差的影响较为严重,所以定位精度一般。
本测量属于单点定位。
4.3 误差分析
由上述分析可知。本测量的测量误差主要分为卫星星历误差和大气延迟误差[8],现在就这两种误差进行分析。
4.3.1 卫星星历误差分析
由广播星历参数或其他轨道信息所给出的卫星位置与卫星的实际位置之差称为星历误差。广播星历是卫星导航电文中所携带的卫星空间位置信息。它是根据美国GPS控制中心跟踪站的观测数据进行外推预算,由地面注入站发送给GPS卫星,再通过GPS卫星向地面发播的一种预报星历。由于卫星在运行中受到多种摄动力的影响,目前单靠地面监测站尚不能精确可靠的测定作用在卫星上的各种摄动力因素的大小及变化规律,所以预报数据中存在着较大的误差。
在GPS单点定位中,卫星被作为空间的已知点,卫星星历被作为已知的起算数据。这样,星历误差必将以某种方式传递给测站坐标,从而产生定位误差。在GPS绝对定位中,广播星历误差对测站坐标的影响可达几十米。
为了尽可能消弱星历误差对定位的影响,一般采用同步观测求差法或轨道改进法。显然,卫星星历误差对相距不太远的两个测点的定位影响大致相同,故可采用两个或多个近距离的观测点对同一颗卫星进行同步观测,求差,就可以消弱卫星轨道误差的影响。这种方法就是同步观测求差法。另外,轨道改进法的基本思路是:在数据处理中,引入表述卫星轨道偏差的改正数,并假设在短时间里这些改正参数为常量,将其作为待求量与其他未知参数一并求解,从而校正卫星误差。
4.3.2 大气延迟误差分析
4.3.2.1 电离层折射误差分析
由于地球周围的电离层对电磁波的折射效应,使得GPS信号的传播速度发生变化,从而导致卫星至接收机间的几何距离偏差。
对于电离层折射的影响,可以通过以下解决途径削弱。
1)利用电离层模型加以改正;
在导航电文中提供电离层改正模型,该模型一般用于单频接收机,用目前所提供的模型可将电离层延迟影响减少75%
2)利用双频观测减少电离层延迟;
3)利用两个观测站同步观测量求差;4)选择有利观测时段。
4.3.2.2 对流层折射误差分析
由于地球周围的对流层对电磁波的折射效应,使得GPS信号的传播速度发生变化,这种变化称为对流层延迟。从而导致卫星至接收机间的几何距离偏差。这种偏差叫对流层折射误差。
减弱对流层折射对电磁波延迟影响主要措施有:
1)利用对流层模型加以改正:实测地区气象资料利用模型改正,能减少对流层对电磁波延迟达92%~93% 。
2)利用同步观测量求差。
5 结 论
研究了GS-15C模块所测数据的可靠性,并对产生的误差进行了分析。基于以上的分析,GS-15CGPS模块所测得数据的误差在允许的误差范围内,属于正常的误差。故利用GS-15C模块去开发便携式GPS导航仪是完全可行的。
[1]费业泰.误差理论与数据处理[M].北京:机械工业出版社,2008:10-15.
[2]关桂霞,朱 虹,关 永.GPS定位误差分析与状态估计[J].计算机工程,2008.34(1);236-237.
[3]王惠南.GPS导航原理与应用[M].北京:科学出版社,2005:107-116.
[4]徐 琨.贺最嚯.冈茂德.全球定位系统动态定位误差分析与建模[J].西安电子科技大学学报·自然科学版.2008,35(4):749-753.
[5]胡 辉.高动态数字化GPS接收机的研制[D].上海:上海航天局,2002.
[6]RENATO F,TOMISLAV K M.GPS ionospheric error correction models[C]//The 48th Internation Symposium ELMAR-2006,Croatia.2006:215-217.
[7]BAO-YENT J.GPS软件接收机基础[M].北京:电子工业出版社.2008.
[8]许绍铨,张华海,杨志强,等.测量原理及应用[M].武汉大学出版社,2002:84-98.

