欧洲股票市场的规模和动因：基于不同β系数的资本资产定价模型实证研究

杨国莉 杨淑君 刘丽敏 武宗志

一、引 言

许多实证研究发现，小市值股票平均收益比大市值的更高（Reinganum，1981），该溢价与1月份季节性相连（Keim，1983；Ritter和 Chopra，1989）。最近研究结果证实国际市场也存在规模溢价（Clare等，1997；Heston等，1995，12个欧洲）。规模不是唯一与平均收益有关的公司特征，还与公司其它特征有关，如账面-市场价值、杠杆作用、盈利；然而，Fama和French（1992）表明，规模和账面-市场价值两者结合的股票似乎弱化了公司其他特征的作用。这些研究结果与有效市场假说和资本资产定价模型（CAPM）背离，常被称为“市场异常”。

最近的研究质疑小公司溢价异常现象的存在性。例如，Jegadeesh和 Titman（2001）；Dimson and Marsh（1999）；Knez and Ready（1997）。Wang（2000）检验了Compustat和CRSP数据，认为规模效应很大程度上是偏见造成的虚假统计推论，而不是资产定价异常。动因效应表现的更强烈，虽然Bekaert等人（1997）在新兴资本市场发现相反证据，Liew和Vassalou（2000年）的统计报告显示，日本和意大利存在非重大动因收益。对于这两种效应，有证据表明其周期性与经济状况有关，例如，Chordia和Shivakumar（2002）；Kim和 Burnie（2002）。

文献中的证据表明，近年小公司溢价已经在很大程度上消失，而动因效应可能不会在所有市场都重大。此外，有证据表明，这两种效应都与经济周期有关，因此，其重要性可能会随时间而变化。这些成果已获得主流国际资本市场的验证，而文献往往忽视较小资本市场。为此，本文旨在解决不同规模、不同重要性、不同交易系统、不同流动性和市场微观结构的13个欧洲市场样本的规模和动因效应等方面的问题。

第一，对规模和动因组合的盈利能力进行检验。我们发现，SMB套利组合（SMB）月均收益率的均值介于德国-0.03%到希腊1%之间，并且13个市场中只有2个市场具有统计显著性，而WML套利组合（WML）月均收益率的均值介于西班牙的0.37%和希腊的1.37%之间，且有8个市场具有统计显著性。

第二，我们检验次数及随着时间推移规模和动因组合盈利能力的一致性。以往的许多研究常以长期均值或不同子样本得出结论，而忽视了“异常”收益率的相对次数问题。这问题很重要，正如本文结果所示，这些效应随着时间推移发生的频率很低。我们表明，欧洲套利的规模和动因组合的正收益率，可能是由于其收益率大且重要的样本年份极少造成的。如，法国的WML组合，在整个样本期间存在统计上重大异常收益。年报表明，WML的异常收益率19年中只有4年在统计上是显著的；德国WML的异常收益率在19年中有3年显著，希腊仅有1年等。

第三，本文利用时间序列法，观测这些效应在静态和时间变化两方面是否与CAPM模型一致。如，规模和动因组合的最初研究中，这些效应与CAPM不一致，理由是该静态模型产生的β系数无法解释组合收益。然而，有关时变风险溢价的研究文献在不断出现（Ang and Chen，2007；Adrian and Franzoni，2008）。其中一些文献对早期研究结果提起质疑。本文研究结果显示，在大约一半的样本市场上规模和动因套利组合的收益与静态CAPM一致，然而，使用的方法考虑时间变化这个非系统风险时，在整个样本市场套利组合的收益与CAPM模型一致。

第四，我们旨在研究：小公司组合、大公司组合、SMB组合、盈利组合、亏损组合和WML组合的时变系统风险是否与经济周期有关。我们对每个组合和每个市场的β系数历史值进行时间序列回归，并试图找到与经济相关的系统风险假设一致的证据，因此可能会出现重要时间变化。本文的研究结果证实：以往之所以出现低小公司溢价和高动因溢价的研究结果是由于极少数样本年度存在巨大收益造成的。

二、数据和研究方法

资料来源于Datastream，含13个欧洲市场（奥地利，丹麦，法国，德国，希腊，爱尔兰，意大利，荷兰，挪威，西班牙，瑞典，瑞士和英国）的上市证券以当地货币折算的月末价格。DataStream数据的主要问题是误差，为提高数据集的质量并纠正可能出现的问题，使用Ince和Porter提出的4个筛选条件：（1）剔除所有未在参照国证券交易所上市的股票；（2）剔除非普通股股票；（3）剔除退市的零收益股票；（4）剔除下月逆转收益极高的股票。除希腊外所有市场的样本数据从1991年1月始到2009年12月止，希腊样本数据始于1992年1月。表1列出了样本年度每个市场所提供股票的平均数。

决定盈利组合和亏损组合的排名期为6个月，不含最近一个月。持有期也是6个月。假定每月我们拥有同比例的过去6个月形成的6个组合。盈利和亏损组合由最高和最低各占股票收益20%的股票组成。为了测量规模效应，我们使用Fama和French（1993）的方法。每年，基于样本中位数规模将样本分成两组，并对两种组合进行重新平衡。排位第一的是使用1990年12月到年底的市值，因此，从1992年对组合收益率样本按规模排序。所有组合都进行加权平均计算。

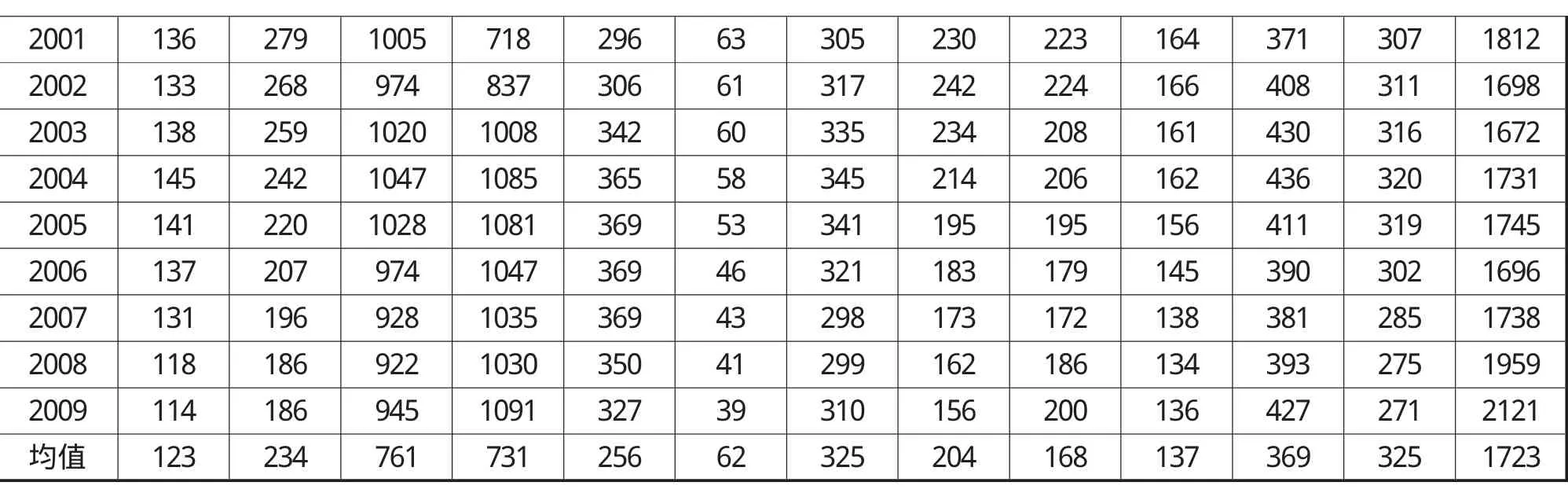
此表列出13个欧洲市场小市值股票组合的月均收益率（乘100倍）。“平均”所在行表示整个样本期的月均收益率。末行表示在我们样本期间的小市值股票组合的平均市值。为使数字具有可比性，所有市值都用百万欧元表示。对于非欧元国家，我们利用2008年末的汇率将平均市值进行折算。*表示在5%的水平上显著。

表1 每个国家每年投资组合中适宜证券的数量

2001 136 718 296 63 305 230 223 164 371 307 1812 2002 133 837 306 61 317 242 224 166 408 311 1698 2003 138 1008 342 60 335 234 208 161 430 316 1672 2004 145 1085 365 58 345 214 206 162 436 320 1731 2005 141 1081 369 53 341 195 195 156 411 319 1745 279 268 259 242 220 2006 137 1047 369 46 321 183 179 145 390 302 1696 2007 131 1035 369 43 298 173 172 138 381 285 1738 2008 118 1030 350 41 299 162 186 134 393 275 1959 2009 114 1091 327 39 310 156 200 136 427 271 2121 207 196 186 186均值 123234 1005 974 1020 1047 1028 974 928 922 945 761731 25662 325 369 325 204 168 1371723

表2 小公司股票组合月均收益率

此表列出13个欧洲市场大市值股票组合每年的月均收益（乘100）。“平均”所在行表示整个样本期间月均收益。末行表示在我们的样本期间大型股票的平均市值。为使数字具有可比性，所有市场价值用百万欧元表示。非欧元国家，我们利用2008年末的市场汇率将平均市值进行转化。*表示5%的显著性水平。

阿东当夜即往回赶。到家时，已近半夜。推门进屋，家里正一片狼藉。阿里被一根绳子捆着，蹲在墙角。医生给他打了安定，他垂着头，似乎已经睡着。他的脸上手上脏兮兮的，就像人们常见的流浪街头的疯子。阿东立即泪如泉涌。他大声吼道：“哪个混账捆的!爸爸你太过分了，爸爸你怎么能这样对他!”

表3 大公司股票组合的月均收益率

1996 2.442.72*4.26*1997 –0.40 0.32 –0.60 0.34 0.62 0.35 0.42 –0.38 1.15 –0.21 –0.14 2.84*0.71 4.08*2.53 5.42*4.18*3.37*5.97*3.84*2.80*1998 –1.27 –0.16 0.43 1.70* –0.98 0.80 1.30 0.64 0.86 0.75 1.26 1999 0.41 0.44–1.10 2.06*0.58 2.76*2.42*2.60*3.13*1.03 1.20 2000 1.35 1.75 3.76 3.67*3.71*2.15 2.46*3.21*1.98*2.90*0.77 2001 1.25 2.51 6.93 0.73 4.00 0.67 –2.41 3.07 –0.20 1.48 –0.31 2002 0.63 1.36 14.97*1.31 1.75 1.60 4.02*–0.61 3.43*2.18*3.28*2003 0.17 –0.40–7.40*1.62 1.94 0.02 0.95 0.59 –0.53 1.49 0.45 2004 –0.95 –1.99–1.17 0.43 –1.71 –0.99–1.20 0.71 –0.34–2.37–0.86 2005 0.08 –2.86 –3.69 –1.67 –1.18 –2.34 –2.94 –0.45 –2.21 –2.06 –2.25 2006 2.21* 3.89*2.96 3.45*1.81 2.74 4.29*2.60*3.30*2.65 3.24*0.19 2.42*1.42–1.18 1.13 1.48*–0.84–0.37 3.32*2007 2.63* 1.72–1.39 2.12*1.57*1.62*3.03 2.17*1.98 1.28 1.51 2008 2.39* 3.28*2.27 2.59*1.78 2.50*4.21*2.45*3.43*2.02*1.53*2009 1.43 1.33 2.90*2.52*2.07*2.04*2.17*2.82*2.34 2.39*1.59均值 1.00* 1.01*1.94 1.36*1.06*1.13*1.34*1.27*1.27*0.98*0.87*3.00*4.09*2.44*1.33*平均市值 819.28 1675.98 618.39 3.31*–0.41–0.40 2.22*1.78 1.73 2.59*1.24–0.73–0.88 2.36 1.97*2.26*1.75*1.24*1812.341651.62 322.461159.77 2098.91 999.77 2651.86 4069.96 634.87 2004.94

三、欧洲市场的规模溢价

表2结果表明小公司的均值介于丹麦的18.05百万欧元到西班牙的63.96百万欧元间。西班牙小公司平均市值高的原因是该国适宜证券的数量少。其他样本国家，小公司平均市值很接近。对于整个市场小公司组合月均收益率是正值，介于英国的0.95%到希腊的2.93%间。此外，除希腊和英国外的所有市场的组合月均收益率都在5%水平上显著。这项按年进行的分析报告表明，这可能是这些市场小公司收益率高且具有统计显著性的年份多的结果。例，奥地利19个样本年有4年收益率是正值且显著。表3显示13个样本市场的大市值组合。整个样本期月均收益率显著且是正值（希腊除外），介于0.87%（英国）和1.94%（希腊）间。同样，年度分析报告表明，这可能是这些市场大公司的收益率高且显著的年份少的结果。例，英国的大股票组合19个样本年内，只有4年在5%的水平上显著。

SMB股票组合的收益率表明：（1）SMB股票组合的月均收益率介于德国的-0.03%和希腊的1%间；（2）在13个市场只有2个市场（法国和西班牙）的收益率具有5%的显著性水平；（3）整个样本期间极少数年份SMB股票组合的收益率具有统计显著性：例，在西班牙市场，收益率在19年中有3年显著。结果表明，虽然欧洲小公司股票组合的平均收益率比大公司高，但这种差异并不显著且在每个市场只限于极少年份。

四、规模溢价和零截距假说

迄今为止的结果似乎显示，虽然小公司组合收益率在所有市场都是正值，但可能不会连续高于大企业组合收益率。正如Brennan and Xia（2001）认为，资产定价异常是统计上的显著差异，该差异介于与具有某种特征的证券相关的已实现的平均收益率和特定资产定价模型预测的收益率之间。例如，夏普-林特资本资产定价模型认为预期超额收益率一定与市场贝塔系数线性相关：

公式（1）中，Ri是资产 i的收益率，Rf是无风险收益率，RM是市场组合收益率。Fama和French（1996）认为，资本资产定价模型被破坏时，必须在统计上拒绝对市场超额收益率进行回归的零截距假设。例如，Fama和French（1998）对全球价值和增长组合进行了相似回归并发现截距显著，这表明，国际资本资产定价模型不能解释全球组合的收益率。为了进一步调查该问题，我们假设公式（1）适用于三个证券组合（小，大，SMB）及以下所有国家：

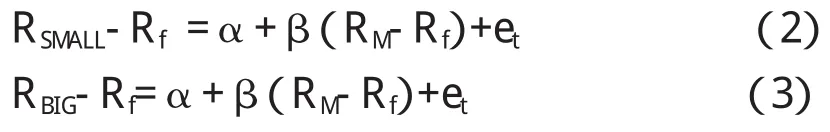
公式（2）、（3）及（4）中 RBIG是大市值公司组合收益率，RSMALL是小市值公司组合收益率，RSMB是套利组合收益。无风险收益率可用月国库券利率代替。奥地利、丹麦、爱尔兰、荷兰和挪威没有提供国库券利率，我们用月银行同业拆借利率代替。希腊、意大利、挪威、瑞士和英国用DataStream TotalMarket指数替代市场组合，对于其他市场我们使用代表性市场指数的总收益率指数。在5%水平上丹麦、法国、爱尔兰和西班牙的小公司股票组合拒绝零截距假设。在同样水平上所有市场的大公司股票组合接受该假设。在5%水平奥地利、丹麦、法国、挪威、西班牙和瑞士的SMB股票组合拒绝了零截距假设。

普通最小二乘法下的公式（1）会假定在整个估计期间存在常数斜率系数（即系统风险）。这种假设不可能在实践中长期存在。所以我们使用窗口长度为12和24个月的滚动最小二乘法而不是以往研究中仅用普通最小二乘法来估计公式（2），（3）及（4）。这允许系数估计超过连续滚动的定长周期并获得斜率系数和截距更充分的时间变化。对所有市场和组合，滚动最小二乘法过程生成了斜线和截距的系数表。我们发现，所有组合和市场的截距都不显著。即当估计期间系统风险常数假设解决后，零截距假设被所有样本市场接受。虽然这意味着，截距并不显著，但产生的估计可能不固定。我们用增广Dickey–Fuller检验测试估计滚动截距的平稳性，发现在5%水平上多数市场拒绝单位根零假设，整个市场是10%。本部分表明，欧洲小公司溢价基本不存在，且可能被静态（多数市场）或动态（所有市场）资本资产定价模型解释。

五、一月效应

以前的研究将规模效应和1月股票的季节收益率联系起来。为进一步研究此问题，我们重新估算所有组合和所有市场的（1）1月平均收益率，及（2）2月至12月的平均收益率。

例如，法国小公司组合1月份的平均收益率是6.23%，t检验值是4.31，而2月到12月的平均回报率是1.72%，t检验值是5.72。需要注意，虽然小公司组合1月和2月到12月的收益率在统计上都显著，但是1月份收益率更高：在1月份，收益率介于2.72%（瑞士）到10.73%（瑞典）间，而2月到12月的投资收益率介于0.63%（英国）到2.77%（希腊）之间。尽管1月份收益率比剩余月份的收益率均值大，但是认为1月份收益率与2月到12月平均收益率相同的零假设的成对t检验值表明相等性不会被任何样本市场拒绝。所以，尽管1月收益率具有明显的经济显著性，但是在统计上与该年剩余月份的收益率并无明显区别。

大公司组合1月收益率也是类似结果。除希腊1月与法国2月-12月外，所有时间与市场都符合收益率的统计显著性检验。与小公司组合一样，大公司组合也存在“1月效应”：1月大公司组合的收益率介于2.49%（瑞士）与5.23%（挪威）间，而2月-12月的收益率介于0.64%（英国）和1.81%（希腊）间。这意味着欧洲“1月效应”不限于小公司组合。SMB组合提供了更多的证据支持这一点。1月，13个欧洲市场中只有6个市场SMB组合的平均收益率有统计显著性。这些发现表明1月收益率会较高，但这较高的收益率并非只存在于小公司组合。

六、欧洲市场的动因收益

数据中可以发现一个有趣现象：整个样本期内所有组合极少年份具有统计显著性。以盈利组合为例，就平均水平而言，所有市场都具有统计显著性，但只有极少年份的月均收益率才具有统计显著性：英国的盈利组合19年中只有5年具有显著性，法国盈利组合19年中只有8年具有显著性，德国的19年中只有7年具有显著性等。若对WML组合进行观察，这种趋势更明显：除英国WML组合19年中有9年具有统计显著性外，所有样本市场均只有5年甚至更少的显著动量收益率：法国19年中有4年的WML组合具有显著收益率，希腊19年中只有1年的WML组合具有显著收益率等。与规模溢价数据相似，这些发现表明：早前研究所记录的动量收益只受到了极少年份显著性动因收益的驱动。

我们还对盈利、亏损与WML组合收益率的1月季节性进行测试并重新估计（1）1月份与（2）2月份-12月份月均收益率的均值，发现，盈利组合和亏损组合的1月份月均收益率远大于样本市场当年其余月份的收益率：盈利组合1月份平

均收益率介于3.90%（德国）到9.47%（挪威）间，而全年其它月份平均收益率介于1.08%（德国）到2.95%（希腊）间；亏损组合1月份平均收益率介于1.46%（奥地利）到12%（瑞典）间，而全年其它月份平均收益率介于0.22%（英国）到1.56%（希腊）间；WML组合1月份只有2个样本市场具有显著性且是正值，而从2月份-12月份有7个市场的平均动量收益有统计显著性且是正值。无论是盈利组合还是亏损组合，1月份收益率都比当年其它月份的平均收益率更具有统计显著性，所以，WML组合1月份收益率明显偏低。但是成对的t-检验表明任何样本市场都不能拒绝1月份收益率与2月份-12月份平均收益率间的相等性。

七、动因收益与零截距假设

本部分将用公式（2）、（3）、（4）中所示的普通最小二乘法与滚动最小二乘法，通过盈利、亏损和WML组合的回归分析，对每个国家市场组合的超额收益进行零截距假设检验。研究结果表明：（1）静态CAPM模型（普通最小二乘法）不能在5%显著水平对欧洲13个样本市场中的7个市场的盈利组合收益率作出解释；（2）静态CAPM模型能对除法国外的所有市场的亏损组合收益率作出解释；（3）静态CAPM模型不能对欧洲13个样本市场中的7个市场的WML组合收益率作出解释（奥地利，法国，德国，希腊，意大利，荷兰和英国都以5%的显著性水平拒绝零截距假设）；（4）动态CAPM模型能对所有市场盈利、亏损与WML组合做出充分解释（所有市场均不能拒绝零截距假设）。增广Dickey–Fuller检验表明，所有市场均能以10%的显著性水平支持零截距假设，其中大部分市场可以达到5%的显著性水平。

八、时变β值和经济周期

结果表明，虽然静态CAPM模型不能很好解释组合的规模收益与动量收益，但是动态CAPM模型可以。为说明时变β值，研究人员常把β作为延迟宏观经济变量的函数。尽管使用不同方法研究时变β值，但有一个共同点：β值变化CAPM模型可对股票收益率的截面数据作出准确解释。为了进一步探讨本问题，本文将测试欧洲股票组合中的时变β值是否与经济周期相联。与以前学者不同的，本文没有对β值的产生过程进行任何假设；以前的研究都把有条件的β值放入其特定结构，这是文献资料对于显著性会出现分歧的原因。尽管为了推导有条件CAPM模型，对产生β值的过程作出假设是有必要的，但是这增加了模型误设的风险。检验哪种模型具有最好分析能力已经超出本文研究范围。本文关注的是时变β值是否与经济活动相关。为此，本文用与经济周期相关的一套宏观经济变量对滚动β预估值进行回归。本文使用三个变量：（1）3月期国库券利率；（2）市场股利率；（3）期限差异，即10年期政府债券利率与3月期国库券利率间的的差额。因此，我们对每个国家均使用以下公式估算：

公式（5）中，RBT是SMB和WML组合β值的滚动估计值，DYT是股利率，DYt是3月期国库券利率，TERMt是期限差异，用10年期政府债券利率与3月期国库券利率间的差额计算得出。

很明显，多数国家的系统风险和实体经济有关。多数国家至少有一个重要宏观经济变量在5%的水平上显著。例如，奥地利，丹麦，法国，德国，希腊，意大利，荷兰和英国的WML组合β值的股利率系数具有统计显著性。这似乎表明，系统风险（某种程度上）随经济周期而变化，因此这个时间变化可能就是静态CAPM模型不能解释已实现收益率的原因。

九、结 论

本文对不同规模、不同市场发展与不同市场微观结构的欧洲普通股大样本的小公司溢价与动因溢价展开研究。本文发现SMB组合的平均月收益率介于0.03%（德国）与1%（希腊）之间，并且13个样本中只有2个具有统计显著性，而WML组合的月平均收益率介于0.37%（西班牙）到13.7%（希腊），并且13个样本中只有8个具有统计显著性。说明显著性时变的发现是，SMB组合与WML组合的收益率都要归因于收益率大且具有统计显著性的极少年份。此外，SMB组合收益率与13个市场中的7个市场静态CAPM模型一致，WML组合收益率与13个市场中的6个市场静态CAPM模型一致。所用方法考虑到系统风险中的时间变化，对所有样本市场，SMB组合与WML组合收益率都与CAPM模型一致。本文还指出系统风险可能与经济周期有关。

总之，本文证实了小公司溢价较为有限而动因溢价却较为可观的前人研究结论。因为我们的样本期溢价只是由于少数年份，而且组合收益率与时变β值一致，所以，利用这些“异常”是另外一件事。因此CAPM模型的静态结构可能就是早期研究拒绝该模型以及股票收益率与系统风险预估值不一致的背后原因。

［1］ Chordia,T.,and L.Shivakumar,2002,“Momentum,business cycle,and time-varying excepted returns”,Journal of Finance 57,pp.985～1019

［2］Fama,E.F.,and K.R.French,2006,“The value premium and the CAPM”,Journal of Finance 61,pp.2163～2185

［3］ Goetzmann,W.N.,A.Watanabe,and M.Watanabe,2009,“Investor expectations,business conditions and the pricing of beta-instability risk”,Yale ICF working paper（International Center for Finance,Yale School of Management,New Haven,CT）

［4］Ince,O.S.,and R.B.Porter,2006,“Individual equity return data from Thomson DataStream:handle with care”,Journal of Financial Research 29,pp.463～479

［5］ George Karathanasis,Konstantions,and Spyros Spyrou,2010,“Size and momentum in European stock markets:empirical findings from varying beta Capital Asset Pricing Model”,Accounting and Finance 50,pp.143～169

［6］严明义，吴诣民.证券组合投资的统计分析[J]，统计与信息论坛，2000，15（4）：2-29

［7］陈浪南，屈文洲.资本资产定价模型的实证研究[J]，经济研究，2000，4：26-34

［8］王敬，张莹.行为资产定价模型的适应性研究[J]，价值工程，2006，1：119-121

［9］ Bekaert,G.,C.B.Erb,C.R.Harvey,and T.R.Viskanta,1997,What matters for emerging equity market investments,Emerging Markets Quarterly 1,17–46

［10］Ang,A.,and J.Chen,2007,The CAPM over the long run:1926–2001,Journal of Empirical Finance 14,1–40

［11］ Bhandari,L.C.,1988,Debt/equity ratio and expected common stock returns:empirical evidence,Journal of Finance 43,507–528

［12］ Bagella,M.,L.Becchetti,and A.Carpentieri,2000,The first shall be last.Size and value strategy premia at the London Stock Exchange,Journal of Banking and Finance 24,893–919

［13］ Banz,R.W.,1981,The relationships between return and market value of common stocks,Journal of Financial Economics 7,3–18

［14］ Basu,S.,1983,The relationship between earnings yield,market value,and return for NYSE common stocks:further evidence,Journal of Financial Economics 12,129–156

［15］ Basu,D.,and A.Stremme,2007,CAPM and time-varying beta:the cross-section of expected returns,working paper[online;cited 5 May 2009].Available:http://papers.ssrn.com/sol3/papers.cfm?abstract_id=972255