基于Gaussian－支持向量回归机的高速公路短时交通量预测＊

赵泽辉 康海贵 李明伟 周鹏飞 莫仁杰

（大连理工大学工程建设学部1） 大连 116024） （河南省济邵高速公路有限公司2） 济源 454600）

高速公路迅猛发展，以交通控制与诱导系统为核心的智能交通系统ITS［1］应运而生，而实现ITS的关键问题是实时准确的进行交通量预测［2］，是进行高速公路的路况分析、事件检测及预测和预防交通拥堵的先决条件.因此，对高速公路短时交通量的准确实时预测已成为高速公路智能化管理的一个重要环节.在短时交通量预测方面，大致可以分为两类：一类是基于确定数学模型的方法如时间序列预测模型和卡尔曼滤波模型等，另一类是基于知识的智能模型的预测方法如神经网络模型［3］、基于混沌理论的模型［4］等.支持向量回归机（support vector regression，SVR）采用结构风险最小化原则替代经验风险最小化原则，能根据有限的样本信息，在模型的复杂性和学习能力之间寻求最佳折中［5］，克服了神经网络算法存在的全局搜索能力差或易收敛于局部最小等缺陷［6］，在解决实时性、波动性和非线性问题中表现出许多特有的优势，应用于短时交通量的预测取得了较好的效果［7－8］.本文利用遗传算法（GA）进行Gaussian－SVR模型参数的优选，在预测过程中，综合考虑了预测路段前几个时段交通量、天气因素和出行日期的影响，结合长济高速公路某段西行方向的实测交通量进行仿真预测，并进行了对比分析.

1 基于Gaussian损失函数的支持向量回归机

1.1 ε－损失函数支持向量回归机

设已知训练集T＝｛（x1，y1），…，（xl，yl）｝.式中：xi∈Rd；yi∈R，i＝1，2，…，l，损失函数ε为：c（xi，yi，f（xi））＝｜yi－f（xi）｜ε，其 中：｜yi－f（xi）｜ε＝max｛0，｜yi－f（xi）｜－ε｝，此时基于ε－损失函数支持向量回归机问题为：

式中：ω为d维列向量；C（C＞0）为惩罚系数；ζ（＊）＝（ζ1，ζ＊1，…，ζl，ζ＊l）为松弛变量.

引入Lagrange函数

式中：乘子a（＊），η（＊）≥0，为求它的极小，分别对ω，b和ζ（＊）计算偏导数，并同时引入核函数K（xi，yi），整理后得到问题（1）的对偶问题为

1.2 Gaussian损失函数的支持向量回归机

设训练集T＝｛（x1，y1），…，（xl，yl）｝中的样本点是由一个基本函数依赖关系ftrue和噪声产生的，即

当噪声的密度函数p（ζi）已知，则在最大似然意义下，最优的损失函数是

证明对式xf≜｛（x1，y1），…，（xl，yl）｝的最大似然估计是

由式（5）和上式，得到

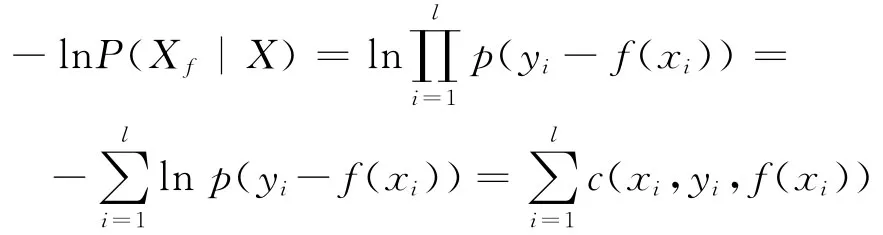
本文采用高斯函数进行降噪处理，此时噪声的密度函数为Gaussian函数，则有

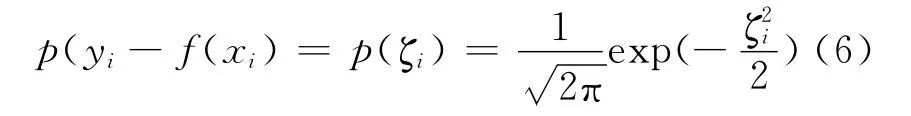
由式（5）知

此时，基于Gaussian损失函数的SVR为

式中：ω为d维列向量；C（C＞0）为惩罚系数；ζ（＊）＝（ζ1，…，ζl）为松弛变量.

基于Gaussian损失函数的SVR模型算法步骤为

步骤1设已知训练集T＝｛（x1，y1），…，

步骤2选择适当正数ε和C，以及核函数K（xi，yi），本文核函数选为径向基函数.

步骤3构造并求解最优化问题

得到最优解a（＊）＝（a1，…，ai；，…，）.

步骤4构造决策函数

式中：按下式计算，选择位于开区间（0，C／l）中的2个分量或，若选到的是，则

若选到的是，则

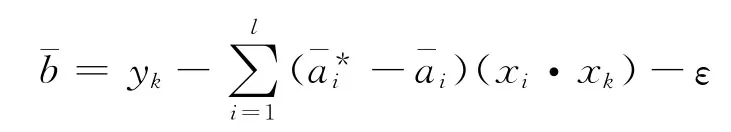
2 基于GA优化的Gaussian－SVR短时交通量预测步骤

考虑到Gaussian－SVR参数的选取在一定程度上影响着模型的精度，本文应用遗传算法对Gaussian－SVR参数ε，C和δ2进行优选.

以训练结束后返回的回归序列方差的倒数作为进化个体的适应值fitness

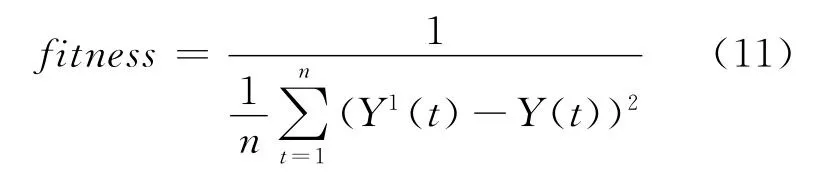
式中：n为输入样本个数；Y1（t）为回归序列；Y（t）为实际序列值.GA－Gaussian－SVR预测模型的计算步骤如下.

步骤1归一化处理.对实测量数据集和Gaussian－SVR参数的初始区间按式（12）进行归一化处理.

步骤2初始化父代群体.设种群规模为m，随机生成父代群体y（j，i）（j＝1，2，3；i＝1，2，…，m），本文取m＝50，其中y（j，i）为第i个父代染色体上的第j个基因.

步骤3模型训练.以生成的每个染色体上的基因作为Gaussian－SVR参数，训练Gaussian－SVR模型，计算相应的回归序列，并根据回归序列按式（11）计算染色体的适应度值.

步骤4终止判断.判断当前种群中最优个体是否满足终止准则，若满足转入步骤7，否则转入步骤5，进化代数g＝g＋1.终止准则采用最大进化代数Gmax与相邻进化代数最优个体适应值相对误差E相结合.

步骤5选择、交叉和变异.根据步骤3计算所得的染色体的适应度值，进行选择、交叉和变异操作.

步骤6生成子代新个体.由步骤5得到的3m个子代个体，按照其适应值fitness从大到小进行排序，取排在最前面的m个子代个体作为新的父代群体.转入步骤3进入下一轮演化过程.

步骤7模型预测.以当前种群中最优个体的染色体基因ε，和δ作为Gaussian－SVR参数训练模型，输入待测样本，输出预测值.

计算流程见图1.

3 实例预测与性能分析

3.1 高速公路交通量预测影响因素选择

图1 算法流程图

交通流具有流体的特性，在时间上的分布是连续的，某路段下一时刻的交通量与本路段前几个时段的交通量有着必然的联系，所以可以利用本路段前几个时段的交通量数据预测该路段下一时段的交通量，t表示交通量观测的当前时段，Y（t－3），Y（t－2），Y（t－1），Y（t）为预测路段前4个时段的交通量，Y（t＋1）为预测路段下一时段的交通量，因此，该路段t＋1时刻交通量Y（t＋1）的大小受交通量Y（t－3），Y（t－2），Y（t－1），Y（t）共同作用的影响.

考虑到高速公路通行在很大程度上受到天气变化的影响，引入第五个输入参数X1（t），X1（t）其量化方法为大雪或大雨雪为1，小雪或小雨雪为0.75，大雨为0.5，小雨为0.25，晴或多云为0.同时人们出行习惯也会对高速公路交通量产生影响，交通量以周为周期，在每周的不同天中，可能具有不同的变化规律，特别是在周末通行量会增多.因此，将出行日期作为模型的第六个输入参数X2（t）.其量化方法为周一为1／7，周二为2／7，周三为3／7，周四为4／7，周五为5／7，周六为6／7，周日为7／7.至此，得到了影响预测路段下一时段交通量的6个影响因素X，作为模型的的输入向量.

本文试验部分采用长济高速公路济源市内某路段西行方向的交通量检测仪于2009－06－01至2010－06－07一周内获取交通量数据，采集时段为10min，选取240组交通量数据并对其相应的天气和获取日期进行量化处理，组成模型训练样本集，选取40组数据作为测试样本集.

3.2 模型实例预测与性能分析

利用 Matlab 7.1编制 GA－Gaussian－SVR模型程序，运行环境为：Core（TM）2CPU，1.81 MHz，2GB 内 存 的 微 机，操 作 系 统：WindowsXP.模 型 初 始 值：C的 取 值 范 围 为 ［1，2 000］，ε的取值范围为［0，2 000］，δ的取值范围为［0，20］，最大进化代数Gmax＝1 000，邻代最优个体适应值相对误差E＝0.000 1.应用本文提出的模型，经过训练得到全局参数最优组合为C＝213，ε＝41和δ＝0.23.将优化后的模型用于测试样本集的交通量预测.实际交通量与模型仿真输出流量的对比图和部分实际交通量与模型预测结果见图2和表1，结果表明，预测结果曲线与实际交通量的变化曲线基本吻合，绝对误差值基本控制在［－7，7］区间内，只有少量超出这个范围，预测结果达到了预期的预测效果.

图2 GA－Gaussian－SVR模型训练效果图

表1 部分实测流量与模型预测流量结果pcu／（10min）

为了比较GA－Gaussian－SVR模型的预测性能，本文选择文献［3］提出的PSO－BP神经网络模型、文献［8］中提出的 WA－SVM预测模型和文献［7］提出的G－SVR预测模型进行对比分析.为了使对比模型具有可比性，4个模型均在同一台微机上进行计算，均使用matlab 7.1进行编程.考虑到寻优次数的增加也会提高优化效果，对比模型参数的选取应保证每个模型的最大寻优次数相同，对PSO－BP神经网络模型优选次数的设定，应综合考虑PSO算法和BP神经网络的寻优次数，保证与GA算法具有相同的最大优选次数，对WA－SVM预测模型参数的选择，进行多次交叉试算，尽可能的保证SVR参数的选择精度.并采用以下3个评价指标进行性能对比分析

1）平均绝对相对误差

2）最大绝对相对误差

3）均方根误差

设定对比模型参数，结合实测交通量数据分别进行模型训练，并对测试样本进行预测，将预测结果分别进行误差指标处理，处理结果如表2所列.

表2 预测误差指标比较 %

从表2中可以看出，在逼近原始流量序列的能力方面，SVM的预测方法明显优于PSO－BP神经网络模型.在对基于不同损失函数的SVM比较方面，采用高斯损失函数GA－Gaussian－SVR模型的误差指标值均优于GA－SVR模型，说明在交通量序列中存在着成正态分布的噪声，基于Gaussian损失函数的Gaussian－SVR模型对序列中的噪声进行了有效的处理，提高了模型的预测精度.在对噪声处理比较方面，本文提出的模型的预测精度略低于 WA－SVM模型，但小波分析过程复杂，不利于ITS系统自动操作，特别是对于实时交通量预测而言，在保证一定精度的范围内，操作的复杂程度和时间消耗更值得关注，从这个意义上讲，本文提出的模型更适用于高速公路短时交通量预测.

4 结束语

从上述实例对比分析中可以看出：采用结构风险最小化原则的SVR模型克服了神经网络模型存在的全局搜索能力差或易收敛于局部最小等缺陷，取得了较好的预测效果，Gaussian损失函数的引入弥补了SVR模型无法对序列内噪声进行有效处理的不足，从而进一步提高了模型的预测精度.针对运行时间开销主要取决于模型参数的寻优阶段，应用GA进行Gaussian－SVR模型参数的优选，缩短模型寻优阶段的时间，提高寻优效率，更适合于系统一定时段内，利用新的数据进行模型参数的自动更新.在预测过程中，本文综合考虑了长济高速公路西行方向前四个时段的交通量、天气和出行日期6个因素的影响，为对交通量进行精确预测提供数据保障，实例分析过程中，实测流量与模型预测流量非常接近，达到了模型的预期效果，表明该模型适用于对高速公路短时交通流的预测.

［1］Mark D B.Peering into the future：peer－to－pee technology as a model for fistributed joint battlespace intelligence dissemination and operational tasking［D］.Maxwell Field，Alabama，USA：PhD＇s Thesis of School of Advanced Airpower Studies，Air University，2001.

［2］David P J.Rationality and self－interest in peer to peer networks［A］.Proceedings of the 2nd International Workshop on Peer－to－PeerSystems IPTPS＇03［C］／／Claremont Hotel， Berkeley， CA， USA：Springer press，2003.

［3］叶 嫣，吕智林.基于粒子群优化的神经网络短时交通流量预测［J］.计算机工程与设计，2009，30（18）：4 296－4 299.

［4］郭 敏，蓝金辉，肖 翔，等.基于混沌理论对北京二环路进行短时交通流量预测的研究［J］.交通运输系统工程与信息，2010，10（2）：107－110.

［5］Vapnik V.The nature of statistical learning theory［M］.New York：Springer，1995.

［6］Cao J R，Cai A N.A robust shot transition detection method based on support vector machine in compressed domain［J］.Pattern Recognition Letters，2007，28（12）：1 534－1 540.

［7］任其亮，谢小淞，彭其渊.城市道路交通量短时预测的GSVMR模型［J］.公路交通科技，2008，2（52）：135－138.

［8］朱胜雪，周 君，包 旭.基于小波分解－支持向量机的短时交通量预测［J］.苏州科技学院学报：工程技术版，2007，20（3）：80－85.