不同温度下沥青混合料劈裂强度的影响因素*
陆学元 张素云
(安徽省高速公路控股集团有限公司1) 合肥 230051) (安徽交通职业技术学院2) 合肥 230051)
0 引 言
沥青混合料力学性能随着温度的变化表现非常复杂,当气温急剧降低,沥青混合料刚性显著增大,其模量远大于半刚性基层模量,沥青层底拉应力增大,在拉应力和剪应力的共同作用下行车带轮迹边缘附近容易产生拉裂,同时若温度收缩应力超过沥青混合料破坏强度路面将发生开裂[1-2];高温状态下沥青混合料强度急剧衰减,在车辆荷载作用下,路面产生水平应力超过沥青混合料抗剪强度易出现车辙、变形等病害[3].可见,沥青混合料强度直接影响沥青路面的路用性能与使用寿命.国内外学者从不同角度研究探讨了沥青混合料劈裂强度及其劈裂强度对路用性能的影响问题[4-6].以往的研究对表面层沥青混合料劈裂强度探讨较多,对AC-25热拌沥青混合料劈裂强度问题研究及其在不同温度条件下的力学性能演变规律探讨则很少.本文结合前人研究成果,探讨涵盖粗型和细型级配的AC-25沥青混合料劈裂强度影响因素问题,以揭示不同温度下AC-25沥青混合料劈裂强度的影响规律,对提高道路的综合路用性能提供借鉴指导作用.
1 试验设计与试验结果
粗集料为石灰岩,细集料为石灰岩机制砂,填料为矿粉;结合料采用70号A级沥青.技术指标均符合文献[7]要求.采用正交试验设计方法.考虑5因素(分别以A,B,C,D,E表示)和5水平,因素水平选取见表1.每组级配通过率符合正交表L25(5)6规定要求,见表2.以马歇尔成型为技术手段,成型温度为(152±2.5)℃,理论最大相对密度由真空法实测得到.每组有效试件12个,每4个试件分别用于0,15,45℃劈裂试验使用.劈裂试验仪器为LDR-2型沥青混合料冻融劈裂仪,技术参数为最大荷载50kN,荷载范围5~35kN,加载速率为(50±5)mm/min,并配有试验环境箱.按照规程方法试验,结果见表2.
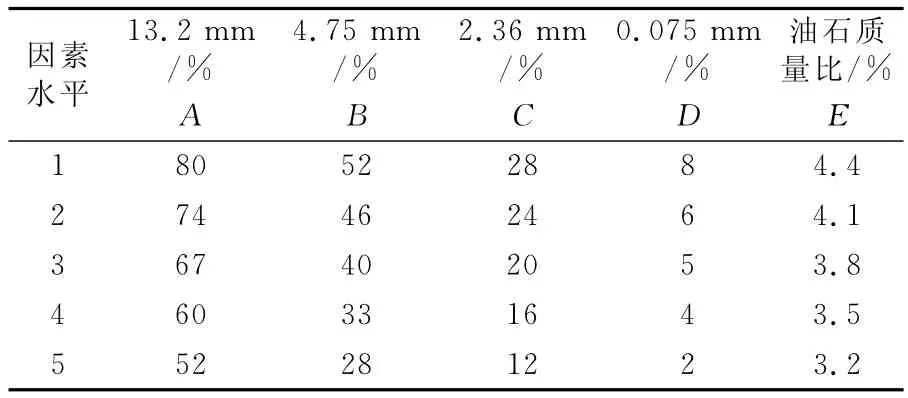
表1 正交试验设计因素水平表

表2 设计方案与试验结果
2 结果分析
2.1 方差分析
方差分析法是将因素水平变化引起的试验结果间的差异与误差波动引起的试验结果间的差异区分开来的一种数学方法,可以对各因素的显著性水平给出一个定量分析,基本过程如下.
检验各因素水平的变化是否对劈裂强度有显著影响,是检验式(1)的假设.

对检验式(1)进行方差分析,将数据的总变差中区分出试验误差和条件变差(试验结果间的差异),并赋予它们的数量表示,即分解为各因素响应值之和、响应值均值和响应值的平方和(式(2));各因素对应水平响应值的平方和均值(式(3));各因素引起的离差平方和和总离差平方和(式(4));试验误差(式(5)),以进行统计检验.

引入自由度的概念可消去数据个数的多少给平方和带来的影响.总平方和自由度为n-1=24,每个因子引起的离差平方和的自由度为4,而误差自由度为n-1-r1(s-1)=25-1-5(5-1)=4,其中(r1≤r).用各因素离差平方和除以相应自由度所得的商称为均方离差.若式(1)的假设成立,均方离差的期望值相同,则有FA=(QA/4)/(QE/4),等等.由此式来检验式(1).即当式(1)假设成立时,F应服从F(s-1,n-1-r1(s-1))分布,从而小概率事件取在F值大的一侧较为合理.
以0℃劈裂强度影响因素E为例分析.K=(2.688+2.669+…2.65+4.03)=55.165,W=(2.6882+2.6992+ … +2.652+4.032)=123.84,K1=(2.688+2.01+2.366+2.142+2.65)=11.856,K2=(2.669+2.042+2.476+1.618+2.403)=11.208,K3=(2.325+2.306+2.192+2.321+1.86)=11.004,K4=(2.084+2.281+1.664+2.423+2.018)=10.47,K5=(1.737+1.987+2.27+2.131+2.502)=10.627,=140.565,=125.619,=121.088,=109.62,=112.93;UE=(++++)=609.826;P=K2/25=121.727,QE=UE-P=488.09;QT=W-P=2.115,误差QE=QT-QA-QB-QC-QD-QE.均方离差S=QE/4=0.059 7,F分布值=S/QE=3.969 2.给定显著性水平α=0.05,0.01,则F0.05(4,4)=6.39,F0.01(4,4)=15.98.从而0 ℃劈裂强度方差分析结果如表3。同理,15℃劈裂强度和45℃劈裂强度方差分析结果如表4.

表3 0℃劈裂强度方差分析结果

表4 15℃与45℃劈裂强度方差分析
2.2 极差分析
正交试验设计方法的试验因素均在变化,采用极差分析方法是判定因素影响主次的技术手段之一,极差是指各因素不同水平的试验结果间的最大差值.设因素个数为N,序号为j=1,2,…,N;每个因素水平数为M,水平序号为r,r=1,2,…,M,同一水平只能作M次试验.Ka为对应于各因素相应水平的不同温度劈裂强度试验结果,即评价指标;Kj为j因素N分别在同一r水平下Ka值之和的平均值,反应因素在该水平效应的大小.将同一因素各水平效应逐一进行比较,即可找出最佳和最差水平,从而求出极差:

将各因素的极差进行比较,由极差大小顺序可判定各因素的影响大小;通过各因素在不同水平的Kr值作因素水平与评价指标Ka之间的关系曲线,可得出各因素的影响程度和相应水平试验结果的影响趋势.不同温度下劈裂强度极差分析结果见表5.

表5 不同温度下融劈裂强度极差分析结果
1)由表3、表4可见,不同温度下劈裂强度的影响因素大小排序均为C>D>A>E>B.其中,2.36mm通过率对不同温度下的劈裂强度影响高度显著,其次,0.075mm和13.2mm通过率的影响也较为显著,而4.75mm通过率对不同温度下的劈裂强度影响较小.试验结果表明,不同温度下AC-25沥青混合料劈裂强度的影响因素程度并没有随试验温度的变化而发生排序上的改变,但影响程度有所差异.其中,2.36mm筛孔通过率是影响0,15和45℃劈裂强度最关键因素,且随着温度的逐渐升高,2.36mm筛孔通过率劈裂强度的影响愈加明显,表明由压应力转化为拉应力受力模式下的劈裂强度随温度的逐渐升高,沥青混合料的内部结构组成决定了抵抗劈剪的宏观力学性能.
2)不同温度劈裂强度并没受到事先设计级配区间越大而表现出较大影响,如尽管2.36mm和0.075mm通过率变化较小,但对劈裂强度影响却很大.说明矿料级配对不同温度下劈裂强度起支配地位,尤其是细集料级配对其影响很大.
3)对比表5与表3、表4可知,不同温度劈裂强度的各因素影响大小排序相同,表明作为直观分析的极差分析,每个因素各水平对应试验结果间的差异是因素水平变化所引起,并是试验误差所致,即来自12×25=300个母体总体的试验结果并不是试验误差造成.结合表5极差分析结果可知,当2.36mm通过率由12%增至28%时,0℃,15℃和45℃劈裂强度分别单调增加20%、25%和32%.
综上所述,各因素所在列的差异实际上只反映该因子由于水平变动引起指标的波动,并不受到相邻因子变动而改变,试验结果证明了不同温度劈裂强度值主要受控于矿料级配,优化级配不仅可提高路面高温抗变形能力,也有助于提高中温条件下沥青路面的抗疲劳性能.
3 结 论
1)不同温度下AC-25沥青混合料劈裂强度影响因素的程度大小排序为2.36mm通过率>0.075mm通过率>13.2mm通过率>油石质量比>4.75mm通过率(C>D>A>E>B);影响不同温度劈裂强度的因素没有随温度的变化而发生改变,只是其影响程度有所不同.随温度的逐渐升高,2.36mm筛孔通过率的影响越加显著,说明优化2.36mm通过率可明显提高路面的抗劈剪抗拉能力.
2)不同温度下劈裂强度并没有受到事先设计级配区间大小而发生较大变化,尽管考察因素4.75mm通过率变化24%,对劈裂强度影响并不明显,而2.36和0.075mm通过率变化分别只有16%和6%,却对劈裂强度影响显著.当2.36mm通过率由12%增至28%时,不同温度下劈裂强度分别单调增加20%,25%和32%.这与以前研究规律一致[8-9].
3)方差与极差分析结果表明,2种数理统计分析结果是一致的,极差分析对因子(因素)作用的判断并不是由于试验误差引起的,而是因子本身对实验指标有显著影响.表明正交试验设计考核的各影响因素中,集料级配的变化对不同温度下劈裂强度值的影响较油石比影响更大.
[1]魏建国,查旭东,郑健龙,等.大粒径沥青混合料基层结构抗裂机理分析[J].公路,2008,4:1-5.
[2]皮育晖,张久鹏,黄晓明,等.沥青混合料劈裂试验数值模拟[J].公路交通科技,2007,24(8):1-6.
[3]李晓军,王贵荣,冯 樊.考虑非均匀性的沥青混凝土间接拉伸强度测定仪研制与应用[J].武汉理工大学学报:交通科学与工程版,2010,34(2):310-313.
[4]李好新,索 智,王培铭.不同空隙率沥青混合料的形变及破坏[J].建筑材料学报,2008,11(3):306-310.
[5]张 雷,陈静云,乔英娟,等.间接拉伸试验条件下沥青混合料变形特性[J].辽宁工程技术大学学报:自然科学版,2008,28(6):856-858.
[6]彭 勇,孙立军,石永久,等.沥青混合料均匀性与材料力学性能关系,哈尔滨工业大学学报,2009,41(6):142-145.
[7]中华人民共和国交通部.JTG F40-2004公路沥青路面施工技术规范[S].北京:人民交通出版社,2004.
[8]陆学元,张治锋.AC-25沥青混合料矿料级配优化与应用研究[J].中外公路,2009,29(2):207-213.
[9]陆学元,孙立军.AC-13改性沥青混合料劈裂强度的影响因素及其与马歇尔性能指标的相关性[J].吉林大学学报:工学版,2010,40(3):666-682.

