基于衰减因子的时变增益KALMAN滤波＊

周 浩 胡科强

（海军工程大学兵器系 武汉 430033）

0 引 言

在浮标基阵数据融合系统中，目标跟踪、数据关联、航迹关联和数据融合是面临的主要问题［1－3］.而目标定位跟踪是解决其他问题的基础.目标定位跟踪的关键在于运动模型和跟踪算法.目标跟踪对实时性具有较高要求，需要兼顾计算复杂度和算法的有效性，而状态估计［4－5］是其中关键一环，常用的卡尔曼滤波器（KF，EKF）一般只适用于平稳的状态过程，当目标处于变化不大的过程时，目标状态突然变化时，KF和EKF将产生较大的估计偏差，甚至丢失目标.

本文根据正交性原理，采用时变衰减因子，使得残差达到正交或近似正交，从而使滤波器在不确定模型下保持较好的鲁棒性.通过实时调节增益，促使测量残差近似正交，从而提高对机动目标的跟踪性能.

1 问题分析

图1模拟了位于（－380，200m）位置的目标以38kn的速度匀速直航到（380，200m）坐标位置时方位角变化过程，方位角定义为偏北方向夹角，顺时针为正.测量浮标位于坐标原点位置，从图中可以看出方位角在第15～25s时发生跃变.以上目标模型与卡尔曼滤波方法在目标逼近浮标时即方位角近似跃变时对方位角的状态估计效果恶化.

图1 方位角变化曲线

图2 为实际测量目标方位角与目标方位角估计值对比图，图3为实际测量目标方位角与目标方位角估计值的误差示意图.可以看出目标状态平稳时基本保持良好跟踪性能.当方位角发生跃变时，滤波效果恶化.为解决这个问题提出了基于衰减因子的EKF滤波方法.用于改善系统线性化误差和滤波发散问题.

图2 限定下限的KF滤波效果

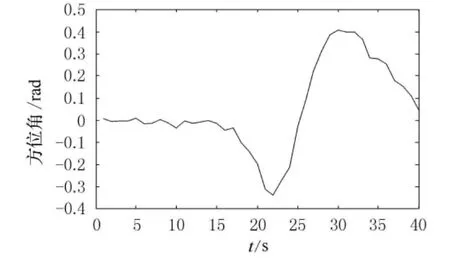
图3 限定下限KF滤波误差

2 基于衰减因子的时变增益模型

卡尔曼滤波是增长记忆滤波［6－7］，一般情况下它给出了一个随着观察资料的积累精度不断提高的估计.估计误差协方差的范数随着时间的增长不断减小，因此新的观察资料对修正状态估计的作用逐渐减弱.但是，实际上系统动态模型的变化规律是很难在事前完全知道的.这样，一方面这些系统的参数在变化，另一方面，在递推过程中还是把这些已经变化了的参数当作精确值来进行运算.文献已经证明［8］：（1）当模型与实际系统完全匹配KALMAN滤波的输出残差序列是不自相关的高斯白噪声序列.（2）当系统达到稳态并且KF也达到稳态时，KF的预报误差协方差P（k｜k－1）也趋于极小值，从而导致K（k）也趋于极小值.此时，当状态X（k）发生突变时，就会导致残差增大，但P（k｜k－1）和K（k）并不能随之增大，因此KF基本丧失对突变状态的跟踪能力.

由于新近的观察资料含有变化了的系统动态模型的较多信息，在滤波器中须增强这些新观察资料对修正状态估计误差的作用，降低老的观察资料的地位.基于衰减因子滤波器就是基于这一考虑而提出的防止滤波器发散的方法.

条件（1）是KF滤波器的性能指标，条件（2）要求不同时刻的残差序列处处保持正交.在实际问题中，选择的模型不可避免存在不确定性，因此输出残差不可能白化.

本文从上述两条件出发，引进渐消因子λ（k），实时调节增益K（k），强制输出残差近似为高斯白噪声，最大程度地提取输出残差中的一切有效信息.

在KALMAN滤波的基础上引入衰减因子，构成衰减记忆KF滤波器，采用Tarn和Zaborsky提出的一种简单实用的引入衰减因子的方法［9］.加入衰减因子S，使预测协方差变为

在仿真中发现，衰减因子的选取会对滤波结果产生很大影响，引入衰减因子后的滤波将使估值的方差增大，且衰减记忆滤波的精度随S的增加而降低［10］，在一些情况下可能会发生异常，甚至导致滤波发散.为此，在加入衰减因子的基础上，再引入一个自适应因子.更新误差协方差表示为

式中：αk为自适应因子，0＜αk≤1.

合理的自适应因子能够自适应地平衡状态方程与观测信息的权比，还能够控制状态模型扰动对滤波解的影响.αk构造为［11］

式中：V（k）为预测残差.

由上述分析可知，当初值选取不合理或模型存在异常扰动时，αk将小于1，即预测信息对滤波解的贡献将尽量小；当预测信息明显异常时，tr（VkVTk）将非常大，αk则将接近于0，即预测信息被完全弃用，从而有效控制了模型误差对滤波解的影响.

3 仿真计算与分析

对两种滤波方法进行对比仿真计算，试验的条件是：来袭鱼雷初始位置在（－380m，200m），航速38kn，浮标方位测量误差为高斯随机的，均值为0，测量方差为 ，采样间隔为1s.

在仿真中发现衰减因子S的选取对滤波结果影响很大，如图4所示，当选取S＝1.1时取得了较为理想的滤波效果，在仿真初始时刻滤波都有较大的偏差，这是由于初值的造成的.如图5所示，随着滤波的进行，当目标状态发生近似跃变时基于衰减因子的时变增益滤波较EKF算法提高了滤波收敛速度及滤波精度.

图4 基于衰减因子时变增益EKF滤波效果

图5 两种滤波误差比较

4 结束语

基于衰减因子的时变增益滤波增加了新测量值在状态估计中的权重，克服了EKF对旧测量值和初始值的依赖，且能够实时自动调整滤波增益，具有一定的自适应能力，可以实时检测滤波异常，有效控制初始偏差和模型的异常扰动给滤波造成的影响，从而有效提高对机动目标的跟踪性能.

［1］Yang Yuanxi，Gao Weiguang.A new learning statistic for adaptive filter based on predicted residuals［J］.Progress in Natural Science，2006，16（8）：833－837.

［2］孙仲康，周一宇，何黎星.单多基地有源无源定位技术［M］.北京：国防工业出版社，1996.

［3］周 浩，蒋兴舟，顾晓东.多声纳基阵时差定位无解问题研究［J］.武汉理工大学学报：交通科学与工程版，2006，30（6）：935－938.

［4］Fawcett J A.Effect of course maneuvers on bearingonly range estimation［J］.IEEE Transactions on Acoustics，Speech and Signal Processing，1988：36（8）：1 193－1 199.

［5］Jauffret C，Pillon D.Observability in passive target motion analysis［J］.IEEE Transactions on Aerospace and Electronic Systems.1996，32（4）：1290－1 300.

［6］王 燕.水下目标被动定位仿真研究［D］.哈尔滨：哈尔滨工程大学水声技术国防科技重点实验室，2000.

［7］石章松，周 丰，孙世岩.目标跟踪与数据融合理论及方法［M］.北京：国防工业出版社，2007.

［8］Ljung L.Asymptotic behavior of extended kalman filter as a pa2rameter estimator for linear systems［J］.IEEE Trans on Automat2ic Control，1979，24（1）：36－50.

［9］Tarn T，Zarbosky J.A practical non－driving filter［J］.AIAA Journal，1970，8（6）：1 127－1 133.

［10］张金槐.自适应衰减记忆滤波中时变衰减因子的最佳选择［J］.飞行器测控技术，1994（1）：9－13.

［11］Yang Yuanxi，Gao Weiguang.A new learning statistic for adaptive filter based on predicted residuals［J］.Progress in Natural Science，2006，16（8）：833－837.