基于VaR的中国有色金属 ＊期货市场风险测度研究——以上海期货交易所铝期货和铜期货为例

王泰强，侯光明，赵 宏

(1.北京理工大学 管理与经济学院，北京 100081;2.重庆理工大学 商贸信息学院，重庆 400054)

一、引 言

期货市场产生的初衷是为了规避现货市场价格波动的风险。然而，由于期货市场特殊的交易制度和运行规律，期货市场在规避了现货市场价格波动风险的同时，又引入新的风险。一方面，期货市场本身蕴藏着巨大的风险。期货市场参与者不仅有套期保值者，而且还有大量的投机者。期货的价格会因投机者的炒作而表现出更大的波动性。加之期货交易实行的是保证金制度，较小的资金就能够造成期货价格较大的波动。因此，期货市场价格往往比现货市场价格波动更为剧烈。另一方面，期货市场的价格波动可能会传递到现货市场，进而加大现货市场价格的波动性。比如，期货市场的价格因资金炒作出现了非理性上涨时，现货交易商可能会误认为未来需求将会出现明显增长，进而惜售现货，从而导致现货价格随期货价格上涨而上涨。为了充分发挥期货市场的积极功能，必须对期货市场价格波动的风险进行科学、有效的管理。风险管理的前提是对风险有比较准确的测度。因此，如何准确测度风险就成为期货市场风险管理的关键［1］。

本文利用VaR方法对上海期货交易所的铜期货和铝期货价格波动的风险进行测度，认识中国有色金属期货市场风险，为有效控制风险、制定科学投资决策提供依据。

二、风险测度的VaR方法

VaR(Value at Risk)被称为风险价值，最早由JP摩根公司提出，VaR方法主要用于金融领域市场风险的测度。该方法以其对风险测度的科学、实用、准确和综合的特点受到金融机构和金融监管部门普遍欢迎，目前已成为标准的风险测度和风险管理的方法。

VaR的一般定义可以表示为:在正常的市场条件下，给定置信水平下，某一金融资产或投资组合在某一特定时间内可能遭受的最大损失［2］。VaR用数学形式可以表示为:

其中，ΔPt为资产在持有期内的损失，VaRα为置信水平α下处于风险中的价值。从VaR的数学形式可知，VaRα实际上就是损失分布函数在置信水平α下的分位数。

目前，计算VaR的方法主要有历史模拟法、方差—协方差法和蒙特卡洛模拟法三种。其中，方差—协方差法因为收集数据容易、方法实现容易、计算速度快等优点在实践中得到广泛的应用［3］。这种方法基于线性假定和正态分布假定。然而，实际的金融数据序列通常具有尖峰厚尾、波动聚集的特征，一般不满足正态分布假定，导致该方法会低估实际的VaR值。为了克服方差—协方差方法的这一缺陷，研究者们提出了各种各样的方法:(1)改变正态分布的假定，考虑其他具有尖峰厚尾特征的分布，比如t分布、广义误差分布 (GED)等［4-5］。(2)利用GARCH族模型刻画金融时间序列波动聚集的特征，并基于GARCH族模型估计VaR［6-7］。(3)使用半参数方法估计VaR。(4)使用极值理论估计VaR。本文将利用基于GARCH模型和半参数方法对沪铜期货和沪铝期货价格波动的风险进行测度。

(一)基于GARCH模型的VaR模型

GARCH模型可以表示为:

其中，rt为收益率序列，μt为均值。rt=lnPt-lnPt-1，Pt为价格。

利用GARCH模型估计的条件方差σ2t，在一般的方差—协方差模型基础上，可以计算出价格波动的空头的VaR值和多头的VaR值:

其中，qα为α分位数。

(二)半参数VaR模型

Li［8］提出的半参数法不需做任何分布假设，只需计算收益率序列rt的偏度、峰度、均值和方差，即可构造VaR置信区间上限和下限。假设收益率rt为随机变量，其均值、方差、峰度和偏度分别为 μ=E(rt)、σ2=Var(rt)、γ1=。

若γ1=γ2=0，则rt服从正态分布。计算收益率的VaR值可以按照方差—协方差方法计算。若γ1≠0，γ2≠0，则rt不服从正态分布，可以证明VaR的置信下限VaR1和置信上限VaRu可用下面的公式计算得到:

其中，γ1≠0，Zα为显著性标准，即正态分布中α对应的分位数。

三、沪铝期货和沪铜期货市场风险的测度

(一)数据样本与统计特征分析

1.变量与数据

中国期货市场经历了一个由无序到有序的发展过程。1998年8月1日，国务院下发《国务院关于进一步整顿和规范期货市场的通知》。15家期货交易所被压缩合并为3家，交易品种由35个削减为12个，并提高部分品种的交易保证金。为了保持数据的一致性，本文选用1998年以后的数据进行研究。具体的样本区间为1999年1月4日至2011年7月29日。其中，沪铝期货样本总数为3 053个，沪铜期货样本总数为3 049个。由于期货合约一般都具有期限性，所以这里选用的是沪铝期货连续和沪铜期货连续收盘价的数据，相关数据来源于Wind数据库。

记沪铝期货和沪铜期货的价格分别为P1和P2，那么，它们的日收益率可以表示:

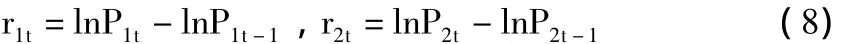
其中，r1t为沪铝期货的收益率，r2t为沪铜期货的收益率。

2.样本的统计特征分析

沪铝期货和沪铜期货合约的收益率如图1和图2所示，相关的描述性统计量如表1所示。从表1中JB统计量及其对应P值来看，沪铝、沪铜期货收益率序列均不服从正态分布。

图1 沪铝期货合约收益率时序图

图2 沪铜期货合约收益率时序图

表1 沪铝期货和沪铜期货合约收益率序列的描述性统计量

3.平稳性检验

利用ADF方法对收益率序列的平稳性进行检验。由检验结果 (如表2所示)可知，沪铝期货和沪铜期货收益率序列都是平稳序列。

表2 沪铝期货和沪铜期货收益率的平稳性检验

(二)基于GARCH-VaR的沪铝期货和沪铜期货市场风险的测度

从图1和图2的收益率时序图中可以发现，收益率序列存在波动聚集的现象。GARCH模型能够较好地刻画波动聚集的现象，因此，可以用GARCH模型来对收益率数据建模。另外，根据前文JB统计量可知，收益率序列不服从正态分布。这里假定收益率序列服从广义误差分布(GED)。GED分布的密度函数为:

假设均值方程和方差方程分别为:

利用沪铝期货和沪铜期货收益率序列估计上述的GARCH-GED模型，经检验，当使用沪铝期货收益率序列时，p=2，q=1;当使用沪铜期货收益率序列时，p=1，q=1。GARCH-GED模型的估计结果如表3和表4所示。从估计结果可知，GED分布的自由度的估计值分别为0.975和1.215，均小于2，这说明沪铝期货和沪铜期货收益率序列分布的尾部较正态分布更厚，假定收益率序列服从正态分布是不合理的。

表3 沪铝GARCH(1，2)-GED模型估计结果

表4 沪铜GARCH(1，1)-GED模型估计结果

沪铝GARCH(1，2)-GED模型的条件方差估计值如图3所示。

沪铜GARCH(1，1)-GED模型的条件方差估计值如图4所示。

图3 沪铝GARCH(1，2)-GED模型的条件方差

根据GARCH模型的估计结果，我们就可以求出沪铝期货和沪铜期货市场风险的VaR值。

沪铝期货空头的VaR值为:

沪铝期货多头的VaR值为:

沪铜期货空头的VaR值为:

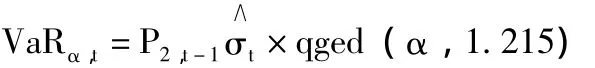
沪铜期货多头的VaR值为:

其中，qged(α，v)为自由度为v的GED分布在置信水平α下的分位数，σ∧t为条件方差的估计值。通过经计算可得:

由于GED分布是对称分布，所以，我们很容易得到:

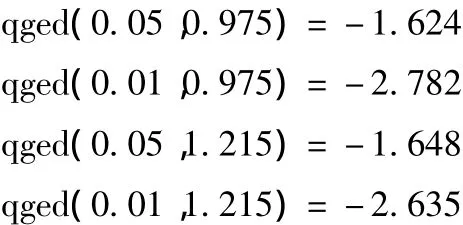
利用GARCH-GED模型估计的条件方差，可以求出沪铝期货和沪铜期货的VaR值。计算结果表明，在95%的置信水平下，沪铝期货和沪铜期货VaR值的均值分别为227.7元/吨和935.9元/吨;在99%的置信水平下，沪铝期货和沪铜期货VaR值的均值分别为264.1元/吨和1 215.3元/吨。

表5和表6分别给出了在95%的置信水平下，样本内沪铝期货和沪铜期货前十名VaR和条件方差的估计值及其对应的日期。

图4 沪铜GARCH(1，1)-GED模型的条件方差

表5 沪铝期货前十名VaR值和条件方差值

表5 沪铝期货前十名VaR值和条件方差值

VaR(元)日 期 σ2t 日 期1 157.7 2006-05-19 1.9E-06 2008-12-10 1 069.0 2006-05-23 1.7E-06 2008-12-11 988.1 2006-05-17 1.7E-06 2008-12-08 981.2 2006-05-25 1.7E-06 2008-10-20 975.7 2005-12-19 1.4E-06 2008-12-15 948.2 2006-02-08 1.4E-06 2009-04-17 940.8 2008-10-20 1.4E-06 2008-10-17 931.7 2006-05-24 1.3E-06 2008-10-13 898.7 2006-02-09 1.3E-06 2008-10-22 886.2 2006-05-12 1.3E-06 2008-12-16

表6 沪铜期货前十名VaR值和条件方差σ2t值

(三)基于Li［8］半参数方法的VaR估计

利用沪铝期货和沪铜期货收益率数据，根据Li［8］提出的半参数方法可以计算出收益率序列VaR的置信上限和下限，结果如表7所示。

表7 沪铝期货和沪铜期货基于半参数法的VaR估计值

(四)模型评价及测度结果分析

本文采用两种方法建立了沪铝期货和沪铜期货市场风险测量的VaR模型，可以通过反馈检验进行评价。在α=0.05条件下，分别用基于GARCH模型的方差—协方差法和半参数方法计算各自的VaR置信区间，再计算落入置信区间之外的观察值占总体的比率p，将p与α相比较，若p≤α，说明模型预测误差控制在5%之内，模型精度较好。计算结果表明，α=0.05时，两种方法落入区间之外的百分比全部小于5%。前一种方法该比率沪铝期货为0.049，沪铜期货为0.048;后一种方法该比率沪铝期货为0.038，沪铜期货为0.041。可见，两种模型的拟合效果都比较好。

从沪铝期货和沪铜期货市场风险测度的结果可以得出以下结论:(1)基于GARCH模型的估计结果表明，平均来看，沪铜期货的市场风险要高于沪铝期货。这一方面是因为铜的价格相对于铝的价格更高。剔除价格因素后，沪铜期货的市场风险仍然较沪铝期货更高，在95%的置信水平下沪铝期货和沪铜期货的VaR均值分别为0.014和0.024。半参数方法估计的结果同样表明，沪铝期货的市场风险相对于沪铜期货更低，在95%的置信水平下，沪铝期货和沪铜期货VaR的置信上限分别为0.017和0.026。(2)2006年5月份沪铝期货和沪铜期货的市场风险处于历史上的高位时期，而条件方差在2008年相对较高。

四、研究结论与建议

本文利用GARCH-GED模型和半参数方法对沪铝期货和沪铜期货的市场风险进行了测度，得出以下主要结论:(1)沪铝期货和沪铜期货收益率序列不服从正态分布，具有尖峰厚尾、波动聚集的现象。因此，基于正态分布假设的模型可能会对VaR产生错误的估计。 (2)基于GARCH-GED模型和半参数方法的估计结果均表明，沪铝期货的市场风险要低于沪铜期货的市场风险。上述结果对于相关企业进行套期保值准备，准确评估市场风险具有现实的指导意义。

随着中国经济的发展和工业化进程的不断推进，有色金属的产量和需求量都表现出快速增长的态势，其价格波动对有色金属行业和整个国民经济的影响越来越大。为了发挥期货市场规避现货价格波动风险的功能，上海期货交易所先后推出铜、铝、铅、锌等各种有色金属的期货合约。对于套期保值的投资者来说，有色金属的期货交易有效地规避了现货价格波动的风险。然而，期货价格波动又给他们带来了新的风险。对于非套期保值的投资者来说，期货价格的频繁波动使他们面临着巨大的风险。因此，理性的投资者应该选择在风险较小的时机入场，在风险较大的时机出场，并且在整个投资期间将最大的可能损失控制在自身能够承受的范围内。因此，有色金属期货价格波动风险的测度对于投资者的投资决策具有重要的参考价值，对于期货交易监管部门的监管以及期货交易所的风险管理和保证金比例的设定也具有重要的参考意义。

［1］韩德宗.基于VaR的我国商品期货市场风险的预警研究［J］.管理工程学报，2008，22(1):117-121.

［2］Jorion，P.Value at Risk，the New Benchmark for Controlling Derivatives Risks［M］.Mcgraw Hill，1997.

［3］Beltratti，A.，Morana，C.Computing Value at Risk with High Frequency Data ［J］.JournalofEmpirical Finance，1999，(6):431-455.

［4］丁岩，黄健.基于VaR模型的股指期货基差风险的研究［J］.经济论坛，2008，(10):110-111.

［5］张峭，王川，王克.我国畜产品市场价格风险度量与分析［J］.经济问题，2010，(3):90-94.

［6］叶青.基于GARCH和半参数法的VaR模型及其在中国股市风险分析中的应用［J］.统计研究，2000，(12):13-17.

［7］江涛.基于GARCH与半参数法VaR模型的证券市场风险的度量和分析:来自中国上海股票市场的经验证据［J］.金融研究，2010，(6):28-32.

［8］Li，D.X.Value at Risk Based on Volatility，Skewness and Kurotosis［EB/OL］.http://www.gloriamundi.org，1999.