利用面片法向均值滤波的混合型网格去噪方法

高 伟， 李 政， 康 倩

（天津凯发电气股份有限公司，天津 300384）

由于设备的准确度不够高或人为操作的误差，三维扫描仪获取的采样点拓扑重建得到的三角网格曲面难免会含有噪声，有效地去除这些噪声是对三角网格进行其它相关数字几何处理的前提。 去噪的目的就是在有效地去除噪声使网格曲面更加光滑的同时，保持网格原有的特征，而且不会产生体积的收缩和特征的扭曲等现象。目前已有了好多经典的网格去噪算法，可以根据不同标准对这些算法进行分类。比如，从时间复杂度考虑可以分为线性算法和非线性算法，可以分为迭代算法与非迭代算法。本文粗略地将以前的算法分为三类：各向同性的方法，各向异性的方法，混合型的方法。

各向同性的方法主要是基于 Laplacian算子的方法。标准的 Laplacian方法是将网格的顶点平移到其一环邻域顶点的重心，这种方法能够有效地去除噪声，但是会引起体积的收缩和特征的扭曲[1]。为了克服这些缺点好多学者提出了改进的方法[1-3]。另外，与以往局部的方法不同的是Ji[4]给出一种基于Laplacian算子的全局的保持特征的光顺去噪方法。

各向异性的方法，主要分为三种：基于曲率流和网格上偏微分方程(PDE)的方法[5-6]，基于面片法向平滑滤波的方法[7-10]，基于图像滤波器的方法。基于网格上曲率流和 PDE的方法的基本思想是将网格的去噪认为是网格随时间演化的过程，通过离散化微分方程逐步迭代得到理想的结果。面片法向平滑滤波的方法先平滑网格上的三角面片的法向量，再调整顶点的位置以逼近平滑后的法向量。另外，图像处理中的双边滤波器[11]和 Wiener滤波器[12]也相应地推广到了三角网格曲面上。

由于以上各种方法都有一定的使用范围，具有不同的优缺点。为此，将不同的方法加以整合的混合型去噪方法越来越受到重视，此类方法的目的是对不同方法进行组合，扬长避短，使其具有更好的性质和较强的鲁棒性[13-16]。

本文通过对已有的保持特征的面片均值滤波方法[8]的研究发现该种方法虽然具有不错的效果，但实验结果表明此方法不能有效地去除网格中含有的大噪声（图1 (d)）。为此本文提出了一种改进的混合型去噪方法Mean-Laplace，该方法继承了面片均值滤波方法保持特征的优点，但避免了其不能有效去除大噪声的缺点(图1(c))，具有较强的鲁棒性。

图1 各种去噪方法

本文的第1部分介绍了一些基本概念以及一些与本文相关的方法；第2部分介绍改进的保持特征的Mean-Laplace去噪方法；第3部分中对实验结果进行了比较和分析；最后在第4部分给出了结论以及以后的研究方向。

1 基本概念

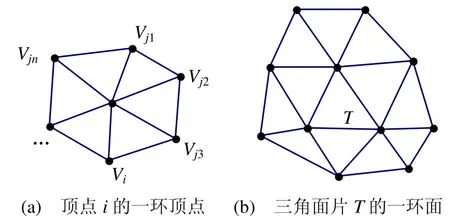
图2 一环顶点和一环面

网格上的噪声其实就是顶点偏离其正确位置的偏移量，偏移量的大小一定程度上刻画了噪声的大小。因而网格去噪的实质就是将网格上的顶点作一定的平移以尽可能地回到其正确的位置，即对于每一个顶点i有

其中 Vi为顶点i的原来坐标，为顶点i的平移向量，为顶点i平移后的坐标。因此，去噪过程的实质就是求每一顶点的平移量。下面介绍与本文相关的两种去噪方法。

1.1 Laplacian方法

Laplacian方法[1]中每个顶点i的平移向量等于伞状算子在该点的作用D( Vi)，其中

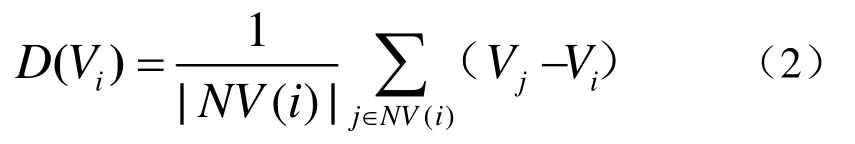
NV( i)为顶点i的一环顶点的集合，|NV( i)|为集合NV( i)中元素的个数。Laplacian方法是一种经典的去噪方法，其实是一低通滤波器。该方法能够有效地去除网格中含有的大小噪声，但是随着迭代次数的增加会去除一些网格上高频的特征，从而产生网格特征的扭曲以及体积的收缩[1]。为此，已提出了好多相应的改进方法[2-4]。

1.2 面片法向均值滤波

面片法向均值滤波[8]就是先将每个三角面片的法向量用其一环面的法向量的加权平均值去更新，再调整顶点的位置去逼近更新后的法向量。此时顶点i的平移向量记为 M ean( Vi)

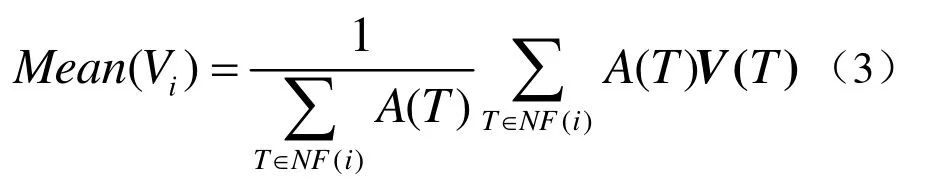
其中 NF( i)为顶点i的一环面的集合，A( T)为三角面片T的面积，V(T)一个投影向量，计算公式如下

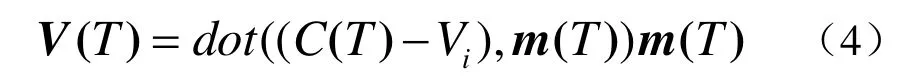
C( T)为三角面片T的重心的坐标, m(T)为面片T的更新后的法向量，法向量的更新公式为

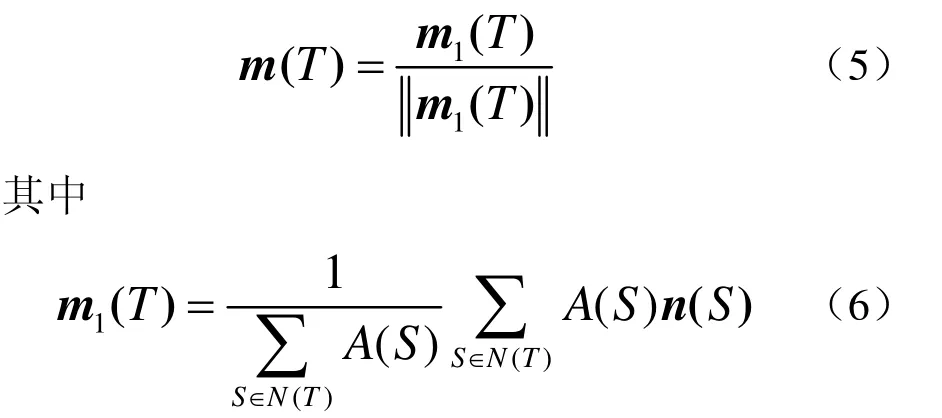
N( T ) 为三角面片T的一环面的集合，n(S)为三角面片S原来的法向量，A( S)为三角面片S的面积。这种方法先平滑网格上的一阶信息法向量，再调整顶点的位置去逼近平滑后的法向量，能够有效地保持网格原有的特征。但是，对于大噪声网格，这种方法会将噪声当作特征而保留下来，会产生去噪不彻底的效果，不能有效地去除大噪声。

2 改进的Mean-Laplace方法

1.2节中介绍的面片法向均值滤波的方法对含有一定特征但是特征不很丰富的网格进行去噪有很好的效果[8]，但是通过实验发现该方法不能够有效地去除网格上的大噪声。原因是该方法不能区分噪声顶点和一般顶点，从而将噪声当作特征保持下来，产生了去噪不彻底的问题。借鉴以前学者区分噪声和特征的思想[13,15]，本文根据顶点的一环正常边的二面角的平均值将顶点分为噪声顶点和一般顶点，把平均值小于一定阈值的顶点认为噪声顶点，其余点为一般顶点。噪声顶点的平移向量为 Laplacian的平移向量，一般顶点的平移向量为面片法向均值滤波方法中的平移向量。该方法是迭代方法, 需要一个二面角阈值的参数θ，每一次迭代具体步骤如下：

第一步 计算顶点i的一环正常边的平均二面角iθ

第二步 根据θi决定顶点i的平移向量

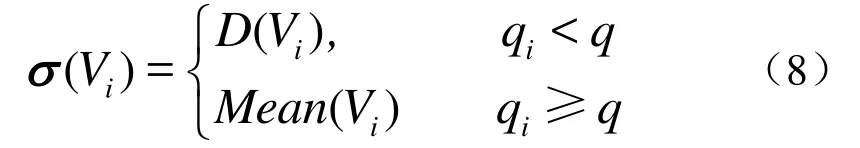
D( Vi) ， M ean( Vi) 如式(2)、式(3)所示。

第三步 更新每一个顶点位置，公式如下

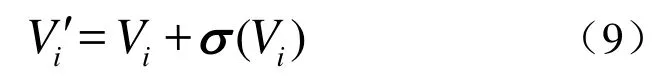
3 实验结果与分析

为了验证Mean-Laplace方法的有效性，采用向无噪声网格中加入噪声，然后进行去噪，再与原网格比较的方法。由于现实中噪声可以认为服从高斯分布，本文中加入的噪声均服从均值为零的高斯分布，而方差的大小在一定程度上衡量了噪声的大小。可认为，方差低于网格平均边长的50%的噪声称为小噪声，介于 50%与 100%之间的为大噪声，大于100%的则为超大噪声。

首先，验证本文的方法对大小噪声的有效性， 采用向同一网格添加不同方差的噪声，然后去噪进行比较的方法。由图3和图1发现随着噪声的不断增大，面片均值滤波方法不能有效地去除大噪声。然而，本文提出的 Mean-Laplace方法对于大小噪声网格均有较好的去噪效果。从中可以看出 Mean-Laplace方法是对面片均值滤波的一种很好的改进，对于小噪声它们的去噪效果几乎没有差别，但对于大噪声，本文的方法具有明显的优越性。在实验中，二面角阈值一般取在120º左右，当然，如果想进一步保持特征，则阈值应要小些，一般为90º左右。相反，如果想得到较光滑的效果，取值在150º左右效果不错。两种极端情况，如阈值为0则本方法退化为面片均值滤波，若阈值为180º则退化为Laplacian方法。

图3 不同程度噪声的去噪结果比较，从上到下依次为噪声网格，本文方法去噪结果，面片均值滤波结果

其次，为了进一步分析实验结果。作者分析了去噪后的网格的体积[2]和所有三角面片的面积和相对于原来无噪声网格的百分比。另外，引入了以下的距离误差与法向误差来衡量去噪后网格相对与原来无噪声网格的变化的大小，误差越小一定意义上表明去噪效果越好[8,15]。设原来无噪声网格为 M ={ V, E, F}，去噪后网格为M ′ ={ V ′, E ′, F ′}，距离误差εv与法向误差εn分别为

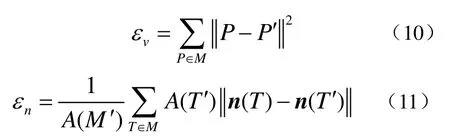
表1分析了图1、图3中向小猪网格中加入不同程度噪声，进行去噪后的误差分析，从中可以看出本文的方法是对面片法向均值滤波去噪方法的一种有效的改进。

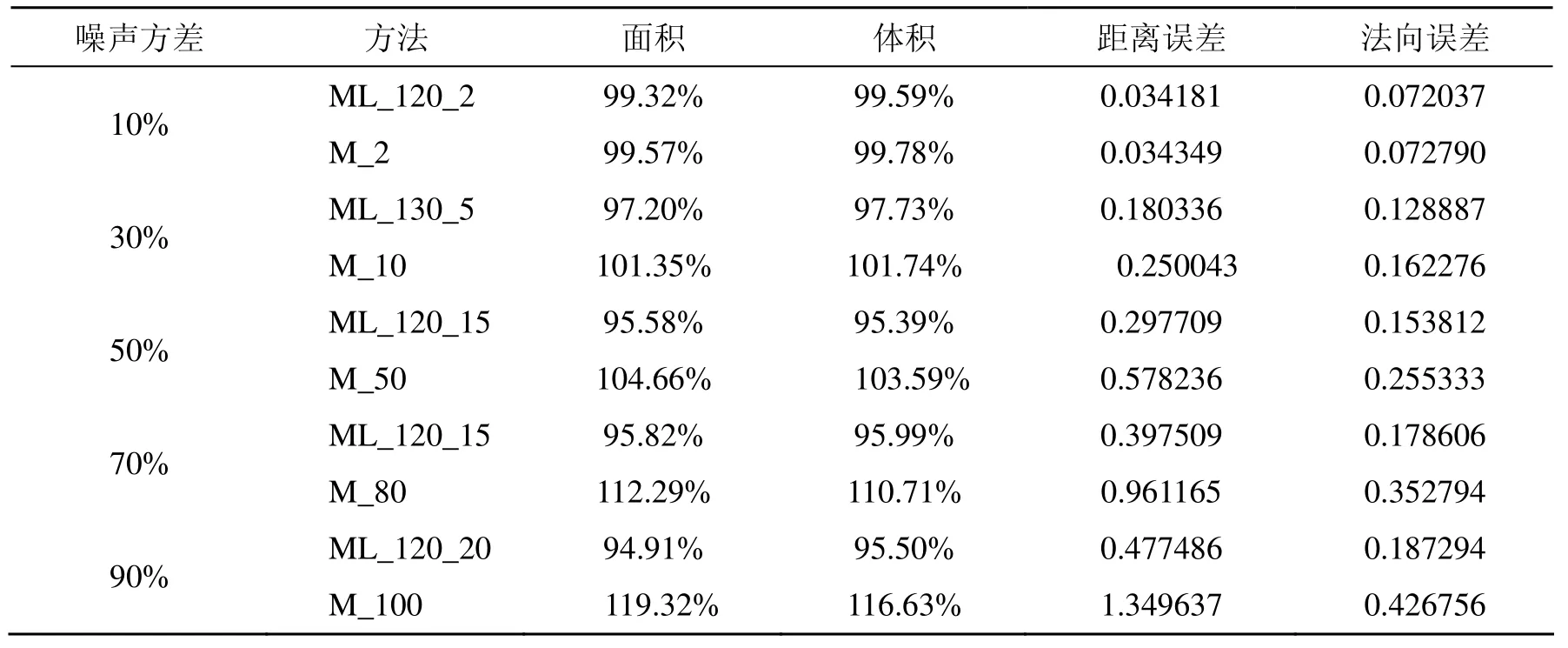
表1 图1图3中加入不同程度噪声，进行去噪后的误差分析

最后，通过去除一个由重建得到的含有噪声的网格说明本文提出的方法有不错的效果。图4是用不同方法对一重建得到网格的去噪结果，从中可以看出本文的方法去噪比较有效，并且能够保持网格的特征。

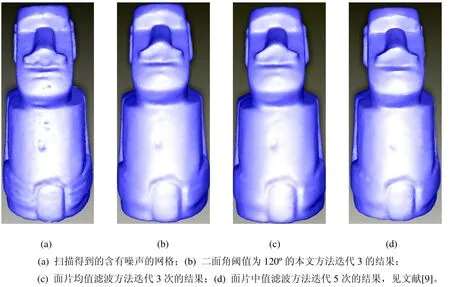
图4 用不同方法对一重建得到网格的去噪结果

4 结 论

鉴于面片法向均值滤波方法不能有效去除网格上大噪声的缺点，本文提出了一种基于顶点分类的改进的混合型去噪方法。理论和实验表明，本文提出的方法不仅克服了面片法向均值滤波方法不能去除大噪声的缺点，而且继承了其保持网格特征的优点。本文提出的方法具有较强的鲁棒性，对含有一定特征但是特征不是很丰富的网格的去噪有很好的效果。但是，此方法中二面角阈值的选取不够自适应，希望下一步能够给出一种自适应的方法。并且，本方法不能保持网格尖锐的特征，这也是以后要努力解决的问题。

[1]Taubin G. A signal processing approach to fair surface design [C]//SIGGRAPH 1995, 1995: 351-358.

[2]Desbrun M, Meyer M, Schroder P, et al. Implicit fairing of irregular meshes using diffusion and curvature flow [C]//SIGGRAPH 99, 1999: 317-324.

[3]Liu X G, Bao H J, Shum H Y, et al. A novel volume constrained smoothing method for meshes [J].Graphics Models, 2002, 64(3-4): 169-182.

[4]Ji Z P, Liu L G, Wang G J. A global laplacian smoothing approach with feature preservation [C]//Ninth International Conference on Computer Aided Design and Computer Graphics (CAD/CG 2005),2005: 269-274.

[5]Meyer M, Desbrun M, Schroder P, et al. Discrete differential geometry operators for triangulated 2-manifolds [C]//Proceedings of Visualization and Mathematics, 2002: 35-57.

[6]Zhang Y, Ben Hamza A. Vertex-based diffusion for 3-D mesh denoising [J]. IEEE Transactions on Image Processing, 2007, 16(4): 1036-1045.

[7]Taubin G. Linear anisotropic mesh filters [R]. IBM Research Technical Report RC-22213, 2001.

[8]Yagou H, Ohtake Y, Belyaev A. Mesh smoothing via mean and median filtering applied to face normals [C]//Proc. Geometric Modeling and Processing, 2002:124-131.

[9]Yagou H, Belyaev A, Wei D. Mesh median filter for smoothing 3-D polygonal surface [C]//Cyber Worlds 2002, Tokyo, Japan, 2002: 6-8.

[10]Sun X F, Paul L Rosin, Ralph R Martin, et al. Random walks for feature-preserving mesh denoising [J].Computer Aided Geometric Design, 2008, 25(7):437-456.

[11]Fleishman S, Drori I, Cohen-Or D. Bilateral mesh denoising [C]//Proc. ACM SIGGRAPH 2003, 2003:950-953.

[12]Alexa M. Wiener filtering of meshes [C]//Proceedings of Shape Modeling International, 2002: 51-57.

[13]胡国飞, 彭生群. 基于顶点预测的特征保持网格光顺算法[J]. 浙江大学学报(工学版), 2004, 38(12):1535-1539.

[14]Shen J, Maxim B, Akingbehin K. Accurate correction of surface noises of polygonal meshes [J]. Int. J.Numer. Meth. Engng, 2005, 64: 1678-1698.

[15]杨长春, 倪彤光. 一种高效的混合曲面光顺算法[J].计算机应用, 2005, 25(11): 2609-2611.

[16]Chen C Y, Cheng K Y. A direction-oriented sharpness dependent filter for 3D polygon meshes [J].Computers & Graphics, 2008, 32: 129-140.