试析启发式教学及其在工程图学课程中的贯彻
毛 昕, 黄 英, 那履弘, 刘 阳
(东北大学机械工程与自动化学院,辽宁 沈阳 110004)
启发式教学是一项教学原则,它体现了通过教学活动培养人的思维、能力与素质的本质要求和内在特点,是在各个教学环节中都应该遵循的基本要求。启发式教学一词对于教师非但并不陌生,且耳熟能详,但究竟什么是启发式教学、怎样启发却常常感到难以把握。因此,有必要对启发式教学及其在课程中的有效贯彻进行剖析,以便更好地发挥启发式教学的作用,提高人才的培养质量。
1 什么是启发式教学
1.1 启发式教学的历史溯源
在中国历史上,“启发”一词最早出于孔子的《论语·述而》,孔子说:“不愤不启,不悱不发。举一隅不以三隅反,则不复也。”意思是说,只有在学生对某一问题积极思考而又未能搞通时教师才给予指导,当学生想说又难于表达时教师才加以引发,帮助其用准确的语言表达出来;教师在讲清一个问题之后,如果学生不能由此及彼,推知其他相同问题的解法,教师就不必再往下教。这里前一层意思是说启发要适时,后一层意思则是说启发要适度。孔子以后,战国晚期的教育教学专著《学记》中又提出“道而弗牵,强而弗抑,开而弗达”,意思是说要引导学生而不是硬拖着学生走,严格要求学生但不施加压力,启发学生而不是代替学生达成结论。
在西方,启发式教学可以追溯到古希腊哲学家苏格拉底的“产婆术”。这种方法主要采用一问一答的方式与学生探讨问题,他首先提出问题请教学生,当学生回答后,他就指出答案中的矛盾,引导学生重新思考并给出新的答案,接着他又指出新答案中的矛盾,迫使学生再行思考和回答,通过这种追问的方式,直到学生得出满意的答案为止。这些答案是在教师不断启发下,通过学生的主动思考来获得的。
孔子与苏格拉底的启发式教学有着许多共同之处。首先,《论语》和古希腊哲学家柏拉图的《理想国》提供了孔子与苏格拉底的教学大都采用谈话、问答的方式,教师与学生间有着密切的思想交流。其次,他们都把学生放在教学中的主体地位。孔子强调教学中学生的积极性,要顺势而为;苏格拉底则从不把自己看作是一个智者,只是作为参与者在教学中与学生一起探讨,尊重学生的个人观点,通过递进的辨析来增强对真理的认知。再次,他们都认为教学要想得到有效的效果,必须是一个引导而非灌输的过程,学生要感受到学习的需求和欲望,同时面临一定的不解和困惑,才能更好地发掘思维的潜力和能动,提高学习的质量。
孔子与苏格拉底的启发式教学也有着很大的区别。其根本之处在于,孔子的教育主要解决学生“应当如何……”的问题,是道德伦理的教育,关注的是在现实生活中怎样妥善处理问题,是圣贤的教育。而苏格拉底的教育主要解决学生“什么是……”的问题,其目的在于追问事物的本质和真理,是哲学和哲学家的教育[1]。两种教育目标取向的不同,造成了他们启发式教学中一些方式的不同,但尽管如此,对于各自教育目的的实现来说,它们都是卓有成效的,都是启发式教学的宝贵财富。
1.2 启发式教学的现代思考
今天的教学,从教学目的、教学环境到教学内容都发生了质的变化。学习首先成为一种基于知识传递的科学与技术的教育,与历史上哲学与道德的教育相比,它可以以简单和直接得多的方式传达给学生;另外,今天的教育已是一种规模化的大众教育,教和学都受到相应规范的约束与控制,那种自由、闲散的教学环境已经不在。尽管我们不可能、也不应该在今天的教学中简单复制孔子与苏格拉底的启发式教学方式,但几千年来古典启发式教学中仍然有它不曾改变的东西影响至今,比如教学中对道德的关注和对本质的追求、对学习者主体地位的依托以及在策略上对困境的恰当设置等。
在基于知识传递的科技教育环境下,启发式教学的目标更多地体现在两个方面。一是有效学习,强调人对知识的掌握不是一个被动的接受过程,而是在外部刺激下对知识信息分析、处理和构建的一个内省的过程,学习者的内因动力越强,头脑中信息处理能力越强,学习的效果越好,效率越高。二是自主学习,强调对知识需求的主动把握和知识信息的独立分析和掌握。因此,与古代的启发式教学相比,现代启发式教学在实践中更多地体现出方法和手段的特点,其重心也不再是启发学习者去对世界本源和社会秩序的把握,而是放在启发和培养人的思维能力方面。
由上面的分析可见,现代启发式教学的内涵是指教师在教学中依据教学的客观规律,重视学生感知、 记忆、 思维、 兴趣、 动机等智力因素和非智力因素,有效地调动学生的内在认知需求,激发学生的学习动机,使学生的思维和智力活动处于积极状态,自觉、独立地开展思维,融会贯通地掌握知识和技能,并形成可持续发展的学习能力。
2 启发式教学的基本模式
教师在教学中是否有效地进行启发式教学,唯一的判断标准应该是看其教学对象—— 学生是否受到了启发。关于“启发”一词,现代汉语词典的解释是:阐明事例,引起对方联想而有所领悟。其中的三个关键词是“事例”、“联想”和“领悟”,这里的“事例”是广义的,是一种情境,它可能是一个问题,一次实验或一个故事等等。“事例”是起点,“领悟”是目的,而“联想”则是手段。
那么,能引发联想继而有所领悟的事例有什么共同特点呢? 下面略举几例:
【事例1】这是前苏联著名教育家苏霍姆林斯基记录的一件真事:校园的花房里开出了一朵硕大的玫瑰花,全校师生非常惊讶,每天都有许多师生来观看,有一天他在校园里散步,看到幼儿园的一个 4岁女孩在花房里摘下了那朵玫瑰花,从容地往外走。他弯下腰亲切地问:“孩子,你为什么要摘这朵花?能告诉我吗?”小女孩害羞地说:“奶奶病得很重,我告诉她学校里有这样一朵大玫瑰花,奶奶有点不信,我现在摘下来送给她看,看过后我就把花送回来。”听了孩子天真的回答,苏霍姆林斯基的心颤动了,他搀着小女孩,在花房里又摘下两朵大玫瑰花,对孩子说:“这一朵是奖给你的,你是一个懂得爱的孩子;这一朵是送给妈妈的,感谢她养育了你这样的好孩子”[2]。
一位老师被这种爱的教育深深感动并突发想象,让学生用故事的前半段续写一篇作文。结果令他大失所望,几百个学生文章的核心内容都是写教育家如何教育小女孩不要损害公物,对缺乏公德教育的忧心忡忡,甚至对小女孩做出处罚……。
这件事给这位老师,也给读者很强的震撼,使人联想到的显然不止是学生看上去对道德规范的知守,更多地是语文教学饱受诟病的呆板,思维的僵化,甚至是说教式教育和应试教育带来的对人性美感悟的淡漠和同情、怜悯之心的缺失……,从而产生“教育急需完善”的领悟。
【事例2】问题:以“体”为主,削减画法几何教学内容是制图课程教学改革的成果吗?
这个问题会让人产生多方面的联想,比如削减画法几何内容是我们所追求的吗?削减以保证“体”的教学,是主动还是被动的?画法几何对“体”的学习用处不大吗?画法几何对人的思维训练究竟有多大的作用?数字化环境下画法几何没有应用价值了吗……?
这是一个有些发散的问题,不同的思考可能形成不同的领悟,但对于制图教师来说,引发联想是肯定的。
【事例3】不可展曲面近似展开的误差分析中的启示。
对于规则不可展曲面Σ,沿其上任意曲线Γ,存在一个可展曲面Σ1与Σ相切。近似展开时,先在局部范围内将Σ映射至Σ1,再对Σ1进行展开。分别对球面和环面进行操作(取Γ为母线,这时Σ1为柱面),得出的相对面积误差和相对纬线长度误差均为(u为Γ对应的参数0值),在这种共性提示下,联想到对一般回转曲面进行分析,得出了相同的结论。于是得出一般规律:回转曲面柱面置换法近似展开时,相对纬线长度误差与其纬度无关,且与相对面积误差等值[3]。
尽管上面三个事例内容完全不同,但都引发了联想并有所领悟,即形成了启发。引发联想的因素主要有两个:一是价值性。有价值才引起关注,当然这是对被启发的个体而言,比如例1能引起大多数人的关注,例2会引起制图教师的关注,而例3就只能引起具体研究者的关注了;二是缺憾性。“缺”让人感到“没有”,“憾”让人感到“该有”,比如例 1中人文教育上的缺憾,例2中对教改认识上的缺憾和例3中对一般规律求而未得的缺憾。在关注基础上,缺憾引发探求和补缺的欲望和空间。可见,启发过程中,价值性是前提,缺憾性是动因。于是,启发式教学可基本概括为图1所示的模式。

图1 启发式教学的基本模式
3 启发式教学的理论依据和基本策略
3.1 启发式教学的理论依据
首先,启发式教学符合建构主义的教学理论,即在学习过程中,学习者不是外部刺激的被动接受者,而是头脑中知识信息的主动建构者。学习者以自己已有的知识经验为基础,通过与外界的相互作用,对新知识信息进行加工处理,并对自己原有的经验进行改造和重组,以形成新的知识结构。这个过程只能由学习者主动完成,而不能由其他人替代。其次,外因通过内因而起作用的辩证唯物主义原理为启发式教学提供了哲学依据。另外,从心理学的角度,出于对实用、审美和文化等方面的需求,人总有一种追求规则性的心里取向,即对规律、均衡、完整、完美等的追求。启发式教学中价值性和缺憾性情境的呈现恰好对这种心理形成诱发,这构成了启发式教学的心理学依据[4]。
3.2 启发式教学的基本策略
教学中怎样才能形成启发?从上面的分析可见,要使学生受到启发,产生联想并有所领悟,需要价值性和缺憾性情境的刺激和驱动,“思维永远从问题开始”,因而需要教师对这种情境或问题加以设计,即启发式教学的基本策略是教师对有价值的缺憾性情境或问题的恰当设计与呈现。
那么怎样让学生感到“缺”和“憾”呢?
“缺”是启发式教学的逻辑起点,有了“缺”才可能引起“憾”。“缺”与“不缺”是对立统一的两个方面,“缺”是相对于“不缺”而言,没有“不缺”就谈不上“缺”,因此在设计“缺”时,首先要先设计所谓的“不缺”,即启发的已知条件。好的已知条件一是要与学生现有的知识、经验、兴趣、经历相联系,联系越紧密,思维越容易被触发;二是要进行恰当的组织,组织得越好,“缺”越容易被衬托出来。已知条件的组织可以采用语言、文字、图式等不同的形式,图2和图3是图式形式的简单举例。图2中用直角三角形法求一般位置直线AB实长和倾角的图式结构,右下侧的分支一般不讲,空白处形成“缺”,受“不缺”的启发,容易看出应分别为△XAB和 a″b″;图3是几何对象从属关系的图式结构,最外层结构应表示“体”。从属性是画法几何的不变性质之一,线上取点、和面上取点、线是画法几何的基本作图,而体上取面则是线面分析法读图的基础。

图2 求一般位置直线的实长和倾角
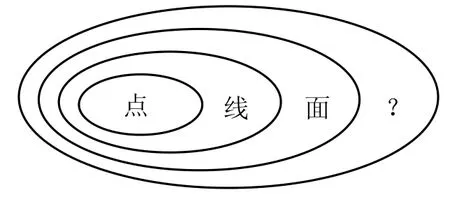
图3 几何对象的从属关系
“憾”是感觉不应该缺,因而产生补缺的意愿,引发思考。这在缺憾性情境或问题设置中,一是要让学生感到有所需求,值得“憾”;二是要让学生感到有“补缺”(通过思考能有所领悟)的可能性。后者主要取决于“缺”的程度,缺的太少,联想的空间不足,启发的效果不够;缺的太多,启发条件不够,或使联想难于产生,或使人感觉补缺的可能性不大,意愿受到抑制。因此,要恰当设置“缺”的程度,使学生要“跳一跳”,才能且能够“摸得着”。
4 启发式教学在工程图学课程中的贯彻
4.1 启发的主要方向
(1)结合画法几何理论的启发 在工程图学课程中,画法几何理论占有重要地位。教学中可结合画法几何的起源和历史、投影法的基本思想、内容间的逻辑关系、联系与区别和解题方法等方面进行启发,提高学生几何分析与求解方面的能力。
(2)结合思维训练方面的启发 工程图学以形象思维作为课程学习的主要思维方式,思维能力培养也是课程重要的教学任务和培养目标。而启发式教学中,学生在缺憾性情境诱导下引发联想并有所领悟,联想和想象思维是其中的重要环节。可见,课程本身与启发式教学在思维能力培养上形成有效的契合,启发式教学与课程教学任务和目标相辅相成,互相促进。教学中可结合思维理论、图形的表达和理解、解题的思维方法和步骤、形象思维与逻辑思维的综合运用和协调发展(如解画法几何综合题时要确定所需的空间概念和应用顺序,前者多为形象思维,后者多为逻辑思维)乃至一些具体的训练方法来进行启发。这有助于学生既领悟到了启发的结果,又锻炼了思维;有助于引领学生由教师启发向自我启发转变,学会学习,这也是启发式教学追寻的根本目标。
(3)结合工程实际的启发 工程图学是学生最先接触到工程实际的课程,这既为教学带来难度,也为启发式教学带来更多的机会和更广阔的空间。教学中,在工程问题的几何建模、标准化的概念和应用、工程设计与制造初步和工作作风培养等方面,都可以作为素材形成生动的启发情境,进行启发式教学。
(4)结合图学观形成的启发 图学观是对图学整体上的认识。图具有形象性、并行性和多属性的特点,因而在对客观事物表达和交流思想方面有着自身的优势。今天,图除了作为表达交流工具外,也是科学研究的基本手段和科学思维的重要形式之一,因而学生图学观念和素养的培养是很重要的。教学中可在图学的认知观、价值观、哲学观、审美观及方法论等诸方面进行适当、有益的启发,以利于学生认知结构甚至世界观的完善和发展。
4.2 启发的层次
启发式教学可根据启发的效果分为不同的层次。
(1)浅层次启发 指通过启发使学生达到对某一具体知识的掌握。启发的情境较简单,引发的联想环节较少,领悟较具体。比如点的投影中讲到点的投影和坐标的关系,学生容易理解点的一个投影确定点的两个坐标,点的两个坐标也唯一确定一个投影。如提问:给出点的一个坐标确定了什么?学生起初可能觉得什么也没确定,若提示轨迹概念,学生能想到它确定了一个平行于投影面的平面;再引申:给出点的两个坐标呢?结论是确定两个平行于投影面的平面。而两个平面相交于直线,由此领悟到:点的两个坐标确定其一个投影,而这个投影表示了垂直于该投影面的一条直线。
(2)深层次启发 指通过启发使学生不仅掌握某一具体知识,而且在思想方法上有所领悟。这时启发的情境较复杂,引发的联想环节较多,领悟较丰富和深刻。比如继续上面的问题:由点的投影和坐标间的关系,你想到了什么?产生的联想会丰富得多。首先,点的投影和点的坐标都可以确定点的空间位置,当两种不同方法解决了同一个问题,两种方法之间可能存在某种内在联系(投影与坐标的互换);当两个问题可以用同一个方法解决时,两种问题之间也可能存在某种内在联系,由此可产生方法论层面的领悟。此外,投影属空间形式,坐标属数量关系,它们间的关系体现了“形”与“数”的结合与转换。可让学生回顾自己涉及形数结合的经验,如函数图像、集合问题、矢量表达等,若进一步展开,可简介数学上形数结合的典范,即解析几何(代数与几何)和微分几何(分析与几何)。由此学生又可形成形数结合思想和数学史层面的领悟。
4.3 启发的常用形式
(1)结构启发 事物的相关部分往往按照一定的搭配和排列形成某种结构。当这种结构在某处出现空缺时,就造成结构的不平衡,容易引起注意和补缺的意愿。图4和图5是图式结构的两个例子。
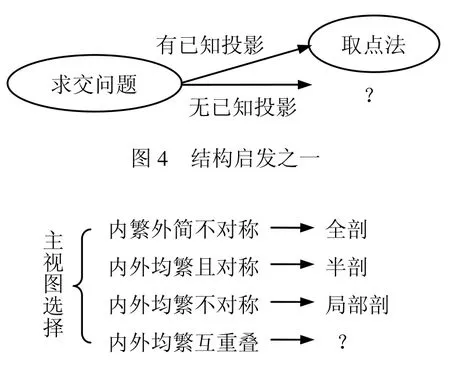
图5 结构启发之二
(2)问题启发 通过提出问题进行启发。比如:图6中(a)、(b)两图有什么不同?这是一个简单的问题,学生能够答出(b)图中X方向没有定位。进一步还可提问:(b)图什么情况下可用(在问题与X方向位置无关时)?怎样使X方向定位(加原点)?原点加在何处(理论上可加在X轴任意位置;应用上应考虑方便)?另外,(a)图中A点的轨迹是一条正垂线,(b)图中随O点的位置不同,A点的轨迹是一个水平面。可见,问题虽小,也能形成应用层面和问题相对性层面的启发。

图6 问题启发
(3)引论启发 广义地指在把新知识讲授给学生时所进行的的铺垫和引导,主要包括温故式启发和概貌性启发。温故式启发是说在学习新知识时,要尽量与学生先前已有的知识和经验建立起联系,既使学生的知识结构得到自然的延伸,又容易吸引学生对新知识的渴望。概貌性启发是说在新知识详细讲授之前,要提供给学生一组具有概括性和组织性的框架信息,使其大概了解新知识在整体知识系统中的位置和分量,便于新知识在头脑中的归档,这就像拼图游戏时,有整幅图画的引导就会方便得多一样。
(4)应用启发 指通过所学知识的应用使学生受到启发。“学到用时方恨少”,除了习题、作业之外,应注重结合工程实际的应用,多用好于少用,早用好于晚用。有条件可组织学生先感受生产实践,再进行课堂教学,以便“带着问题学”,提高学习效果。同时教学改革中对图学实验和研究式学习方式的探索也是很有益的。
(5)事件启发 指运用所发生事件的真实性和影响力来达到对学生的启发。特别是课程中一些“叙述性”内容,有些虽很重要,但常规讲授往往不易引起注意,比如标准化、工作作风等,这时不妨改变一下思路,采用事件启发往往会给学生带来更深刻、持久的印象和领悟。
(6)趣味启发 趣味性情境或问题容易激发学生学习、探讨的积极性,对所受启发印象更加长久,同时也是愉快教学有效的助推剂。图7中的两个立体要补画左视图,已知视图的规则性会引起兴趣,其中(b)图不很简单,看懂后会得到“类似形不一定是同一平面的对应投影”的一般性领悟。图8是三等径正交圆柱体公共部分的形状和投影,它由十二块(每个圆柱面四块)菱形柱面片围成,柱面间交于十二条椭圆弧相贯线。沿轴向的三个视图形状相同,外轮廓分别是三个圆柱面的投影,相贯线积聚为直线。分析过程中可得到“各要素地位相同,因而各向同性”等一般性领悟。图9是要在右边三个立体中找出一个与左侧立体形状相同的立体,虽不很难,但是一个“心理旋转”的思维过程,这可引申到认知心理学关于表象加工非常重要的一项实验研究——心理旋转实验。

图7 补画立体的左视图
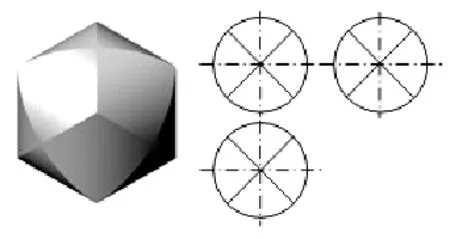
图8 等径正交三圆柱的交集及其投影
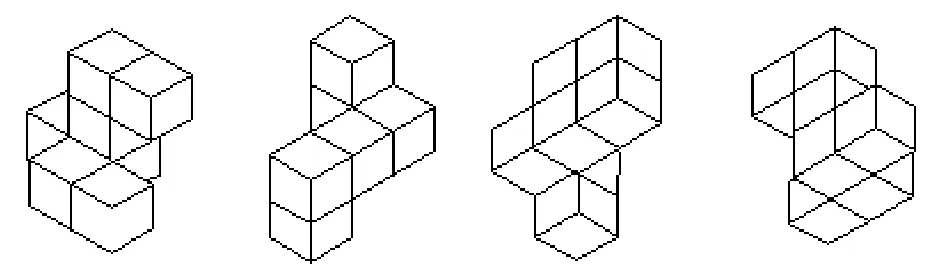
图9 哪一个与左边立体形状相同
5 结束语
启发式教学是在教师引导下,通过有价值的缺憾性情境或问题的恰当设置,引发学生的联想并使其得到领悟。启发式教学能够启迪学生的思想,促进思维,不仅提高教学质量,而且有利于学生的持续发展。启发式教学作为一项教学原则,应在课程的各个教学环节中加以重视和贯彻,并使其成为教学系统中一种常态的、自然的工作方式。启发式教学贯彻的关键在于教师自身的业务修养,要使启发深刻,首先教师自己要对课程有深刻的理解,要站在课程之上来把握教学,这也是反映教师教学能力的最重要方面。
[1]周兴国. “启发式”教学的“中外”与“古今”[J]. 华东师范大学学报, 2008, 26(2): 10-15.
[2]吴 非. 不跪着教书[M]. 上海: 华东师范大学出版社, 2005. 3-4.
[3]毛 昕, 侯 悦. 不可展回转曲面近似展开的精度分析[J]. 工程图学学报, 1998, 19(4): 1-9.
[4]张忠华, 周 阳. 对启发式教学几个问题的探索[J].教育学刊, 2009, (2): 50-52.

