考虑暂态电压稳定的二级电压紧急控制*
刘明波 高强 林舜江 潮铸
(华南理工大学电力学院∥广东省绿色能源技术重点实验室,广东广州510640)
暂态电压稳定问题又称为短期电压稳定问题,主要是由具有快速调节特性的负荷引起[1],电动机负荷是电力系统中最主要的动态负荷,由于系统故障引起了系统中负荷母线的电压跌落,负荷中的感应电动机在电压下降条件下吸收的有功先减小后不断地恢复,吸收的无功不断增大;感应电动机在其端电压低于某限定值下会发生堵转并从电网吸收大量的无功,这些快速动态特性造成了系统中一些母线出现暂态电压失稳[2-5].
目前的暂态电压稳定控制手段主要分为预防控制和紧急控制,文献[6]中构造了暂态电压安全预防控制优化模型,通过对电网分区后进行优化计算,调节各分区内节点无功注入来全面保证系统暂态电压稳定.文献[7]中则采用轨迹灵敏度法求解暂态电压稳定的预防控制优化问题;紧急控制的主要方式有快速切除故障元件和低压切负荷.文献[8]中针对包含单感应电动机负荷的无穷大母线系统提出了暂态电压稳定极限切除时间的概念.文献[9]在文献[8]的基础上做了进一步研究,认为当系统发生短路时,如果故障切除时间大于某一极限时间,则系统将失去电压稳定,这一极限时间称为系统保持暂态电压稳定的故障极限切除时间.文献[10]中定量分析了低压切负荷的暂态电压紧急控制措施.
二级电压控制是一种区域控制,主要目的是保证中枢母线电压等于三级电压控制下发的设定值,如果中枢母线的电压幅值产生偏差,二级电压控制器则按照预定的控制规律改变一级电压控制器的设定参考值.正常模式下二级电压控制的时间常数为几十秒到分钟级,文中取50s,显然这种正常的控制模式在系统发生大扰动后的暂态过程中来不及动作.
文中提出应对系统突发大扰动情况下的暂态电压稳定问题的二级电压紧急控制策略,并在PSAT(Power System Analysis Toolbox)仿真环境下建立含二级电压控制和一级电压控制的电力系统暂态电压稳定仿真模型[11],通过新英格兰 39节点系统在两个故障情况下实施二级电压紧急控制保持暂态电压稳定的算例,从而验证所提出控制模型和策略的正确性和有效性.
1 暂态电压稳定分析的数学模型
电力系统的暂态电压稳定的动态过程可用如下微分代数方程组描述:

式中:x为系统状态变量;y为母线电压;f、g分别为向量函数.
式(1)为描述系统各元件动态的微分方程,包括对暂态电压稳定起重要作用的发电机及其励磁系统的动态和负荷的动态.
发电机采用四阶实用模型[12],状态方程如下:

式中:E'q、E'd分别为发电机的横轴和纵轴暂态电势;T'd0、T'q0分别为d轴和q轴开路暂态时间常数;Ef为励磁电压;Xd、X'd分别为d轴电抗和暂态电抗;Xq、X'q分别为q轴电抗和暂态电抗;δ和ω为发电机功角和角速度;Pm为机械功率;ra为定子各相绕组的电阻;ωB为角速度基值;M为发电机的转子运动惯性时间常数;ud、uq分别为发电机d、q轴电压;id和iq可由下式求出:

式中,Ugd和Ugq表达式如下:

励磁系统采用文献[12]的三阶模型,如图1所示.
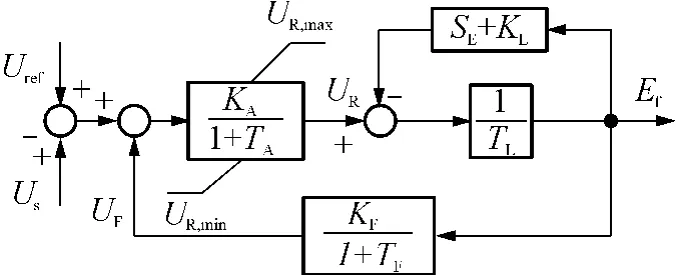
图1 励磁系统框图Fig.1 Block diagram of excitation system
图1中,UR为励磁机励磁电压;Uref为发电机端电压设定值;Ut、Us为输入电压参数;KA、TA分别为惯性放大环节的放大倍数和时间常数;SE为饱和系数;KL为自并励系数;TL为励磁机时间常数;Ef为发电机励磁电压;KF、TF分别为为励磁负反馈环节的放大倍数和时间常数;UF为励磁负反馈电压.
励磁系统的状态方程如下:
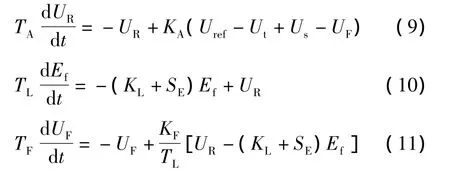
负荷则采用文献[13]中的三阶机电暂态感应电动机并联恒阻抗模型,该模型广泛应用在我国多个区域或省级电网调度中心的日常暂态稳定计算中,其状态方程如下:
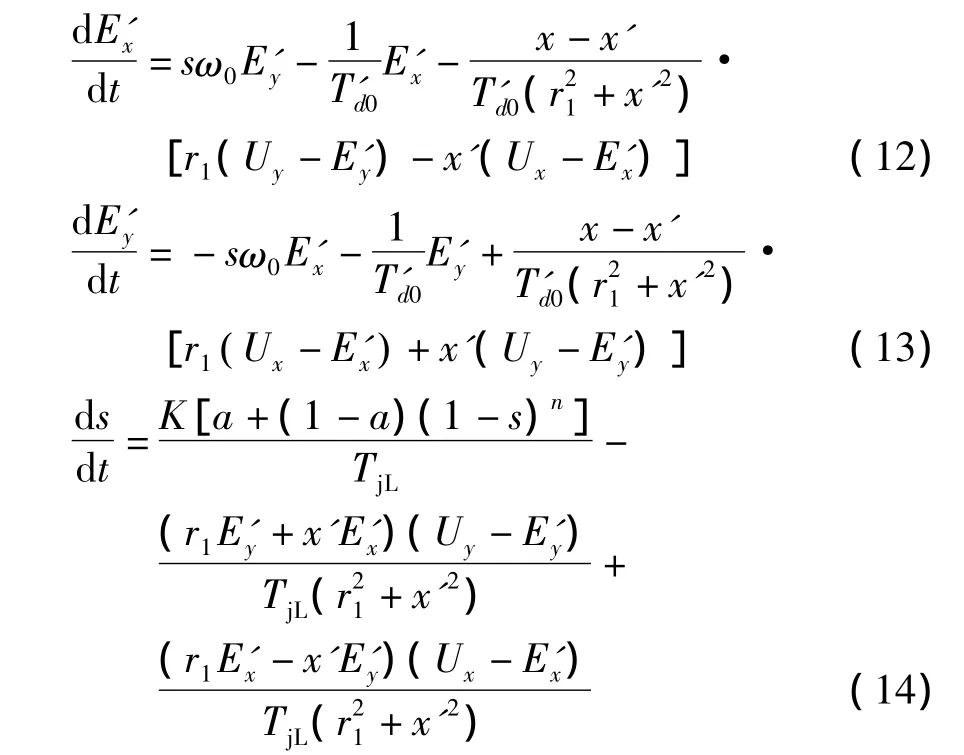
式中:E'x、E'y为电动机内电势;s为转差率;ω0为电动机开路角速度;Ux、Uy为电动机x、y轴电压;T'd0和TjL为电动机转子开路时间常数和惯性时间常数;r1为电动机定子电阻;x、x'为感应电动机同步电抗和暂态电抗;K为电动机机械功率的负载率;a为恒力矩部分;1-a为与s有关的力矩部分.
式(2)为描述网络各个节点电压电流关系的代数方程,网络节点导纳阵方程为Y˙U=˙I,则第i号节点相应的两个实数线性代数方程为

式中:(Uxi,Uyi)为 i号节点电压,Gij+jBij=Yij,Yij为Y阵中i行j列元素,(Ixi,Iyi)为i号节点注入网络的电流.
2 暂态电压稳定紧急控制
2.1 常规二级电压控制模型
二级电压控制主要目的是保证中枢母线电压等于设定值,一般通过在控制中心求解以中枢节点电压偏差最小为目标的二次规划模型实现.正常模式下二级电压控制的时间常数为几十秒到分钟级,文中取50 s,即以50 s为周期控制中心采集所有中枢母线和关键母线电压值,以及参与二级电压控制的控制机组的母线电压和有功/无功出力,求解以中枢母线电压偏差最小为目标的二次规划模型,得到发电机无功出力的调节量[14],然后通过改变发电机的自动电压调节器(AVR)的机端电压设定值(Uref)来调节发电机的无功出力,二级电压控制数学模型如下[15]:

式中:VH、Qg为发电厂高压侧母线和机组无功出力向量为发电机组无功出力的上、下限;Vp为中枢母线电压,为中枢母线电压参考值为中枢母线电压的上、下限;Cpg,Cvg为相应的控制灵敏度;Δ¯VH为发电厂高压侧母线电压控制步长,为发电厂高压侧母线电压上、下限.
采用起作用集法求解此二次规划问题,就可以得到各发电机的无功调节量ΔQg.然后根据式(17)计算得到发电机高压侧母线电压调节量ΔVH.

2.2 紧急二级电压控制模型
上述常规二级电压控制模式由于时间间隔较长,在系统发生大的扰动后的暂态过程中发挥不了作用(时间上来不及动作),因此文中提出了应对这种突发大扰动情况下的暂态电压稳定问题的紧急二级电压控制模式,由此得到三级电压控制结构如图2所示.

图2 考虑紧急二级电压控制的三级电压控制结构图Fig.2 Tertiary voltage control system structure including emergency secondary voltage control
当控制中心检测到系统发生大的扰动后,二级电压控制立即切换到紧急控制模式,紧急控制模式的控制模型不变,而控制的时间常数由正常模式下的几十秒变为5 s,应该注意的是,紧急二级电压控制的时间常数不宜设计过小,因为一级电压控制的时间常数为几秒,二级电压紧急控制的时间常数过小就会导致故障后过于频繁地调节AVR的Uref值而使电压出现过调或振荡,时间常数过大又会使AVR的调节不够及时而达不到控制故障后负荷母线暂态电压稳定的效果.经过在新英格兰39节点系统上多次的测试比较之后取5s,即当监测到系统发生大的扰动后紧急二级电压控制每5s动作一次,计算和通讯延迟时间为0.5s.
另外,在系统发生扰动后,中枢节点不一定会发生电压失稳,这样以中枢节点电压为目标的紧急二级电压控制就不能很好地保证区域内所有负荷节点的电压在暂态过程中不失稳,在下节的算例中也证明了这一点.而在系统发生故障后各个二级电压控制区域内都有一个电压跌落最严重的节点(即故障后与稳态时节点电压相比偏差最大的节点),把系统发生故障后电压跌落最严重的节点电压也引入到紧急二级电压控制的目标函数中,只要改善了该节点的电压,就可以提高全网暂态电压稳定性.
由此建立紧急二级电压控制数学模型如下:

式中:γ1、γ2为权重系数,文中均取0.5;Vc为电压跌落最严重的节点电压;为故障前电压跌落最严重的节点电压;Ccg为相应的控制灵敏度分别为电压跌落最严重的节点电压上、下限.
2.3 电压无功控制灵敏度计算
二级电压控制模型中的灵敏度是建立在潮流方程基础上的,根据PQ分解法的Q-V迭代方程:

式中:ΔQ为节点无功变化量;ΔU为节点电压变化量;B″为电导.上式中应该包括PV节点,由于发电厂PV节点具有可保持电压恒定的控制特性,进行B″求逆计算控制灵敏度时,计及PV节点物理意义,在PV节点对应 B″对角元上置极大值[16].另外,在计算被控节点对单个控制节点的无功注入的控制灵敏度时,采用逐次计算方法,即求解某发电机的控制灵敏度时,该发电机所在节点设为PQ节点,其余控制发电机节点设为PV节点.上式表明,节点无功变化与电压幅值变化强相关,对上式B″求逆可得节点之间无功电压的灵敏度关系:

式中:S=B″-1.
将式(18)的目标函数展开,去掉常数的平方项,得到标准形式的二次规划目标函数:


约束条件与式(18)的约束相同.
3 含SVC和PVC的暂态电压稳定仿真
采用时域仿真法进行暂态电压稳定分析,紧急二级电压控制模式下的时域仿真过程可以用图3来描述[17].
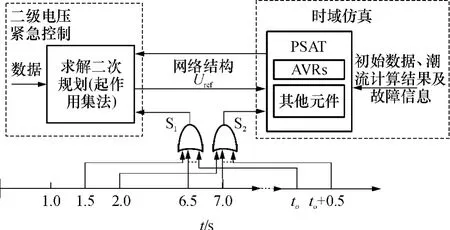
图3 含SVC和PVC的电力系统暂态电压稳定仿真过程Fig.3 Simulation process of transient voltage stability in power systems including secondary voltage control and primary voltage control
图3中暂态电压稳定仿真是在软件PSAT的仿真环境下进行的,其中发电机采用四阶实用模型,励磁系统采用三阶模型,负荷采用三阶感应电动机并联恒阻抗模型,微分方程采用隐式梯形积分法求解,代数方程采用牛顿法求解;紧急二级电压控制的二次规划模型采用起作用集法进行求解.仿真的假设条件是1.0s时系统发生故障,在1.5 s时控制中心监测到系统发生大扰动,二级电压控制立即切换到紧急控制模式,具体的仿真步骤如下.
(1)对分析计算进行初始化;
(2)计算系统初值,并形成系统稳态工况下的导纳矩阵;
(3)判断系统是否有操作或者有故障,若有操作或者故障则修改导纳矩阵及微分方程,然后根据时刻的代数方程求解时刻代数量;
(4)将系统中各元件的微分方程化为差分方程,用牛顿法联立求解系统差分方程和代数方程;
(5)判断是否进行紧急二级电压控制,若是则根据系统网络结构计算电压无功控制灵敏度,采用起作用集法求解二次规划模型得到各发电机无功调节量ΔQg,并计算出ΔVH送给各发电机端的一级电压控制器;
(6)判断是否有紧急二级电压控制的操作,若有则根据二级电压控制计算得到的ΔVH改变相应的发电机自动电压调节器的Uref值;
(7)判断是否达到仿真总时间,若达到了,则结束仿真过程,否则转到步骤(3).
4 算例分析
算例采用新英格兰39节点系统,文献[16]中采用聚类的分区方法将新英格兰39节点系统分为6个区,与文献[18]中的基于模糊聚类的分区结果一致,文中根据文献[16]的聚类过程将上述的6个区合并为3个区,分区情况如图4所示,节点28、10、20分别为各区域的中枢节点[19],系统基准功率为100MVA,系统线路和变压器参数见文献[20];负荷除31、39节点采用恒阻抗负荷外,其它节点都采用3阶感应电动机并联恒阻抗负荷,感应电动机功率占节点负荷功率的比例均为65%.考虑如下两个故障情况.

图4 新英格兰39节点系统及其分区Fig.4 New England 39 buses system and its area partition
故障1:线路5-8靠母线8处发生三相短路接地故障,经过0.20s后切除线路.
故障2:线路15-16靠母线15处发生三相短路接地故障,经过0.15s后切除线路.
当二级电压控制分别采用以下3种控制方式时,对系统进行暂态电压稳定仿真,得到上述两个故障后故障母线电压和感应电动机转差率的变化曲线如图5和图6所示.图中方式1即二级电压控制采用式(16)所示的数学模型,控制的时间常数为50s,也就是常规二级电压控制模式;方式2即二级电压控制仍然采用式(16)所示的数学模型,控制时间常数为5s;方式3即二级电压控制采用文中所提出的紧急电压控制模型,即式(18)所示的数学模型,控制时间常数为5s.
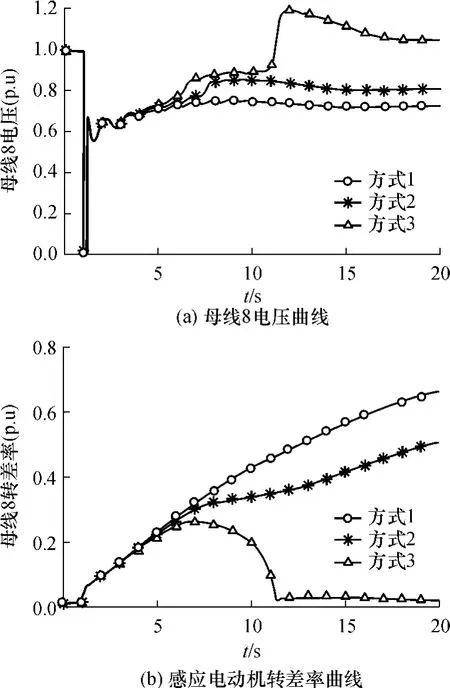
图5 故障1后在不同二级电压控制方式下母线8电压和转差率曲线Fig.5 Voltage and slip curves at Bus 8 under fault 1 correspongding to different secondary voltage control modes
由于上述故障1的短路点位置与母线8的距离远小于与其他负荷母线的距离,因而在故障1发生后母线8最先出现电压失稳,由图5(a)可以看出,在二级电压控制方式1下切除故障后母线8的电压恢复到0.72(p.u.)左右,由图5(b)看出方式1下故障切除后感应电动机转差率单调上升,判断出发生电压失稳[21];在二级电压控制方式2下切除故障后母线8的电压恢复到0.78(p.u.)左右,比方式1下的电压值有所提高,但是电动机转差率单调上升,仍然发生电压失稳;在二级电压控制方式3下切除故障9.82s后母线8的电压恢复到1.003(p.u),并且电动机转差率回落到稳定运行值,暂态电压稳定.

图6 故障2后在不同二级电压控制方式下母线15电压和转差率曲线Fig.6 Voltage and slip curves at Bus 15 under fault 2 correspongding to different secondary voltage control modes
根据上述的判断方法可知在故障2发生后母线15最先出现电压失稳,由图6(a)可以看出,在二级电压控制方式1下切除故障后母线15的电压恢复到0.7(p.u.)左右,由图6(b)可以看出方式1下故障切除后感应电动机转差率单调上升,可以判断出母线15发生电压失稳[21];在二级电压控制方式2下切除故障后7.07 s母线15的电压恢复到1.001(p.u.),并且感应电动机转差率下降到稳定运行值,暂态电压稳定;在二级电压控制方式3下切除故障后5.91s母线15的电压恢复到1.003(p.u.),感应电动机转差率下降到稳定运行值,暂态电压稳定.可见,方式3不仅能在故障后保持暂态电压稳定,并且比方式2有更快的电压恢复速度.
故障发生后在不同二级电压控制方式下各发电机的无功调节量如表1和表2所示.
二级电压控制方式1的时间常数为50 s,在故障后的10s内二级电压控制并没有动作,从表1和表2可以看出,在10 s内二级电压控制方式1下各发电机的无功调节量为0;二级电压控制方式2的时间常数为5s,得到10s内方式2下的控制时刻分别为2s和7s,从表1和表2可以得到故障1、2情况下2 s时发电机无功总增量分别为289.3 Mvar和260.04Mvar.

表1 故障1后各发电机在各种二级电压控制方式下的无功调节量ΔQGTable 1 Reactive power increments ΔQGof generators under fault 1 corresponding to different secondary voltage control modes Mvar

表2 故障2后各发电机在各种二级电压控制方式下的无功调节量ΔQGTable 2 Reactive power increments ΔQGof generators under fault 2 corresponding to different secondary voltage control modes Mvar
二级电压控制方式3的时间常数也为5 s,从表1和表2可以得到故障1、2情况下2s时发电机无功总增量分别为405.76 Mvar和320.82 Mvar,可见控制方式3比控制方式2下系统发电机无功出力的总增量明显要大,这是由于方式3的控制目标除了中枢节点电压外还引入了区域内电压偏差最大的节点电压,这样需要发电机更多的无功出力来维持系统的电压稳定.在7s时部分发电机的无功出力减少,这是由于此时这些区域的中枢节点电压已经略高于设定值.
从表1和表2还可以看出控制方式3下故障1、2发生后2s时故障所在区域发电机无功增量分别为213.00 Mvar和161.73 Mvar,故障所在区域内发电机的无功增量占到系统发电机无功总增量的50%以上,说明故障后系统的电压稳定主要通过调整故障所在区域内的发电机无功出力来控制.
通过对系统的电压仿真曲线发现在快速增大发电机无功的时候发电机端会出现短暂的电压偏高,但是这种电压偏高的幅度有限(在15%以内),并且持续时间很短(2 s以内),之后恢复到正常范围内,因此在调节发电机无功出力时伴随的这种暂时的电压偏高对系统来说是可以接受的.
5 结论
文中提出了暂态电压稳定二级电压紧急控制策略.该策略减小了故障后二级电压控制的时间常数,并把故障后电压偏差最大节点的电压也引入到协调二级电压紧急控制的目标函数中.算例分析表明,仅仅靠缩短控制时间常数的紧急二级电压控制并不能很好地保证大扰动后系统各节点的暂态电压稳定.紧急二级电压控制在系统发生大扰动后主要依靠调节故障所在区域内的发电机无功出力来控制节点电压.所提出的引入区域内电压偏差最大节点的紧急二级电压控制模式能够较好地保持系统暂态电压稳定,并且具有较快的电压恢复速度.
与低压切负荷的暂态电压稳定紧急控制手段相比,文中提出的暂态电压稳定二级电压紧急控制策略仅调节发电机无功出力,付出的代价更小,能够减少低压切负荷量,文中的两个算例均是在不切负荷的情况下使系统保持暂态电压稳定.
[1]Taylor C W.Power system voltage stability[M].New York:McGraw-Hill,1994.
[2]李立理,陆超,黄志刚.计及感应电动机的负荷节点暂态电压稳定解析评估方法[J].电力系统自动化,2009,33(7):1-5.Li Li-li,Lu Chao,Wong C K.Analytical assessment of transient voltage stability of load bus considering induction motors[J].Automation of Electric Power Systems,2009,33(7):1-5.
[3]林舜江,李欣然,刘杨华,等.考虑负荷动态模型的暂态电压稳定快速判断方法[J].中国电机工程学报,2009,29(4):4-20.Lin Shun-jiang,Li Xin-ran,Liu Yang-hua,et al.Method for transient voltage stability quick judgement considering load dynamic model[J].Proceedings of the CSEE,2009,29(4):4-20.
[4]孙华东,周孝信,李若梅.感应电动机负荷参数对电力系统暂态电压稳定性的影响[J].电网技术,2005,29(23):1-6.Sun Hua-dong,Zhou Xiao-xin,Li Ruo-mei.Influence of induction motor load parameters on power system transient voltage stability[J].Power System Technology,2005,29(23):1-6.
[5]Diaz De Leon J A Ⅱ,Taylor C W.Understanding and solving short-term voltage stability problem[C]∥Proceedings of IEEE Power Engineering Society Summer Meeting.Chicago:[s.n.],2002:742-752.
[6]薛禹胜,王正风.暂态电压安全预防控制的优化[J].电力系统自化,2006,30(9):1-4.Xue Yu-sheng,Wang Zheng-feng.Optimizaition of preventive control for transient voltage security[J].Automation of Electric Power Systems,2006,30(9):1-4.
[7]林舜江,刘明波.暂态电压安全预防控制优化的轨迹灵敏度法[J].电力系统自动化,2010,34(4):12-17.Lin Shun-jiang,Liu Ming-bo.Using trajectory sensitivity method for transient voltage security preventive control optimization[J].Automation of Electric Power Systems,2010,34(4):12-17.
[8]El-Sadek M Z.Voltage instabilities subsequent to shortcircuit recoveries[J].Electric Power Systems Research,1991,21(1):9-16.
[9]段献忠,何仰赞,陈德树.仿真计算中暂态电压稳定性的判断[J].华中理工大学学报,1995,23(4):25-28.Duan Xian-zhong,He Yang-zan,Chen De-shu.Judgment of transient voltage stability by numerical simulation[J].Journal of Huazhong University of Science and Technology,1995,23(4):25-28.
[10]徐泰山,牟宏,邱夕兆,等.山东电网暂态低电压切负荷紧急控制的量化分析[J].电力系统自动化,1999,23(21):9-11.Xu Tai-shan,Mou Hong,Qiu Xi-zhao,et al.Quantitative analysis of undervoltage load shedding system for Shan-Dong power grid [J].Automation of Electric Power Systems,1999,23(21):9-11.
[11]Milano F.PSAT [EB/OL].[2010-06-30].http://www.uclm.es/area/gsee/Web/Federico/psat.htm.
[12]倪以信,陈寿孙,张宝霖.动态电力系统的理论和分析[M].北京:清华大学出版社,2002:166-178.
[13]西安交通大学,清华大学,浙江大学,等.电子数字计算机的应用——电力系统计算[M].北京:水利电力出版社,1978.
[14]Efebvre H,Fragnier D,Bpussion J Y,et al.Secondary coordinated voltage control system[C]∥Proceedings of IEEE PES 2000 Summer Meeting.Seatle:[s.n.],2000:290-295.
[15]郭庆来,孙宏斌,张伯明,等.协调二级电压控制的研究[J].电力系统自动化,2005,29(23):19-24.Guo Qing-lai,Sun Hong-bin,Zhang Bo-ming,et al.Study on coordinated secondary voltage control[J].Automation of Electric Power Systems,2005,29(23):19-24.
[16]郭庆来,孙宏斌,张伯明,等.基于无功源控制空间聚类分析的无功电压分区[J].电力系统自动化,2005,29(10):36-40.Guo Qing-lai,Sun Hong-bin,Zhang Bo-ming,et al.Power network partitioning based on clustering analysis in mavr control space[J].Automation of Electric Power Systems,2005,29(10):36-40.
[17]Hu Bo,Cañizares Ciaudio A,Liu Ming-bo.Secondary and tertiary voltage regulation based on optimal power flows[C]∥Bulk Power System Dynamics and Control-VIII.Buzios:[s.n.],2010:1-6.
[18]杨秀媛,董征,唐宝,等.基于模糊聚类分析的无功电压控制分区[J].中国电机工程学报,2006,26(22):6-10.Yang Xiu-yuan,Dong Zheng,Tang Bao,et al.Power network partitioning based on fuzzy clustering analysis[J].Proceedings of the CSEE,2006,26(22):6-10.
[19]范磊,陈珩.二次电压控制研究(二)[J].电力系统自动化,2000,25(10):20-24.Fan Lei,Cheng Heng.Study of secondary voltage control:part two[J].Automation of Electric Power Systems,2000,25(10):20-24.
[20]周双喜,朱凌志,郭锡玖,等.电力系统电压稳定性及其控制[M].北京:中国电力出版社,2004.
[21]徐泰山,薛禹胜,韩祯祥.感应电动机暂态电压失稳的定量分析 [J].电力系统自动化,1996,20(6):12-15.Xu Tai-shan,Xue Yu-sheng,Han Zhen-xiang.Quantitative analysis for transient voltage in stability caused by induction motors[J].Automation of Electric Power Systems,1996,20(6):12-15.

