基于多参考点稳定图的斜拉桥模态参数识别*

叶锡钧 颜全胜，2 王卫锋 李健

(1.华南理工大学土木与交通学院，广东广州510640;2.华南理工大学亚热带建筑科学国家重点实验室，广东广州510640;3.伊利诺伊大学厄西纳-香槟分校环境工程学院，美国香槟61801)

对于运营中的大跨度斜拉桥，基于环境激励的模态测试是测定其动力特性的最快捷方法，而且几乎是唯一选择.自然激励技术(NExT)结合特征系统实现算法(ERA)是近年来得到广泛应用的运行模态分析方法［1-3］.但应用NExT/ERA识别模态参数时，由于系统的输入激励未知，需选择某输出点作为参考点并计算其与其他输出点的互相关函数矩阵作为输入，参考点非常重要，选择不当则不能识别某些较弱的模态.对于大型工程结构，其系统阶次未知、测试环境噪声水平较高，确定系统的阶次是模态分析的首要关键步骤.以往的方法中多数采用奇异值分解来确定系统的阶次，但得到的结果并不理想，难以剔除虚假模态.

对于此，各国的学者提出了许多不同的真实模态识别方法.Heylen等［4］提出了模态判别的模态置信度指标(MAC)和模态相位共线性指标(MPC)，以此来区分真实模态和噪声模态;Pappa等［5］以航空飞机的方向舵为试验对象，利用ERA方法识别模态参数，通过对一致模态指标(CMI)和阻尼比设置阈值筛选真实模态;李炜明等［6］通过MAC、扩展模态置信度指标(EMAC)、MPC、CMI值剔除虚假模态，识别框架模型的模态参数.

在各种方法中，稳定图方法［7-8］是一种比较理想的确定系统阶次的方法，可以从诸多模态中判别真假模态，文中将对基于ERA的稳定图方法进行改进，提出多参考点的稳定图算法，并利用该方法和增强频域分解法对崖门大桥的模态测试数据进行分析和比较.

1 增强频域分解法

频域分解法(FDD)基于谱密度矩阵的对角线化，是峰值拾取法的延伸，其原理最初由Prevosto［9］提出，Brincker等［10］对其进行了重新定义，并命名为频域分解法.FDD是通过对响应谱密度函数矩阵进行奇异值分解(SVD)，将其分解为一组单自由度系统的自功率谱，各单自由度系统自功率谱曲线峰值对应的频率就是系统的特征频率.确定特征频率后，可利用半功率带宽法确定对应的阻尼比.后来，Brincker等［11］对FDD进行了延伸，提出了增强频域分解法(EFDD)，将经奇异值分解后的单自由度自功率谱进行逆傅里叶变换，得到其对应的自相关函数，从而通过对数衰减法获得频率和阻尼比.

2 基于ERA的多参考点稳定图算法

2.1 NExT/ERA

NExT法是由James等［12］于 1993年提出，其基本思想是利用白噪声环境激励下结构两点之间响应的互相关函数和脉冲响应函数具有相似表达式的特点，将响应之间的互相关函数代替传统时域模态分析法中的自由振动响应或脉冲响应函数，进而结合其他时域模态识别方法进行模态参数识别.NExT法的计算有两种方法:一种是在时域里采用卷积算法直接计算得到;另一种是先计算出实测信号的互功率谱，再经傅里叶逆变换得到实测互相关函数［13］.文中采用后者，由于其采用了统计平均处理，即使会受到一定的谱泄漏的影响，所得到的互相关函数的信噪比也有较大幅度的提高.

ERA是多输入多输出的时域模态参数识别方法，由Juang等［14］于1984年提出，其利用实测的脉冲响应函数为基本模型构造广义Hankel矩阵，运用奇异值分解方法，确定系统的阶次和状态方程中的系统矩阵A、输入矩阵B和输出矩阵C，进而求解系统矩阵A的特征值问题，求得极点与留数，从而确定系统的模态参数.

2.2 基于输出矩阵的一致模态指标(CMI_O)

Pappa和Elliott在文献［15］中提出了一致模态指标，其计算根据EMAC和MPC，公式如下:

其中:i表示第i阶振型;j表示第j个输出点，k表示第k个输入点;EMACijk表示第i阶振型下，对应j-k(输出-输入对)的EMAC值;EMAC和EMAC分别是基于输出矩阵C和输入矩阵B的EMAC值.

Yun［16］对CMI值进行改进，提出基于输出矩阵的模态一致性指标(CMI_O)，并通过数值算例验证了在基于环境激励的模态分析过程中，CMI_O比CMI更具可靠性.

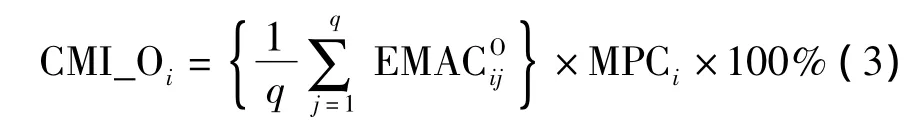
式中，q表示输出点的数量.

2.3 改进的稳定图算法

基于Pappa和James在文献［5］中应用的模态判别方法，文中提出一种基于ERA的多参考点稳定图算法，以CMI_O代替CMI作为判别准则，文中选取CMI_O阈值为75%.算法包括3个过程，如图1所示.

图1 多参考点稳定图算法的3个过程Fig.1 3 parts of the multiple reference DOFs stabilization diagram algorithm

算法步骤如下:

步骤1 选定初始参考点r，设定不同的系统阶次，运用NExT/ERA识别出不同阶次下的模态参数;每个阶次下识别出的模态参数，若能通过阈值“0＜阻尼比＜10% ＆CMI_O＞75%”，则认为是可信度较高的模态参数，进入下一步判别，共有N个模态参数;

步骤2 通过设置Δf，将步骤1中的N个模态归结为M组(每个组里各个模态相互间的频率差值小于Δf，可以认为是同一阶的频率)，不符合该要求的模态将被记录下来，当参考点为r+1时重复这一步判别;

步骤3 判断M组模态中每一组里模态的数目T，当T＞10时，认为该模态是真实模态(否则将被记录下来，当参考点为r+1时重复这一步判别);同时寻找每一组中CMI_O最大值对应的模态作为本阶段结果，得到P阶模态;

步骤4 通过步骤3可以在稳定图上清晰看到稳定轴，计算P阶模态中任意两阶之间的MAC值，小于70%的则认为都是真实模态;若大于70%，对应CMI_O值较大者则认为是真实模态;得到参考点为r时的模态参数组Set(r)，在稳定图上以红点标记;

步骤5 参考点位置为r+1，依步骤1-4得到Set(r+1).比较Set(r)和Set(r+1)同一阶模态的CMI_O，若 CMI_O(modei(r))＞CMI_O(modei(r+1))，则把Set(r+1)中的modei(r+1)用 Set(r)中的modei(r)代替(CMI_O值较大者认为更准确);若Set(r)中有Set(r+1)没有出现的模态，则加到Set(r+1)中，得到新的参数组 Set＇(r+1);

步骤6 改变参考点位置为r+2，重复步骤1-4得到Set(r+2)，再根据步骤5比较 Set＇(r+1)和Set(r+2)得到Set＇(r+2)，直到最后一个测点作为参考点，得到最终的模态参数.

算法流程图如图2所示.

图2 多参考点稳定图算法流程图Fig.2 Flowchart of the multiple reference DOFs stabilization diagram algorithm

3 崖门大桥模态测试

3.1 工程概况

崖门大桥是广东省西部沿海高速公路建设项目的重点工程之一.大桥位于广东省西部沿海高速公路斗门雷蛛至新会古斗段，为双塔单索面预应力混凝土斜拉桥，采用塔梁固结柔性墩体系.每侧边跨设置一个辅墩，跨径组合为50 m+115 m+338 m+115 m+50 m，全桥总长668 m.主梁是单箱五室预应力混凝土梁，梁高3.48m，桥面全宽26.8m.主墩为双壁柔性墩，横向宽12 m，双壁之间中心距6 m，墩高47.6 m.桥面以上塔柱高73.5 m，塔柱断面为单箱混凝土断面.全桥共有斜拉索200根，主梁标准索距6 m.

利用ANSYS软件，按照塔梁固结形式，采用Beam4和Link10单元建立大桥的空间杆系有限元模型，斜拉索的初始应变值按照设计索力计算给定，除采用Ernst公式修正斜拉索的弹性模量外，其他参数按照设计参数给定，模型如图3所示.

图3 崖门桥有限元模型Fig.3 Finite element model of the Yamen bridge

3.2 测试方案

斜拉索的布置为单索面，由于交通限制，只在主梁中间宽3m的分隔带上布置竖向和横向测点，见图4.

测试采用分组式，设置两个参考点不动.竖向布置45个测点，以跨中的测点22、23为参考点，分为11组，每组6个测点(第8组5个测点);横向测试共布置22个测点，只选取图4(b)中边跨偶数和中跨奇数测点，以测点19和21为参考点，分为7组，每组5个测点(第7组4个测点).设置采样频率都为160Hz，每组采样时间20min，第5组测点中测点22、23的加速度时程见图5.

图4 崖门桥立面及测点布置图(单位:m)Fig.4 Overview and measuring-points of the Yamen bridge(unit:m)

图5 第5组测点中测点22、23的加速度响应数据Fig.5 Acceleration responses of Channel 22#＆23#in group5

4 崖门大桥模态分析

从有限元计算结果得知，斜拉桥的前几阶固有频率都在10Hz以内，故选取较为平稳的数据段，把采样频率降到40Hz，对数据进行去除趋势项和平滑去噪处理后采用EFDD和NExT/ERA进行识别.限于篇幅，本节只列出竖向测试的第5组数据(group5)的模态参数识别过程.

4.1 EFDD识别过程

EFDD的分析结果如图6所示，由图6可见，在0～3Hz范围内可清晰分辨出8阶模态，其中第4和第8阶模态较弱.

4.2 基于ERA的多参考点稳定图算法识别过程

图6 EFDD识别结果Fig.6 Singular values by EFDD

对于NExT/ERA，选择的参考点不同，识别出的模态数目可能不一样.以竖向第5组测试数据为例，当参考点分别选择为测点1、3、5时，在0～3 Hz范围内分别能识别出5、4、6阶模态，结果如图7-9所示.

识别过程中有几个参数值得注意:(1)NExT计算互相关函数时的傅里叶变换抽样点数(NFFT)，Caicedo［17］根据不同的 NFFT，运用 NExT/ERA 识别模态参数，得到的结果差异性不大，说明该算法对NFFT不敏感，文中选择NFFT=4096，窗函数选取汉宁窗，重叠率设为50%;(2)Hankel矩阵的维数，Juang和Pappa［14］建议构造Hankel矩阵的列数约为感兴趣模态数的20倍，行数为列数的2～3倍，据此，文中构造的Hankel矩阵为600×300;(3)阻尼比阈值，受环境激励的钢筋混凝土结构，其阻尼比一般都小于5%［18］，但由于阻尼比的识别精度较低，文中放宽阻尼比阈值，取10%;(4)CMI_O阈值，Yun在文献［16］中根据数值算例的分析结果，建议CMI_O取85%，但对于大型结构的实测数据，可能由于噪声的影响或激励的不充分，致使某些模态比较弱，故文中取CMI_O=75%;(5)Δf的取值，对于文中分析实例，其各阶模态频率值(0.395，0.611，0.962，1.461，1.964，2.571 Hz，见表 1)相互间的差值都大于0.2Hz，选取Δf=0.1 Hz在步骤2中能有效地分辨出各阶模态.但对于模态密集的情况，Δf需取较小值;(6)T的取值，文中设置系统阶次为10，20，30，…，300，共 30 个阶次，识别每组数据所需的时间约为5min，取T=10，能有效排除由于噪声和计算所造成的虚假模态，若想缩短计算时间，可相应地改变系统阶次的最大值、步长和T值;(7)MAC的取值，MAC表示两组振型的相关性，当MAC=1时，表示两组模态完全相关，当MAC=0时，表示完全无关，这里取MAC=70%，能进一步确保识别出的两阶模态的低相关性.

图7 参考点为通道1时group5的稳定图Fig.7 Stabilization diagram of group5(set Channel 1#as reference DOF)

图8 参考点为通道3时group5的稳定图Fig.8 Stabilization diagram of group5(set Channel 3#as reference DOF)

图9 参考点为通道5时group5的稳定图Fig.9 Stabilization diagram of group5(set Channel 5#as reference DOF)

4.3 结果与比较

各组的频率和阻尼比识别结果如图10、11所示.观察1-11组的模态参数，在每组里面都出现的模态认为是真实模态.对于EFDD，求1-11各组模态参数的平均值为最终结果;对于多参考点稳定图，对比各组里同一阶模态的CMI_O值，最大值为最终识别结果.两种方法的最终识别结果如表1所示.

图10 各组的固有频率识别结果Fig.10 Identified natural frequencies from different group

图11 各组的阻尼比识别结果Fig.11 Identified damping ratios from different group

表1 最终模态参数识别结果Table 1 Final identified modal parameters

从图10、11和表1看出，文中算法与EFDD识别的结果基本符合，但识别结果与有限元计算结果存在一些差别.两种方法识别的频率结果较为接近，但阻尼比结果差异较大.文中算法识别的阻尼比呈从低阶到高阶逐渐递减的趋势;EFDD识别的阻尼比结果比文中算法的识别结果大，且没有变化规律，这是由于EFDD在识别阻尼比时需进行反傅里叶变换，在时域内通过指数衰减法来实现，受截断误差的影响，精度不高.

按最大位移值归一化方法，将振型向量中各元素除以最大值，得到归一化振型.限于篇幅，文中只列出竖向和横向的前3阶归一化振型，如图12-17所示.

图12 第1阶竖向振型Fig.12 1st vertical bending mode

图13 第2阶竖向振型Fig.13 2nd vertical bending mode

图14 第3阶竖向振型Fig.14 3rd vertical bending mode

图15 第1阶横向振型Fig.15 1st transverse bending mode

图16 第2阶横向振型Fig.16 2nd transverse bending mode

图17 第3阶横向振型Fig.17 3rd transverse bending mode

5 结语

对于基于环境激励的运行模态分析，使用CMI_O代替CMI作为阈值，通过设置不同的参考点计算互相关函数作为输入，基于ERA的多参考点稳定图能有效地分辩虚假模态和避免真实模态的遗漏，准确地识别出低阶模态参数，能为有限元模型的修正提供很好的依据.

文中提出的算法中的几个关键参数(阻尼比阈值、CMI_O、Δf、系统阶次的设定和T的取值、分辨两组模态相关性高低的MAC值)的取值带有较大的主观性.对于这些参数，虽然文中就工程实例崖门大桥展开了一定的讨论.但针对不同的工程实例，除要求工作者有一定的模态分析经验外，还需先对该实例的动力特性有一定的先知了解，并且识别结果的好坏在一定程度上还取决于模态试验的效果、噪声水平和激励是否充分.因此，本算法还需更进一步改进，做到能更自动地选取关键参数进而识别模态参数.

［1］He X，Moaveni B，Conte J P，et al.Comparative study of system identification techniques applied to New Carquinez Bridge［C］∥Proceedings of the 3rd International Conference on Bridge Maintenance，Safety and Management.Porto:Taylor ＆ Francis，2006:259-260.

［2］Nayeri R D，Tasbihgoo F，Wahbeh M，et al.Study of timedomain techniques for modal parameter identification of a long suspension bridge with dense sensor arrays［J］.Journal of engineering mechanics，2009，135(7):669-683.

［3］Chiang D Y，Lin C S.Identification of modal parameters from ambient vibration data using eigensystem realization algorithm with correlation technique［J］.Journal of Mechanical Science and Technology，2010，24(12):2377-2382.

［4］Heylen W，Lammens S，Sas P.Modal analysis theory and testing［M］.Leuven:Department of Mechanical Engineering，Katholieke University Leuven，1995.

［5］Pappa R S，James G H，Zimmerman D C.Autonomous modal identification of the space shuttle tail rudder［J］.Journal of Spacecraft and Rockets，1998，35(2):163-169.

［6］李炜明，朱宏平，吴贤国，等.未知激励下框架结构系统辨识的特征系统实现算法［J］.振动与冲击2010，29(8):228-231.Li Wei-ming，Zhu Hong-ping，Wu Xian-guo，et al.System identification based on experimental responses of a frame structure with unknown inputs ［J］.Journal of Vibration and Shock，2010，29(8):228-231.

［7］Peeters B，De Roeck G.Reference based stochastic subspace identification for output-only modal analysis ［J］.Mechanical Systems and Signal Processing，1999，13(6):855-878.

［8］Lanslots J，Scionti M.Automatic assessment of stabilization diagrams［R］.Leuven:LMS International，TST Research ＆ Technology Development，2002.

［9］Prevosto M.Algorithmes d＇Identification des caractéristiques vibratoires de structures mecaniques complexes［D］.Rennes:INRIA de Rennes，Université de Rennes 1，1982.

［10］Brincker R，Zhang L，Andersen P.Modal identification from ambient responses using frequency domain decomposition［C］∥Proceedings of 18th International Modal Analysis Conference.San Antonio:Society for Experimental Mechanics，2000:625-630.

［11］Brincker R，Ventura C，Andersen P.Damping estimation by frequency domain decomposition［C］∥Proceedings of19th InternationalModalAnalysis Conference.Kissimmee:Society for Experimental Mechanics，2001:698-703.

［12］James G H，Carne T G，Lauffer J P.The Natural Excitation Technique(NExT)for modal parameter extraction from operating wind turbines［R］.Albuquerque:Sandia National Laboratory Report，SAND92-1666.UC-261，1993.

［13］王济 胡晓.MATLAB在振动信号处理中的应用［M］.北京:中国水利水电出版社，2006.

［14］Juang J N，Pappa R S.An eigensystem realization algorithm for modal parameter identification and model reduction ［J］.Journal of Guidance，Control and Dynamics，1985，8(5):620-627.

［15］Pappa R S，Elliott K B.Consistent-mode indicator for the eigensystem realization algorithm［J］.Journal of Guidance Control and Dynamics ，1993，16(5):852-858.

［16］Yun G J.Modal identification and damage detection for structural health monitoring under ambient vibration environment［C］∥Structures Congress 2009.Austin:American Society of Civil Engineers，2009:1181-1190.

［17］Caicedo J M，Dyke S J，Johnson E A.Natural excitation technique and eigensystem realization algorithm for phase I of the IASC-ASCE benchmark problem:Simulated data［J］.Journal of Engineering Mechanics，2004，130(1):49-60.

［18］Filipe M，Elsa C，Álvaro C.Challenges in the application of stochastic modal identification methods to a cablestayed bridge［J］.Journal of Bridge Engineering，2007，12(6):46-754.