精确考虑单质点体系动力二阶效应的反应谱法*

王志军 韩风霞 黄宗明

(重庆大学土木工程学院∥山地城镇建设与新技术教育部重点实验室，重庆400045)

竖向重力荷载在已变形的结构中会产生对应于柱自身挠曲的P-δ效应和对应于柱端侧移的P-Δ效应两类二阶效应.从最早的经典稳定理论的单一“增大系数－计算长度”方法，到分别准确考虑P-δ效应和P-Δ效应所引起的附加变形和附加内力特点的各种简化方法(如“层增大系数法”和“全楼增大系数法”)，研究者已对静力二阶效应进行了大量的研究［1-6］.但对竖向荷载在地震作用下产生的侧移引起的二阶效应(即动力二阶效应)则研究较少，大都仅限于单质点体系的P-Δ效应［7-9］，对于同时考虑P-Δ和P-δ效应(即精确考虑二阶效应)的研究鲜见报道，也没有形成完整和方便的考虑动力二阶效应的简化方法.

现行各国规范中有关考虑二阶效应的规定，绝大部分是考虑静力二阶效应的方法.GB50011—2010《建筑抗震设计规范》根据影响静力二阶效应(主要是P-Δ效应)的稳定系数，给出了需考虑重力二阶效应的条件.我国即将颁布的《混凝土结构设计规范》［10］虽全面修订了考虑二阶效应的方法，采用了全新体系，但这套体系也主要是针对静力二阶效应的，特别是规范中考虑P-Δ效应的“层增大系数法”和“全楼增大系数法”均是考虑静力二阶效应的方法.JGJ3—2002《高层建筑混凝土结构技术规程》中考虑P-Δ效应的方法和新修订的《混凝土结构设计规范》相同.

静力二阶效应主要和稳定系数相关，稳定系数越大，静力二阶效应越大.在地震作用下，二阶效应会增大结构的侧移，也就是会使结构的侧向刚度减小，引起结构的周期改变，从而影响结构的动力响应.也就是说动力二阶效应，除和稳定系数相关外，还和结构的动力特性相关.以静力的方法来考虑动力二阶效应不能反映出结构的动力特性和地震波的频谱特性对动力二阶效应的影响.

弹性反应谱理论仍是现阶段抗震设计的最基本理论，无论是底部剪力法还是振型分解反应谱法都要用到单自由度体系的加速度反应谱.因此，研究如何利用弹性反应谱来考虑单质点体系动力二阶效应的简化方法，具有重要的理论意义和实用价值.

1 精确考虑静力二阶效应的刚度折减系数

单自由度杆体系模型如图1所示.

图1 模型示意图Fig.1 Model schemes

当只考虑P-Δ效应时，杆上距杆底部x高度处的截面弯矩M为

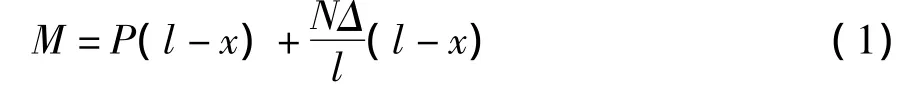
式中:P为作用在杆顶的水平力;N为作用在杆顶的竖向力;Δ为杆顶侧向位移;l为杆的长度.

弯矩M和曲率有如下关系:

式中，y为杆上距杆底部x高度处的侧向位移.

将式(1)代入式(2)并积分得到

其中:EI为截面抗弯刚度;将边界条件x=l，y=Δ代入式(3)，且令柱刚度，稳定系数，得:

上式中:

α1是只考虑静力P-Δ效应的位移增大系数，与规范中的“层增大系数”相一致.式(4)可改写为

故α1也可视为考虑P-Δ效应的侧移刚度折减系数.

当同时考虑P-Δ效应和P-δ效应时，需考虑柱自身挠曲所产生的附加弯矩，此时杆上距杆底部x高度处由竖向力产生的截面附加弯矩为N(Δ－y)，同理有:

解方程(7)得:

令

α2即为精确考虑静力二阶效应的位移增大系数或者视为侧移刚度折减系数.

2 精确考虑动力二阶效应的反应谱法

2.1 通用反应谱法

式(4)和(9)说明二阶效应的影响可视为结构刚度折减，从而使杆件侧移增大.对于动力问题，如果结构的质量不变，刚度发生改变必然导致结构周期变化.

为了研究二阶效应对结构动力响应的影响，首先建立水平地震作用下考虑了二阶效应的结构动力学方程.设杆上距杆底部x高度处的截面侧向位移为u，地面运动加速度为¨ug，图1所示的单自由度杆模型上所受的惯性力为m(¨u+¨ug)，阻尼力为c˙u，而考虑了二阶效应的恢复力则为，故单质点体系的运动方程为

其中:m为杆件集中质量;c为杆件的阻尼;αi为侧移刚度折减系数，i=1，2分别表示只考虑P-Δ效应和精确考虑静力二阶效应.

从上式可以看出，在水平地震作用下，考虑二阶效应后的结构响应，可以等效为一刚度折减为K/αi的单自由度体系的一阶响应.

假定杆的一阶周期为T0，则考虑二阶效应后的结构周期为分别表示对应 T0和Ti的位移反应谱幅值，考虑二阶效应后的位移增大系数为

根据弹性加速度反应谱Sa和位移反应谱Sd之间的近似关系，可以得到利用单条地震波加速度反应谱计算的位移增大系数为

故

式中:i=1，2，分别表示只考虑P-Δ效应和精确考虑静力二阶效应下对应的值;Sa0、Sai分别表示对应T0和Ti的加速度反应谱幅值.

从式(14)可以看出，在弹性范围内，动力二阶效应的影响取决于杆件的稳定系数和一阶、二阶周期对应的加速度反应谱值的比值.也就是说，除稳定系数外，动力二阶效应还与结构自振周期和地震波的频谱特性相关.如果已知单条地震波的加速度反应谱和结构的一阶周期，就可以根据考虑二阶效应的刚度折减系数计算出动力二阶效应影响系数.

2.2 规范设计反应谱法

为了简化计算，可根据GB50011—2010《建筑抗震设计规范》采用的设计反应谱计算动力二阶效应的位移增大系数.下面根据周期T0和Ti的大小来说明动力二阶效应影响系数的计算方法.

当T0和Ti位于规范反应谱的平台段时，Sa0=Sai，故动力二阶效应的增大系数和静力二阶效应相等.其它情况下动力二阶效应的增大系数用下式计算.

当 0≤T0≤0.1s时，

当Tg＜T0＜5Tg时，

当 5Tg≤T0≤6s时，

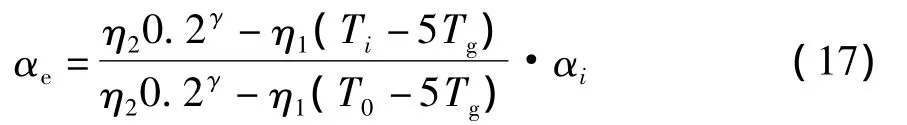
式中:Tg为特征周期;γ为衰减指数;η1为直线下降段的下降斜率调整系数;η2为阻尼调整系数;各参数均按《建筑抗震设计规范》进行取值.

从式(15)－(17)可以看出，结构自振周期T0≤0.1s时，动力二阶效应要大于静力二阶效应;当T0＞Tg后，按规范设计反应谱计算的动力二阶效应增大系数要小于静力二阶效应.以Tg＜T0＜5Tg下降段为例来进行分析，按GB50011—2010《建筑抗震设计规范》取γ=0.9，顶点侧移的静力和动力增大系数αi和αe的差别如图2所示.

图2 动力和静力二阶效应比较Fig.2 Comparision between static and dynamic second-order effects

从图2可以看出，只考虑P-Δ效应和同时考虑P-Δ和P-δ效应两种情况下，动力二阶效应的影响均小于静力二阶效应，随着稳定系数的增大，静力二阶效应的影响增加幅度较大，而动力二阶效应的影响增加幅度较小，两者的差别更加明显.

Tg＜T0＜5Tg时，P-δ效应在静力和动力二阶效应中所占的比例如图3所示.

图3 P-δ效应比例Fig.3 Proportion of P-δ effect

从图3可以看出，P-δ效应产生的影响，在静力分析中比较显著，所占的比例最大可达9.5%左右，而在动力分析中占的比例相对来说要小一些，最大在5%左右.同时由图3可见，精确考虑二阶效应时，在稳定系数为0.4左右时，P-δ效应在静力和动力二阶效应中所占比例最大，当稳定系数过大时，无论是静力分析还是动力分析，P-δ效应所占比例逐步下降.

3 数值验证

3.1 精确考虑静力二阶效应的位移增大系数α2理论公式验证

文中利用OpenSees［11］程序进行数值计算，分别计算出不同稳定系数的一阶和二阶位移，然后得到二阶位移与一阶位移的比值(即增大系数)，与公式(10)计算的结果进行比较，如图4所示.计算结果表明，精确考虑静力二阶效应时，利用程序计算的柱端位移增大系数与理论推导公式计算的侧移增大系数(刚度折减系数)α2是吻合的.

图4 公式和数值计算结果比较Fig.4 Comparison between formula calculation results and numerical calculation results

3.2 位移增大系数αe理论公式验证

3.2.1 通用反应谱法

通用反应谱法基于式(11)的运动方程，也就是结构考虑二阶效应后的响应可以等效为刚度折减为K/αi的一阶响应.为了从数值计算上说明这一结论，文中利用OpenSees程序针对不同稳定系数的结构进行了精确考虑二阶效应的二阶分析和按刚度折减的一阶分析，部分结果见表1.由表1可见，无论位移还是加速度，两者的误差都很小，充分说明刚度等效方法是正确的.

为了考察通用反应谱法在推导过程中所做简化的误差大小，文中进行了大量的有限元数值分析.分析对象为稳定系数为0.15、0.20、0.25和0.30四组悬臂柱，输入的地震波为1条天然波(El-Centro波)和3条人造地震波(Acc1，Acc2，Acc3).做出这4条波的加速度反应谱，分别按悬臂杆一阶和二阶的周期查出对应的加速度反应谱幅值，根据公式(14)计算出位移增大系数αe，即表2中的理论公式计算结果.数值计算采用Opensees程序计算，同样给出悬臂杆二阶和一阶位移的比值，结果如表2所示.从表2可以看出，采用单条地震波的通用反应谱法计算的动力二阶效应影响与数值计算结果吻合较好.

表1 程序二阶分析与折减刚度一阶分析计算结果Table 1 Results between second-order analysis and stiffness reduction method

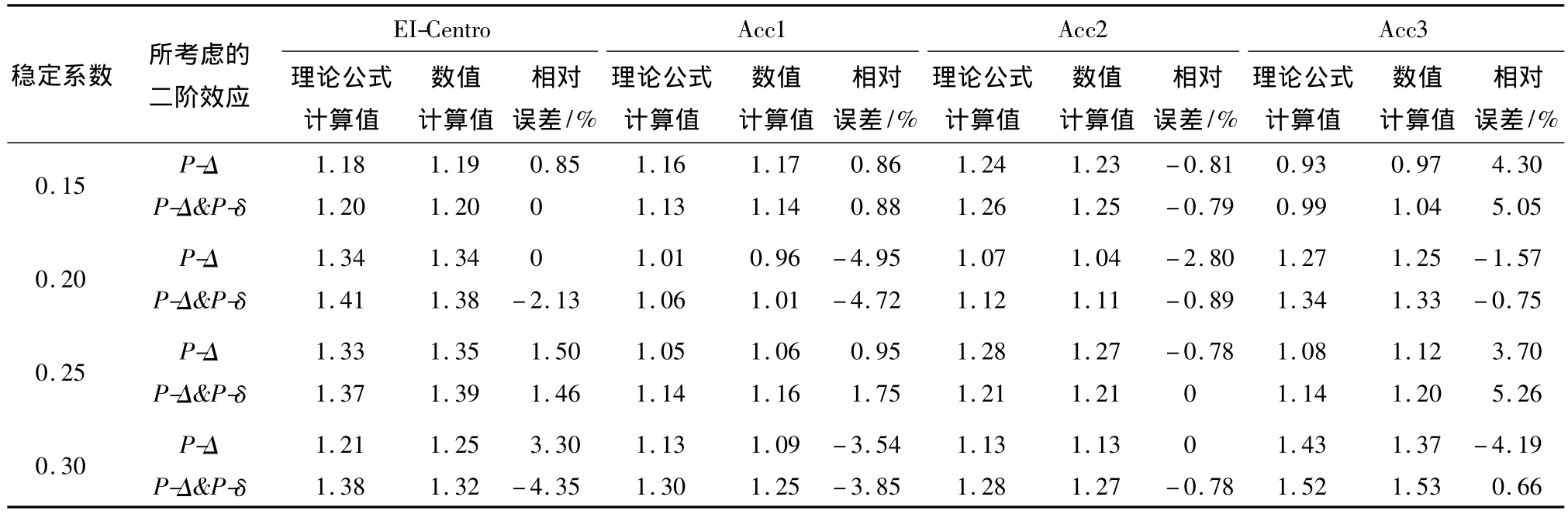
表2 通用反应谱法理论与数值计算结果Table 2 Calculation results by general seismic response spectrum method

3.2.2 规范反应谱法

假定Tg=0.35s，取结构的自振周期T0在Tg～5Tg之间，可以用公式(16)来计算规范反应谱的结果。规范反应谱法计算结果与3.2.1节的单条地震波的数值计算结果如表3所示.

从理论与数值结果比较来看，两者是有差别的，产生误差的原因在于规范反应谱是统计意义上的谱值，是多条波“平均”的结果，反应谱曲线是光滑的，而程序计算时采用的是单条地震波，其反应谱曲线并不光滑，存在小的峰值点，从而导致其结果可能小于或大于规范反应谱的计算结果.将4条波的计算结果取平均值，就与理论公式结果比较接近，误差较小.

表3 规范反应谱法与单条波数值计算结果Table 3 Results of standard response spectrum method and single seismic wave numerical calculation

4 结论

(1)从“刚度折减”的角度，研究了同时考虑P-Δ和P-δ效应对结构动力响应的影响，研究表明:在水平地震作用下，二阶效应对结构动力响应的影响，可以视为结构侧移刚度的折减;二阶效应使得结构侧移刚度减小，自振周期增大;除稳定系数外，动力二阶效应还与结构自振周期和地震波的频谱特性相关.

(2)推导了精确考虑二阶效应的结构侧移刚度折减系数;根据单条地震波的反应谱或规范设计反应谱，推导了简单方便计算动力二阶效应的位移增大系数公式.

(3)通过理论公式和程序数值分析结果对比，验证了动力二阶效应反应谱法的可行性和准确性.

［1］Lai S M A，MacGregor J G.Geometric nonlinearities in unbraced multistory frames［J］.Journal of Structural Engineering(ASCE)，1983，109(11):2528-2545.

［2］Hu Y X，Zhou G，King W S.On effective length factor of framed columns in the ACI building code［J］.ACI Structural Journal，1993，90(2):135-143.

［3］王志军，白绍良，蒲心诚，等.高强混凝土有侧移柱剪力分配和二阶效应试验研究［J］.重庆建筑大学学报，2000，22(5):102-108.Wang Zhi-jun，Bai Shao-liang，Pu Xin-cheng，et al.Experimental study on shear distribution and second-order effects of HSC sway column［J］.Journal of Chongqing Jianzhu University，2000，22(5):102-108.

［4］魏巍，朱爱萍，刘毅，等.考虑P-δ效应的钢筋混凝土框架柱设计方法［J］.建筑结构学报，2006，27(5):64-71.Wei Wei，Zhu Ai-ping，Liu Yi，et al.Design methods of reinforced concrete frame column considering P-δ effect［J］.Journal of Building Structures，2006，27(5):64-71.

［5］童岳生，童申家.有侧移钢筋混凝土框架柱纵向挠曲二阶效应的分析 ［J］.建筑结构，2005，35(9):57-61.Tong Yue-sheng，Tong Shen-jia.Analysis of flexure order effect of column in RC frame ［J］.Building Structure，2005，35(9):57-61.

［6］朱杰江，吕西林，容柏生.高层混凝土结构重力二阶效应的影响分析［J］.建筑结构学报，2003，24(6):38-43.Zhu Jie-jiang，Lü Xi-lin，Rong Bai-sheng.Influence analysis of gravity second-order effect on tall concrete structures［J］.Journal of Building Structures，2003，24(6):38-43.

［7］Bernal D.Amplification factors for inelastic dynamic P-Δ effects in earthquake analysis［J］.Earthquake Engineering and Structural Dynamics 1987，15(5):635-651.

［8］彭玉斌.P-Δ效应对抗震框架非弹性动力反应影响的初步分析［D］.重庆:重庆大学土木工程学院，2008.

［9］MacRae G A.P-Δ effects on single-degree-of-freedom structures in earthquakes［J］.Earthquake Spectra，1994;10(3):539-568.

［10］GB50010—2010.混凝土结构设计规范(报批稿)［S］.

［11］Mazzoni S，McKenna F，Scott M H，et al.OpenSees users manual［R］.Berkeley:PEER，University of California，2006.