深水复合锚泊线动力特性比较分析
乔东生 , 欧进萍
(1.大连理工大学 深海工程研究中心,辽宁 大连 116024;2.哈尔滨工业大学 土木工程学院,哈尔滨 150090)
深水复合锚泊线动力特性比较分析
乔东生1,2, 欧进萍1,2
(1.大连理工大学 深海工程研究中心,辽宁 大连 116024;2.哈尔滨工业大学 土木工程学院,哈尔滨 150090)
为了研究复合锚泊线的动力特性,文章对完全相同的两根复合锚泊线,保持其他条件不变,用聚酯纤维系缆代替钢索,使锚泊线顶端张力-静位移特性曲线基本一致,然后采用数值模拟的方法对整根复合锚泊线的动力特性进行比较分析。比较两种复合锚泊线的自振频率、复合刚度和锚泊阻尼。建立复合锚泊线的二维非线性有限元动力分析模型,基于Del Vecchio(1992)提出的经验公式,采用迭代的方法计算复合锚泊线的刚度,比较上部平台分别发生慢漂和波频运动时刚度的变化。锚泊线和海床之间的接触作用基于刚性海床假定,基于Morrison公式计算锚泊线的惯性力和拖曳力荷载,给定上部平台运动时程后在时域范围内进行复合锚泊线的动力分析,通过计算锚泊线从平台运动中吸收的能量,得到锚泊系统的阻尼,比较上部平台分别发生慢漂和波频运动时阻尼的变化。
复合锚泊线;聚酯纤维;动力特性;锚泊阻尼
1 引 言
随着海洋油气资源开发逐渐地向深海领域转移,适用于深海油气开采的新装备越来越被人们所关注。近年来由于高技术纤维材料的成功开发,用其制造的人工合成纤维逐渐地应用于深海锚泊系统中。巴西石油公司自1997年开始应用聚酯纤维系缆于实际工程中,其中FPSO-2工程水深1 420 m,是世界上第一次将合成纤维系缆用于FPSO的锚泊系统[1]。
传统的悬链式锚泊系统一般采用由三段浮容重、刚度和长度都不相同的钢链和钢索组合而成的复合锚泊线,主要通过钢链和钢索的自重为上部平台提供恢复力。锚泊线上部采用钢链连接到导缆孔,中部采用钢索,而在锚泊线与海床接触处,采用一段富余的钢链作为卧链段在海床上。随着水深的不断增大,钢索和钢链的自重变得极大,相应的造价变得很高并且很不经济。聚酯纤维系缆的自重较轻,且具有较高的断裂强度,用其代替钢链—钢索—钢链复合锚泊线中的钢索被证明具有良好的经济性能。
在钢链—钢索—钢链复合锚泊线设计中,钢索和钢链假定为线弹性材料。而聚酯纤维系缆具有典型的非线性材料特征,表现在弹性模量为非定常值,随着系缆的平均张力、动张力变化幅值和周期等变化。因而,聚酯纤维系缆的动刚度特性成为影响锚泊系统动力响应分析的重要因素。
本文对完全相同的两根复合锚泊线,保持其他条件不变,用聚酯纤维系缆代替钢索,使锚泊线顶端张力—静位移特性曲线基本一致,然后采用数值计算的方法对整根复合锚泊线的自振频率、复合刚度和锚泊阻尼等动力特性进行比较分析。
2 纤维系缆的刚度特性及求解方法
2.1 刚度特性
聚酯纤维系缆是一种粘弹性材料,应力—应变关系非线性且存在应变滞后现象。在一个循环荷载作用下的聚酯纤维系缆典型的应力—应变关系如图1所示。在该循环荷载结束后,出现了残留应变,应力与应变之间产生滞后现象,形成一个滞回环。而在多次相同循环荷载作用下,Berteaux[2]给出的应力—应变关系如图2所示。随着循环次数的增加,滞回环有重叠的趋势。可以认为,当荷载的循环次数足够大时,将出现稳定的滞回环。采用一个滞回环的中心线斜率来代表该次循环的平均弹性模量,则随着循环次数的增加,该弹性模量逐渐趋于一定值。
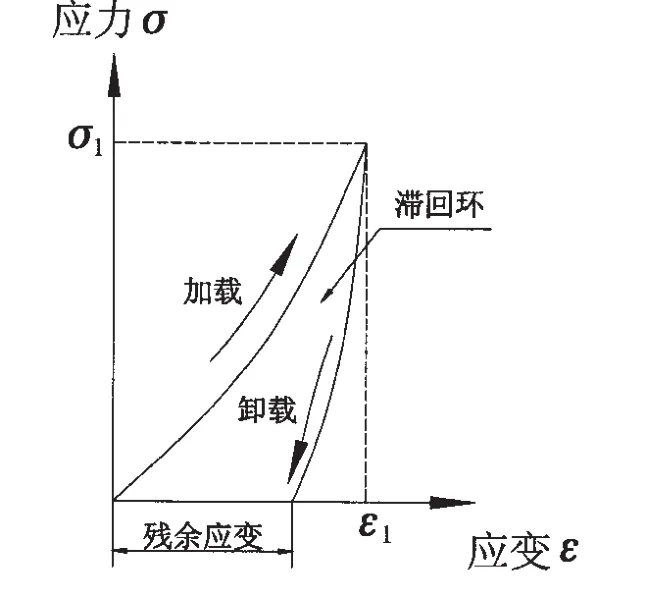
图1 单循环荷载作用纤维系缆应力—应变关系曲线Fig.1 Stress-strain curve of polyester under first loading cycle

图2 多次循环荷载作用纤维系缆应力—应变关系曲线Fig.2 Stress-strain curve of polyester under multiple loading cycle
Del Vecchio[3]给出一个常温环境条件和循环荷载作用下的纤维系缆弹性模量计算公式:

其中:E(MPa)为系缆弹性模量;ρ(kg/m3)为系缆密度;α,β,γ,δ是和纤维系缆材料特性相关的参数;Lm为平均张力占系缆最小断裂强度的百分比;La为动张力变化幅值占最小断裂强度的百分比;T(s)为动张力变化周期。
Fernandes[4]的研究表明动张力变化周期T对系缆弹性模量E的影响较弱可以忽略不计,并且通过实验进行了验证。因此,在本文计算中,系缆的弹性模量采用公式(2)计算:

其中:E(GPa)为系缆弹性模量;α′,β′,γ′是和纤维系缆材料特性相关的参数。
2.2 求解方法
从公式(2)可见,对于给定某种材料的纤维系缆,α′,β′,γ′为确定值,其弹性模量E的求解取决于平均张力Lm和动张力变化幅值La,本文采用迭代的方法求解纤维系缆的刚度,计算步骤如下:
(1)计算上部平台在稳定的风、流和二阶波浪力荷载作用下的运动响应,得到上部平台的初始平衡位置,此时导缆孔处的张力即为锚泊线顶端的初始预张力。此后上部平台在平衡位置左右做简谐振动,所以锚泊线顶端的初始预张力即为平均张力Lm;
(2)求解锚泊线的静刚度,即锚泊线在初始平衡位置时的刚度(此时La=0):预先给定锚泊线的初始迭代刚度E1,计算得到锚泊线在初始平衡位置的顶端张力,利用公式(2)计算得到锚泊线的刚度E2,重新计算得到锚泊线在初始平衡位置的顶端张力,重复迭代计算n次,直到满足 (En- En-1)≤ε 时停止迭代(ε为预先给定的容差),将计算得到的En作为锚泊线的静刚度;
(3)求解锚泊线的动刚度,即锚泊线在平衡位置左右做给定简谐振动时的刚度(此时Lm为步骤(1)求解得到的固定值):将锚泊线的静刚度作为初始迭代刚度E1,给定锚泊线顶端简谐运动时程后进行动力分析,计算得到锚泊线的动张力变化幅值La1,利用公式(2)计算得到锚泊线的刚度E2,重新进行动力分析后计算得到锚泊线的动张力变化幅值La2,重复迭代计算n次,直到满足 (En- En-1)≤ε 时停止迭代(ε为预先给定的容差),将计算得到的En作为锚泊线的动刚度。
3 阻尼计算原理
在分析锚泊线的运动响应时,一般将锚泊线假定为完全挠性构件,其运动控制方程一般采用Berteaux[2]提出的公式

其中:m,ma分别为单位长度锚泊线质量和附加质量;分别为锚泊线速度矢量和流场速度矢量;为锚泊线张力;为单位长度锚泊线净重力;,t分别为单位长度锚泊线的切向和法向拖曳力,,分别为单位长度锚泊线的切向和法向惯性力,可分别表示为:


其中:ρw为海水密度;CDt和 CDn分别为切向和法向拖曳系数;D 为锚泊线等效直径;ΔV→t和 ΔV→n分别为流体和锚泊线之间的相对切向和法向速度;CIt和CIn分别为切向和法向附加质量系数。
在一个运动周期τ内锚泊线耗散的能量E可以表示为

阻尼可以等效为线性化的阻尼系数B,所以,某一时刻的瞬时水平张力Tx可以近似表示为

假定锚泊线顶端导缆孔处的运动时程和上部平台的运动时程相同,而平台在波浪作用下的运动响应X(t)假定为正弦运动,即X=X0sin( ωt),其中X0为平台运动响应幅值。所以,一个运动周期τ内锚泊线耗散的能量E可以近似地表达为

因此,根据计算得到的一个运动周期τ内锚泊线耗散的能量E就可以得到等效线性化的阻尼系数:

其中,耗散的能量E可以通过积分一个周期内的顶端水平张力—位移曲线得到,需要利用到有限元动力计算的结果。
4 算 例
为了分析聚酯纤维系缆代替钢索对复合锚泊线动力特性的影响,计算中以图3所示的单根复合锚泊线为研究对象,比较两根复合锚泊线的自振频率、刚度和锚泊阻尼。两根复合锚泊线的材料特性如表1所示。本文计算聚酯纤维系缆的弹性模量时,材料特性参数采用α′=14.469,β′=0.211 3,γ′=0.269 7[5]。
4.1 计算模型
为保证两根复合锚泊线的动力特性具有可比性,本文通过改变复合锚泊线顶端初始预张力,使两根复合锚泊线满足顶端张力—静位移特性曲线基本一致。在计算中采用分段外推法,考虑了锚泊线的重力、张力、海流力及锚泊线的弹性伸长[6],得到两根复合锚泊线的顶端张力—静位移特性曲线如图4所示。对于复合锚泊线II,公式(2)计算中采用的是纤维系缆顶端的张力,而不是复合锚泊线顶端的张力。每次改变复合锚泊线的顶端预张力,纤维系缆的静刚度均需要重新迭代计算,相当于给定多个初始平衡位置迭代求解每个平衡位置的刚度,采用上文中给出的静刚度计算过程,具体迭代过程如表2所示。
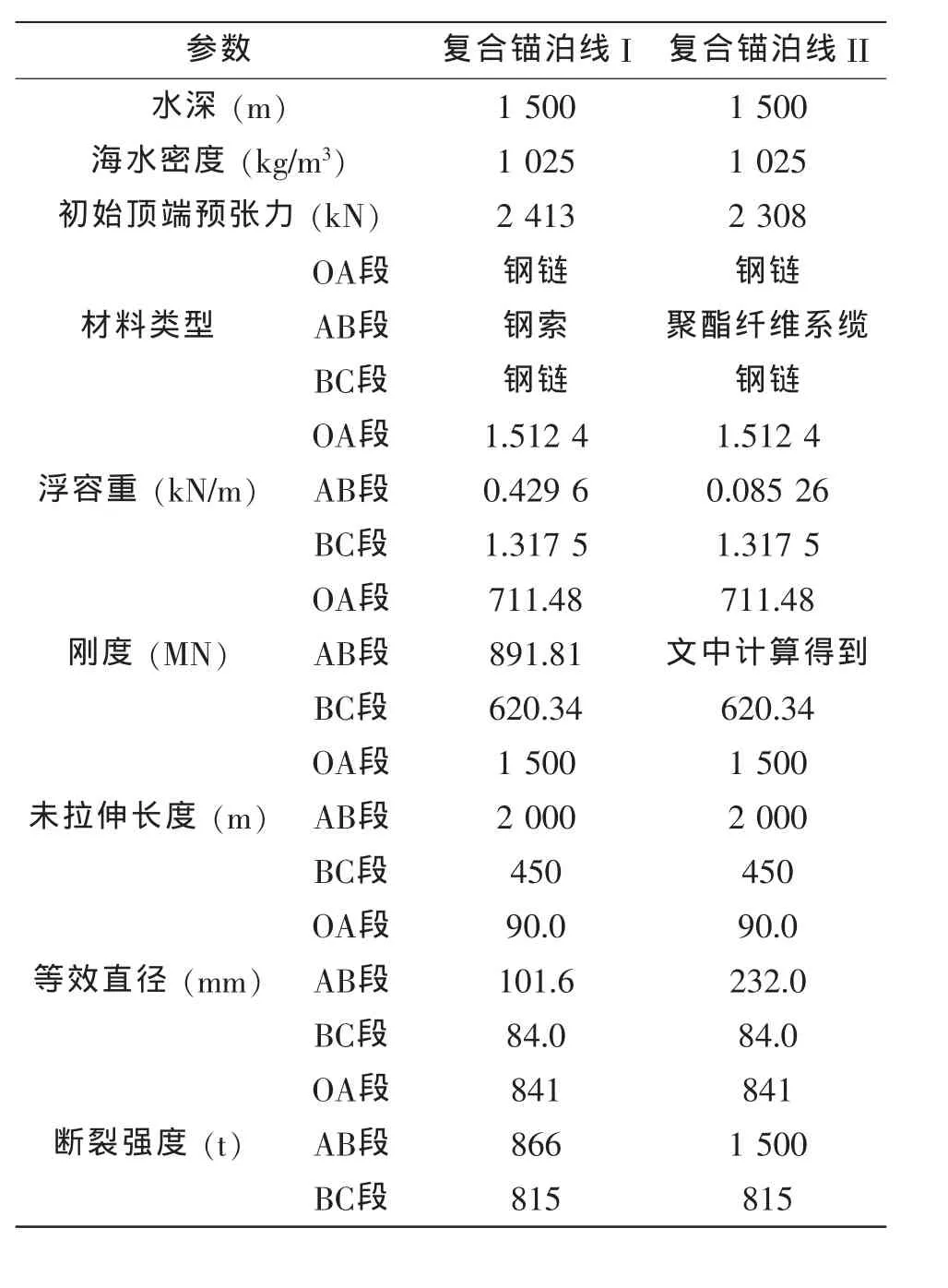
表1 锚泊线材料特性和初始找形条件Tab.1 Line physical properties and site conditions
为完成如图3所示的初始悬链线形态,采用参考文献[7]中的静力分析步骤,这样可以保证在模型中自动包括了锚泊线有关的初始应力和刚度。在动力分析时为避免突加荷载对计算结果的影响,对每种工况计算6个周期,取稳态计算结果进行分析处理。有限元模型中锚泊线采用混合梁单元进行模拟,海床采用刚性海床,忽略海床摩擦的影响。
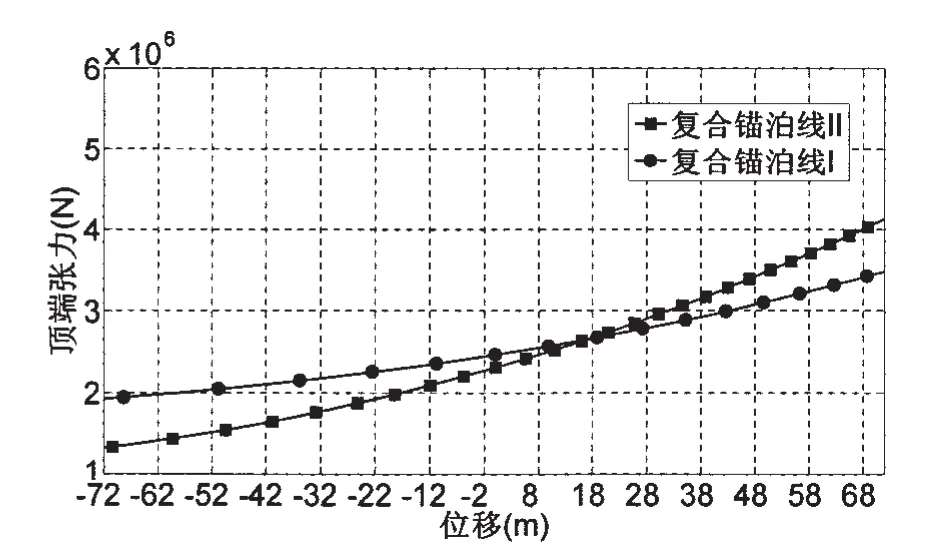
图4 顶端张力—位移曲线Fig.4 Tension-displacement characteristic curve

表2 静刚度计算过程Tab.2 Calculation process of static module
4.2 计算参数
计算中首先比较初始悬链线形态的自振频率,并考虑附加水质量对自振频率的影响。然后比较锚泊线顶端水平运动时程分别为慢漂运动和波频运动对锚泊阻尼计算结果的影响,计算的各种工况如表3所示。对应于不同工况时,复合锚泊线II的动刚度均需要通过公式(2)迭代计算,采用上文中给出的动刚度计算过程。
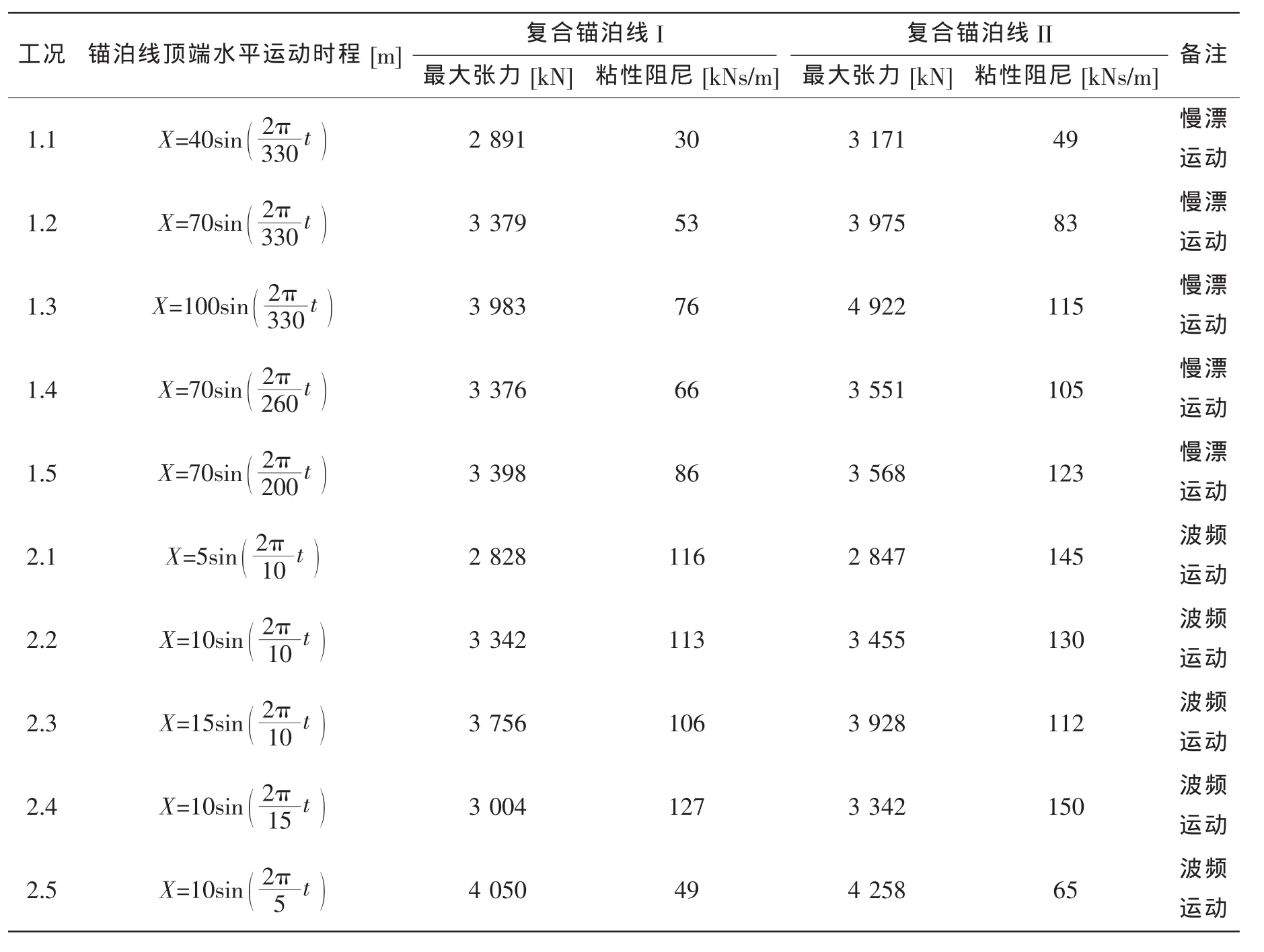
表3 计算参数Tab.3 Calculation parameters
5 结果及分析
5.1 自振频率
以图3所示的初始悬链线形态进行振型分析,分别得到复合锚泊线的前10阶频率如表4和图5所示。可见,考虑附加水质量后使锚泊线的自振频率变小,由于复合锚泊线II的自重较轻且直径较大,所以附加水质量对其自振频率的影响较大,而对复合锚泊线I的影响很小。比较同一阶频率,复合锚泊线II均比复合锚泊线I的自振频率大,表明采用聚酯纤维系缆的复合锚泊线II对波频运动激励更为敏感。
5.2 动刚度计算及比较
给定复合锚泊线II的初始顶端张力,可以在表2中得到锚泊线的初始静刚度,根据表3给定的工况,进行二维非线性有限元动力分析。利用上文中给出的动刚度计算方法,具体的迭代过程如表5所示。

图5 自振频率比较曲线Fig.5 Natural frequency curve of hybrid mooring line

表4 自振频率计算结果Tab.4 Results of natural frequency
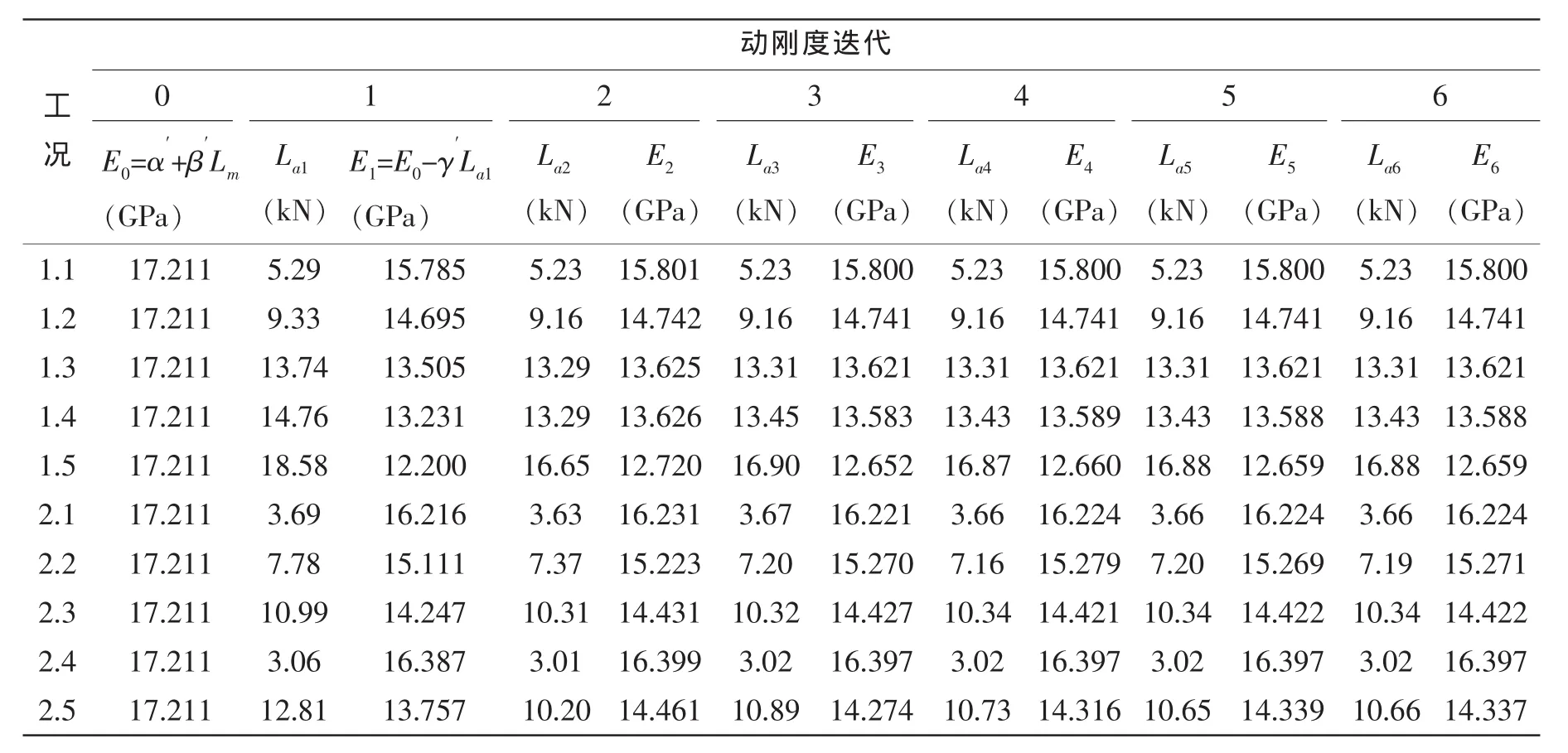
表5 动刚度计算过程Tab.5 Calculation process of dynamic module
锚泊线顶端运动时程的运动幅值对聚酯纤维锚泊线弹性模量的影响如图6所示。图6(a)为慢漂运动激励的计算结果比较,图6(b)为波频运动激励的计算结果比较。由图6可见,对于慢漂运动激励和波频运动激励,随着锚泊线顶端运动时程的运动幅值增大,聚酯纤维锚泊线的弹性模量变小,基本呈线性变化趋势。

图6 运动幅值的影响Fig.6 Influence of oscillation amplitude
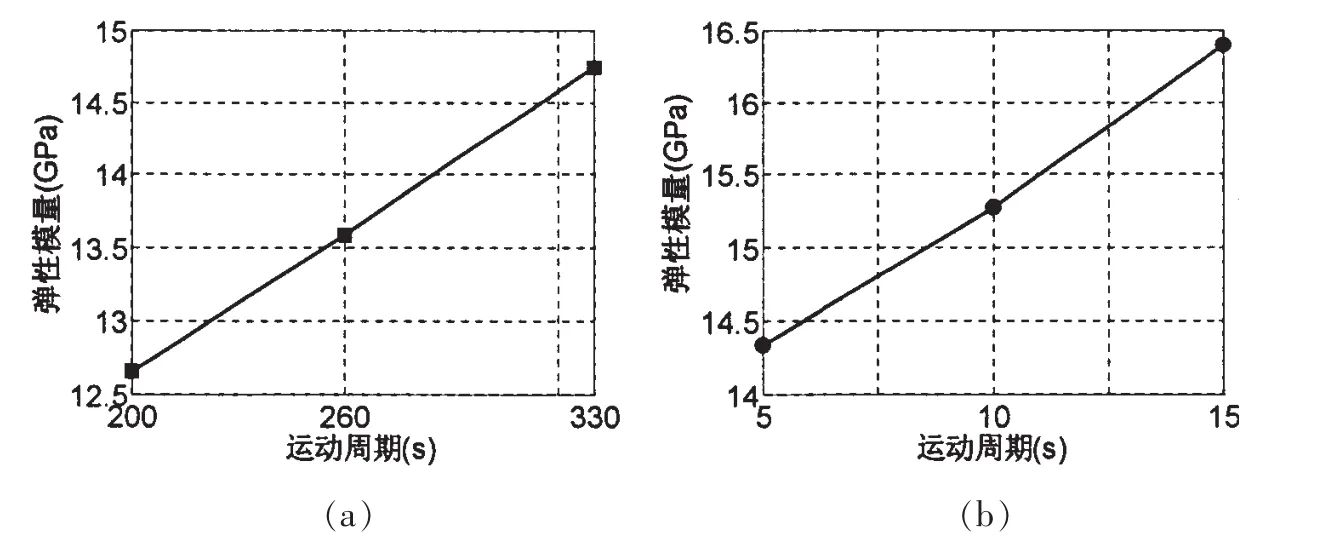
图7 运动周期的影响Fig.7 Influence of oscillation period
锚泊线顶端运动时程的运动周期对聚酯纤维锚泊线弹性模量的影响如图7所示。图7(a)为慢漂运动激励的计算结果比较,图7(b)为波频运动激励的计算结果比较。由图7可见,对于慢漂运动激励和波频运动激励,随着锚泊线顶端运动时程的运动周期增大,聚酯纤维锚泊线的弹性模量变大,也基本呈线性变化趋势。
从表5可见,满足顶端张力—静位移特性曲线基本一致的两根复合锚泊线,其中聚酯纤维锚泊线的动态弹性模量约为钢索的0.1倍,聚酯纤维系缆的动刚度约为钢索的0.66倍。
5.3 锚泊阻尼
(1)最大张力及锚泊阻尼
各种工况下锚泊线中的最大张力计算结果如图8所示,并在表3中给出了具体的数值。从图8可见:无论是慢漂运动或波频运动,顶端运动时程的运动幅值变大,锚泊线中的最大张力也变大;顶端运动时程的运动周期对锚泊线中的最大张力影响相对较小。同一工况下,复合锚泊线II中的最大张力均比复合锚泊线I中的最大张力大。
各种工况下锚泊线的粘性阻尼计算结果如图9所示,并在表3中给出了具体的数值。同一工况下,复合锚泊线II中的锚泊阻尼均比复合锚泊线I中的锚泊阻尼大,表明复合锚泊线II提供给上部浮体的阻尼力更大。

图8 最大张力Fig.8 Maximum line tension

图9 锚泊阻尼Fig.9 Mooring-induced damping
(2)运动幅值的影响
锚泊线顶端运动时程的运动幅值对锚泊阻尼的影响如图10所示。图10(a)为慢漂运动激励的计算结果比较,图10(b)为波频运动激励的计算结果比较。由图10(a)可见,对于慢漂运动激励,随着锚泊线顶端运动时程的运动幅值增大,两根复合锚泊线的锚泊阻尼均变大且变化趋势一致,但复合锚泊线II比复合锚泊线I的锚泊阻尼约增加60%。由图10(b)可见,对于波频运动激励,随着锚泊线顶端运动时程的运动幅值增大,两根复合锚泊线的锚泊阻尼均变小且变化趋势一致,但复合锚泊线II比复合锚泊线I的锚泊阻尼约增加20%。

图10 运动幅值的影响Fig.10 Influence of oscillation amplitude
(3)运动周期的影响
锚泊线顶端运动时程的运动周期对锚泊阻尼的影响如图11所示。图11(a)为慢漂运动激励的计算结果比较,图11(b)为波频运动激励的计算结果比较。由图11(a)可见,对于慢漂运动激励,随着锚泊线顶端运动时程的运动周期增大,两根复合锚泊线的锚泊阻尼均变小且变化趋势一致,但复合锚泊线II比复合锚泊线I的锚泊阻尼约增加50%。由图11(b)可见,对于波频运动激励,随着锚泊线顶端运动时程的运动周期增大,两根复合锚泊线的锚泊阻尼均变大且变化趋势一致,但复合锚泊线II比复合锚泊线I的锚泊阻尼约增加15%。
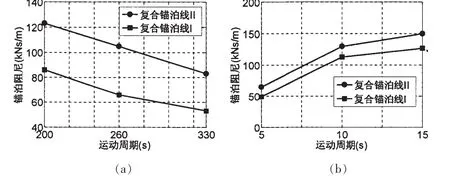
图11 运动周期的影响Fig.11 Influence of oscillation period
6 结 论
通过对完全相同的两根复合锚泊线,保持其他条件不变,用聚酯纤维系缆代替钢索,使锚泊线顶端张力—静位移特性曲线基本一致,对整根复合锚泊线的动力特性进行比较分析,可以得到以下一些结论:
(1)聚酯纤维锚泊线的弹性模量需要通过迭代方法进行求解,不同荷载工况下的静刚度和动刚度有显著差别。
(2)考虑附加水质量会使锚泊线的自振频率变小。与钢索相比,附加水质量对聚酯纤维锚泊线自振频率的影响更大。对于同一阶频率,聚酯纤维锚泊线均比钢索的自振频率大,表明采用聚酯纤维系缆的复合锚泊线对波频运动激励更为敏感。
(3)对于慢漂运动激励和波频运动激励,随着锚泊线顶端运动时程的运动幅值增大,聚酯纤维锚泊线的弹性模量变小,基本呈线性变化趋势。而随着锚泊线顶端运动时程的运动周期增大,聚酯纤维锚泊线的弹性模量变大,也基本呈线性变化趋势。
(4)满足顶端张力—静位移特性曲线基本一致的两根复合锚泊线,其中聚酯纤维锚泊线的动态弹性模量约为钢索的0.1倍,聚酯纤维系缆的动刚度约为钢索的0.66倍。
(5)对于慢漂运动激励,随着锚泊线顶端运动时程的运动幅值增大,两根复合锚泊线的锚泊阻尼均变大且变化趋势一致,但聚酯纤维锚泊线比钢索的锚泊阻尼约增加60%。对于波频运动激励,随着锚泊线顶端运动时程的运动幅值增大,两根复合锚泊线的锚泊阻尼均变小且变化趋势一致,但聚酯纤维锚泊线比钢索的锚泊阻尼约增加20%。
(6)对于慢漂运动激励,随着锚泊线顶端运动时程的运动周期增大,两根复合锚泊线的锚泊阻尼均变小且变化趋势一致,但聚酯纤维锚泊线比钢索的锚泊阻尼约增加50%。对于波频运动激励,随着锚泊线顶端运动时程的运动周期增大,两根复合锚泊线的锚泊阻尼均变大且变化趋势一致,但聚酯纤维锚泊线比钢索的锚泊阻尼约增加15%。
用聚酯纤维锚泊线代替钢索会增加锚泊线提供给上部浮体的阻尼力,但锚泊线的自振频率会变大而使其对波频运动激励更为敏感。
[1]Pedro Barusco.Mooring and anchoring systems developed in marlin field[C]//Proceedings of the Offshore Technology Conference.Houston,USA,1999.
[2]Berteaux H O.Buoy Engineering[M].New York:Wiley Interscience Publication,1976.
[3]Del Vecchio C J M.Light weight materials for deep water moorings[D].University of Reading,UK,1992.
[4]Fernandes A C,Del Vecchio C J M,Castro G A V.Mechanical properties of polyester mooring cables[J].International Journal of Offshore and Polar Engineering,1998,9(3):248-254.
[5]Kim Minsuk,Ding Yu,Zhang Jun.Dynamic simulation of polyester mooring lines[C]//Deepwater Mooring Systems:Concepts,Design,Analysis,and Materials.Houston,USA,2003:101-114.
[6]乔东生,欧进萍.深水悬链锚泊系统静力分析[J].船海工程,2009(2):120-124.
[7]Chaudhury G,Ho Cheng-Yo.Coupled dynamic analysis of platforms,risers,and mooring[C]//Proceedings of the Offshore Technology Conference.Houston,USA,2000:647-654.
Comparative analysis on dynamic characteristics of deepwater hybrid mooring line
QIAO Dong-sheng1,2,OU Jin-ping1,2
(1 Center for Deepwater Engineering,Dalian University of Technology,Dalian 116024,China;
2 School of Civil Engineering,Harbin Institute of Technology,Harbin 150090,China)
For study dynamic characteristics of the deepwater hybrid mooring line,considering the two hybrid mooring lines is completely identical while other conditions are kept unchanged,and the top end tension-static offset characteristic curve of the two mooring lines is consistent as much as possible,the polyester rope is as the substitute for the wire,then the method of numerical simulation is adopted to carry on the comparative analysis on dynamic characteristic.And the natural frequency,complex stiffness and mooring-induced damping are compared.After the establishment of two-dimensional nonlinear finite element dynamic model of the hybrid mooring line,the calculation on stiffness of the hybrid mooring line is accomplished through the iterative method based on the empirical formula proposed by Del Vecchio in 1992.When the wave drift motion and wave frequency oscillations of the floating platform are specified,the consequent variations of stiffness are compared respectively.The mooring line and seabed interaction are based on the hypothesis of rigid seabed.The fluid drag force and inertia force on the mooring line are calculated according to the Morrison formula.The dynamic analysis is executed through time-domain nonlinear finite element method accounting for the oscillations of the moored floating platform.The energy absorbed from the oscillation of the floating platform in the mooring line is worked out,and then the mooring-induced damping is achieved.Finally,the wave drift motion and wave frequency oscillations of the floating platform are specified,the consequent variations of the mooring-induced damping are compared.
hybrid mooring line;polyester;dynamic characteristic;mooring-induced damping
U675.92
A
1007-7294(2011)11-1290-10
2010-08-26 修改日期:2011-03-13
国家重点基础研究发展计划资助(2011CB013700);国家自然科学基金创新研究群体项目资助(50921001); 国家 863 计划项目(2006AA09A103,2006AA09A104)
乔东生(1983-),男,博士,研究方向为深海采油平台锚泊系统,Email:qds903@163.com;
欧进萍(1959-),男,中国工程院院士,博士生导师。

