船艉结构静动态多目标优化设计

黄海燕，林志祥，王德禹

（1.江苏科技大学 船舶与海洋工程学院，镇江 212003；2.云南农业大学 水利水电与建筑学院，昆明 650201 3.上海交通大学海洋工程国家重点实验室，上海200030）

船艉结构静动态多目标优化设计

黄海燕1，林志祥2，王德禹3

（1.江苏科技大学 船舶与海洋工程学院，镇江 212003；2.云南农业大学 水利水电与建筑学院，昆明 650201 3.上海交通大学海洋工程国家重点实验室，上海200030）

建立用于船体结构静动力学性能一体化设计优化的2种多目标优化模型：基于多目标遗传算法的多目标优化模型和基于多学科优化技术的多目标协同优化模型。模型均使用矩阵描述由板材厚度和骨材型号构成的离散设计变量集，以结构质量最小化和最大加速度最小化组成多目标函数。以某集装箱船艉部结构为例，对其进行了结构静力学、动力特性和动力响应的计算分析与优化设计。优化后的结构不仅具有更轻的质量、更低的振动水平，而且具有更高的固有频率储备，同时仍满足强度和刚度要求。

多目标优化；协同优化；动力响应；遗传算法；离散变量

1 引 言

作用在船舶结构上的荷载工况十分恶劣、复杂，这对船舶结构的静、动力学性能设计提出了更高的要求。在结构静力学性能的约束下，优化设计可以使结构的应力分布更趋合理，实现结构的轻量化。在结构动力学性能的约束下，优化设计可以在设计初期有效解决日益突出的结构振动问题。但是，单独进行结构静力学或动力学优化设计，都不能准确地反映船舶的实际工作状态。因此，船舶结构优化问题是一个多学科、多目标、多变量和多约束的优化问题。如果采用常规的优化设计方法进行设计，不仅效率很低，而且可能出现由于问题本身的复杂性而难以获得有用的优化解。

对这类问题，一般采用多目标优化方法解决。多目标优化问题中的多个目标不能同时达到最优解，而是存在一个Pareto最优集。进化算法特别适用于求解多目标优化问题[1-2]。为了尽可能提高算法的搜索效率，不断有新的算法被提出或改进[3]。多学科优化技术也是解决上述问题的有效方法之一。协同优化算法（Collaborative optimization）是多学科优化方法的一种。其基本思想是：每个子学科在设计优化时，暂时不考虑其它子学科的影响，只满足与本子学科有关的约束；子学科的优化目标是使子学科的设计优化方案与系统级优化器提供的目标方案之间的差异最小，各子学科设计优化的不一致性由系统级优化问题的学科一致性约束来协调。通过系统级优化和子学科优化之间的多次迭代，最终获得一个满足学科一致性约束的系统最优设计方案[4]。该算法已成功应用于运载火箭发射、轨道优化、超音速飞机和无人驾驶飞机等优化设计中[4-5]。但是，一致性等式约束的引入，往往会导致计算困难，同时也使得系统级优化问题一般不满足Kuhn-Tucker条件[6-7]。解决方法一般是引入约束松弛因子[6]或使用罚函数方法[7]。

另一方面，结构动力学优化设计同时涉及到结构动力特性和动力响应计算、分析和优化设计，因此求解更为困难和复杂。设计变量的离散性加剧了结构动力优化的难度。文献[8-9]对结构动力优化设计发展进行了综合评述。

基于多目标进化算法和多目标协同优化算法，论文对某集装箱船艉部结构进行了结构静、动力学特性的一体化优化设计与比较。

2 多目标优化模型

2.1 数学模型

一般情况下，船艉结构多目标优化模型的数学表达式为

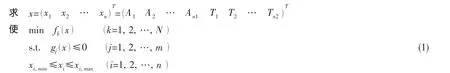
式中：xi为设计变量；n 为设计变量总数，n=n1+n2；Ai为板材厚度，共 n1个；Ti为骨材型号，共 n2个；fk（x）为目标函数，共N个；gj（x）为第j个不等式约束，共m个；xi,min和xi,max分别为第i个设计变量xi的下、上限。

（1） 目标函数

在船艉结构的静力学优化分析中，选择结构质量m最小化为目标函数；在动力学优化分析中，选择结构最大加速度amax最小化为目标函数。由这两个目标函数组成船体艉部结构多目标优化设计的目标函数。

（2） 设计变量

在船舶结构优化设计中，由于船舶的主尺度参数是确定的，所以只能选择构件尺寸作为设计变量。通常选择板材厚度和骨材尺寸为设计变量。按设计变量类型的分类，它们属于离散变量。常用的处理方法是首先获得问题的连续变量最优解，然后根据实际情况将它们圆整到合适的离散值上。这种圆整方法无规律可循，圆整后的解很有可能是不可行解，可能导致优化结果失去实际意义和应用价值。另外，当选取骨材尺寸作为独立的设计变量时，型材的尺寸参数H、W、t1、t2（如图1所示）之间的协调变化很难得到保证。因为所有的型钢

尺寸必须符合既定规格的要求，否则将会导致船厂买不到相应型号的型钢，或必须向工厂专门定制。因此，本文选取板材厚度和骨材型号为设计变量，并建立用矩阵描述的离散集。

由板材厚度构成的离散集的矩阵描述为

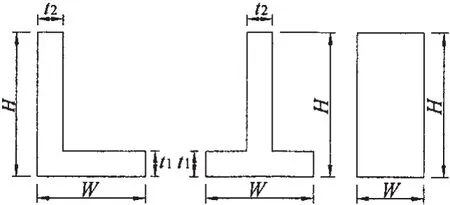
图1 骨材设计变量Fig.1 Design variables of beam

式中：Ai为第i个设计变量；Aij为第i个设计变量的第j个取值；k1为离散变量可取值的个数；为程序编写方便，规定离散值的取值顺序为Aij-1＜Aij＜Aij+1（i=1,2,…,n1;j=1,2,…,k1）。 当个数不同时，使用该设计变量的最后一个值补足。该设计变量的取值方法为：程序首先找到第i个设计变量，然后再根据优化准则在k1个取值中进行选择。

船舶结构中使用的型材截面通常有L型、T型和矩形截面等。它们均可使用四个尺寸参数描述其截面尺寸：H、W、t1、t2，如图1所示。对矩形截面骨材，t1=t2=0。由型材型号构成的离散集的矩阵描述为

式中：Ti为第 i个设计变量；（H 、 W、t1、t2）ij为第i个设计变量的第j个取值，这4个参数在程序中由一个4维数组构成；k2为离散变量可取值的个数；为程序编写方便，规定离散值的取值顺序由H的取值决定，即 Hij-1＜Hij＜Hij+1（i=1,2,…,n2;j=1,2,…,k2）。当个数不同时，使用该型材的最后一个型号补足。该设计变量的取值方法为：程序首先找到第i个设计变量，然后再根据优化准则在k2个取值中进行选择，每次选择一个型号，即一个由 4个参数（H、W、t1、t2）构成的数组。

根据约束条件和各船级社规范，确定每一个设计变量的取值集合，构成一个数据库，在每次优化时，供优化程序调用。

（3） 约束条件

约束条件主要有几何约束、强度约束、频率禁区约束和动力响应约束等。几何约束条件的一般表达式为式中：

xi,min为约束下限，一般为静力条件下限或结构合理性下限；xi,max为约束上限，一般为工艺要求上限；ns为几何约束条件个数。

强度约束条件的一般表达式为

式中：σmax和 τmax为结构最大应力；]和为许用应力。

频率禁区约束条件的一般表达式为

式中：fi为第i阶频率；fi,min、fi,max分别为频率禁区的下限和上限；nf为频率约束条件个数。

当结构具有最小加速度时，速度也必须满足相应的约束条件

式中：vmax为结构中最大速度；[]v为许用速度。

此外，还有按振动衡准要求设定的最大位移约束；考虑腐蚀和稳定性等要求设定的最小板厚约束；考虑结构合理性要求设定的最大板厚约束。

（4） 优化算法

多目标进化算法不需要事先充分了解各目标的详细信息，而利用其强大的全局搜索能力，找出可能的优化解，供决策者参考。基于精英策略的非支配排序遗传算法NSGA-II采用了快速非优超排序和排挤机制，使计算复杂性从O（mN3）降至O（mN2）；同时提高了计算效率和算法的鲁棒性。因此，在艉部结构多目标优化设计中，选用NSGA-II算法为优化算法。

2.2 优化设计流程

根据船体结构设计优化特点，基于NSGA-II算法的多目标优化设计流程如图2所示。

3 多目标协同优化模型

使用多学科优化技术对船体结构进行优化设计时，其目标函数、设计变量和约束条件的设置与上节中的多目标优化模型中的参数设置保持一致。有本质区别的是优化算法结构和优化策略。

3.1 优化算法结构

在多目标优化过程中，不同的目标可能涉及到不同的学科，其计算理论及函数值的数量级、量纲等均存在差异。图3所示的多目标协同优化MOCO（Multi-objective collaborative optimization）[10]算法结构完全可以解决这个问题。在该算法中，系统级优化不仅独立地直接调用学科级分析工具，用于计算该学科的目标函数值；同时也调用学科级优化，以获取子学科级优化所获得的目标函数和设计变量的最优解。（1）系统级优化

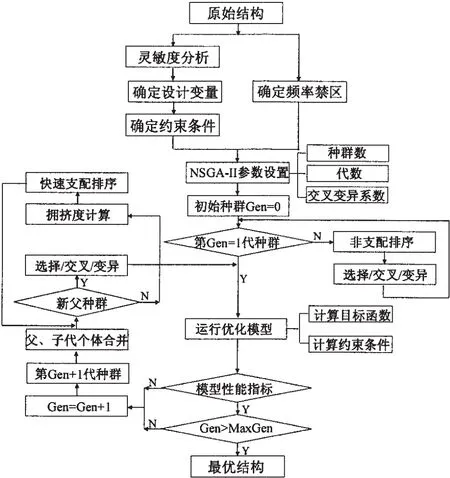
图2 基于NSGA-II算法的多目标优化设计流程Fig.2 Multi-objective optimization design flow based on NSGA-II

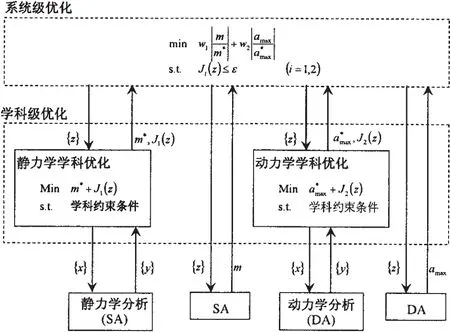
图3 多目标协同优化算法结构Fig.3 Multi-objective collaborative optimization framework

系统级优化是获得满足一致性约束条件的全局最优解。为了消除数量级和量纲的影响，在系统级优化模型中，选用各子学科的目标函数相对值为系统级目标函数。同时，为了避免无解或收敛困难的情况出现，采用引入约束松弛因子ε的方法来改造一致性约束条件。则系统级优化模型为

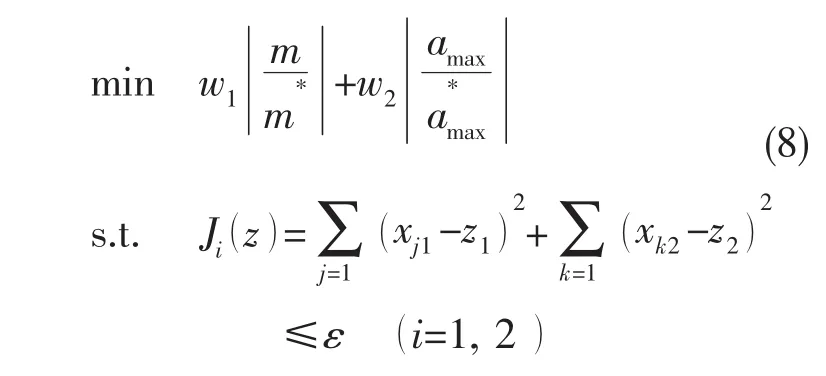
式中：m，amax分别为系统级优化模型通过静力学、动力学学科独立分析得到的目标值；m，分别为静力学、动力学优化模型得到的最优目标值；z={z1, z2}为系统级设计变量向量，z1为共享设计变量，z2为耦合设计变量；Ji（z）≤ε为子学科之间的一致性约束条件，以保证学科之间状态变量的一致性；xj1为全局设计变量，xk2为状态设计变量。

（2）学科级优化

静力学学科的优化模型为

动力学学科的优化模型为

3.2 优化策略

优化算法是一种求解策略，它通过搜索设计空间来求解优化问题。优化算法种类很多，需要根据实际问题有目的地选择，不同的学科分析可能需要不同的优化算法。例如遗传算法和模拟退火算法适用于离散空间的搜索。在上述协同优化模型中，学科级优化模型和系统级优化模型可以分别选用不同的优化算法进行计算，而不需要选用多目标优化算法。因此，该模型属于二级优化模型。

4 工程实例

以某集装箱船的艉部结构FR-10～FR+28（如图4所示）的多目标优化设计为例，对上述两种优化模型进行对比分析。

4.1 有限元模型

采用4节点板壳单元模拟板。在连接两个网格密度不同的区域时选用3节点板壳单元，同时确保疏密网格的过渡平滑。采用2节点梁单元模拟型材单元，并考虑偏心的影响[11]。采用2节点杆元模拟支柱。采用偏心质量单元模拟压载水舱水质量、舵叶质量和螺旋桨质量，同时考虑质量惯性矩。空船结构质量和舾装等非结构质量按肋位以密度定义的分布质量方式计入。节点总数为62 933个；单元总数为93 280个。在肋位FR+28处，采用固定端约束。

首先采用Fluent软件计算出脉动压力；然后再将其转换到结构有限元分析的计算模型中；最后，采用时域响应分析方法进行船体结构动力响应计算。使用Lanczos方法和模态参与因子提取技术，提取结构前三阶固有频率。

为了获得具体的最优解，而非Pareto集，在分析过程中两个目标函数的权重wii=1,（）2 取相同值。

图4 船艉结构有限元模型Fig.4 Finite element model of ship stern

4.2 优化设计

（1） 设计变量

在船艉结构有限元模型中，板材厚度和骨材型号共计50个参数。根据质量、固有频率、速度和加速度对设计变量的灵敏度计算结果[12]，从中选择了15个参数作为优化设计变量：A01、A02、A03、A04、A08、A13、A14、A17、A18、A19、A20、A21、A23、T02、T04，如表 1 所示。

（2）多目标优化设计

多目标优化算法为基于精英策略的非支配排序遗传算法（NSGA-II）。算法的参数设置为进化代数250，种群大小50，交叉概率0.9，变异概率0.1。

（3）多目标协同优化设计

自适应模拟退火算法ASA（Adaptive Simulated Annealing）是一种高效快速的全局优化算法，用以解决具有多峰和非光滑性的高难度非线性优化问题。ASA算法的优点是能够获得全局最优解而不是局部最优解、对初始条件的要求低、肯定收敛且收敛速度较快。因此，二级优化策略均由ASA构成，即学科级优化和系统级优化均采用ASA算法。

4.3 结果与分析

根据上述两种算法获得的设计变量和静、动力学响应最优解分别汇总于表1～2。优化前、后结构最大合速度与合加速度随时间的变化分别如图5（a）、（b）所示。优化后艉部结构（FR-10～FR+25）的应力分布如图6所示。

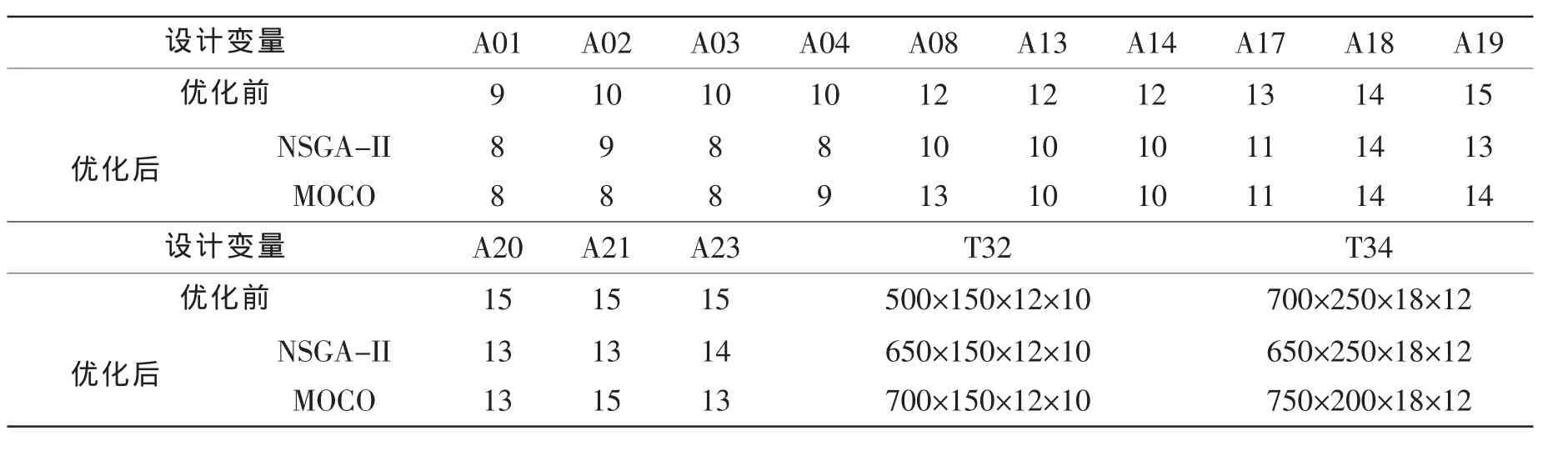
表1 优化前后不同优化方法下设计变量比较（单位：mm）Tab.1 Comparison of different algorithm between the initial and final design variables

表2 优化前后不同优化方法下设计响应比较Tab.2 Comparison of different algorithm between the initial and final design responses

表3 不同优化方法下最大应力比较（单位：MPa）Tab.3 Comparison of different algorithm between the initial and final maximum stresses

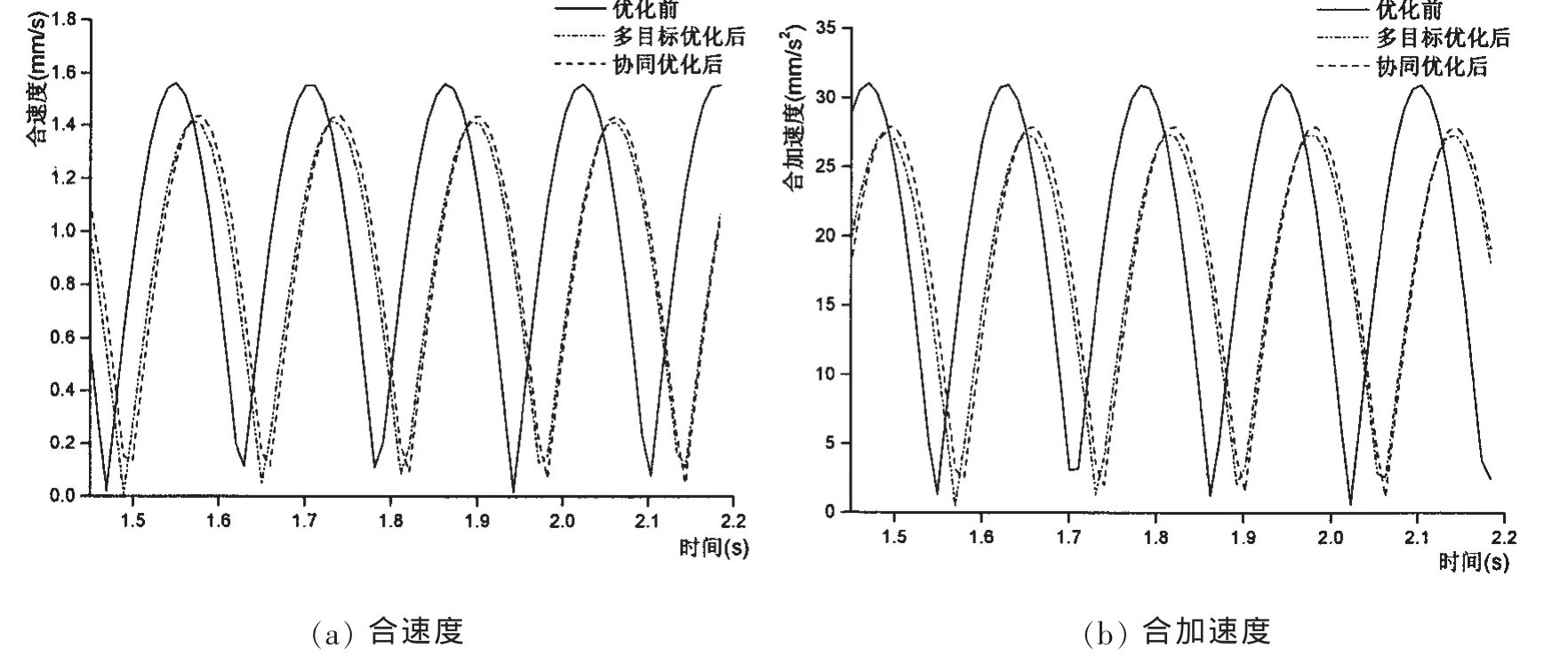
图5 不同优化方法下优化前后最大加速度曲线Fig.5 Comparison of different algorithm between the initial and final maximum acceleration

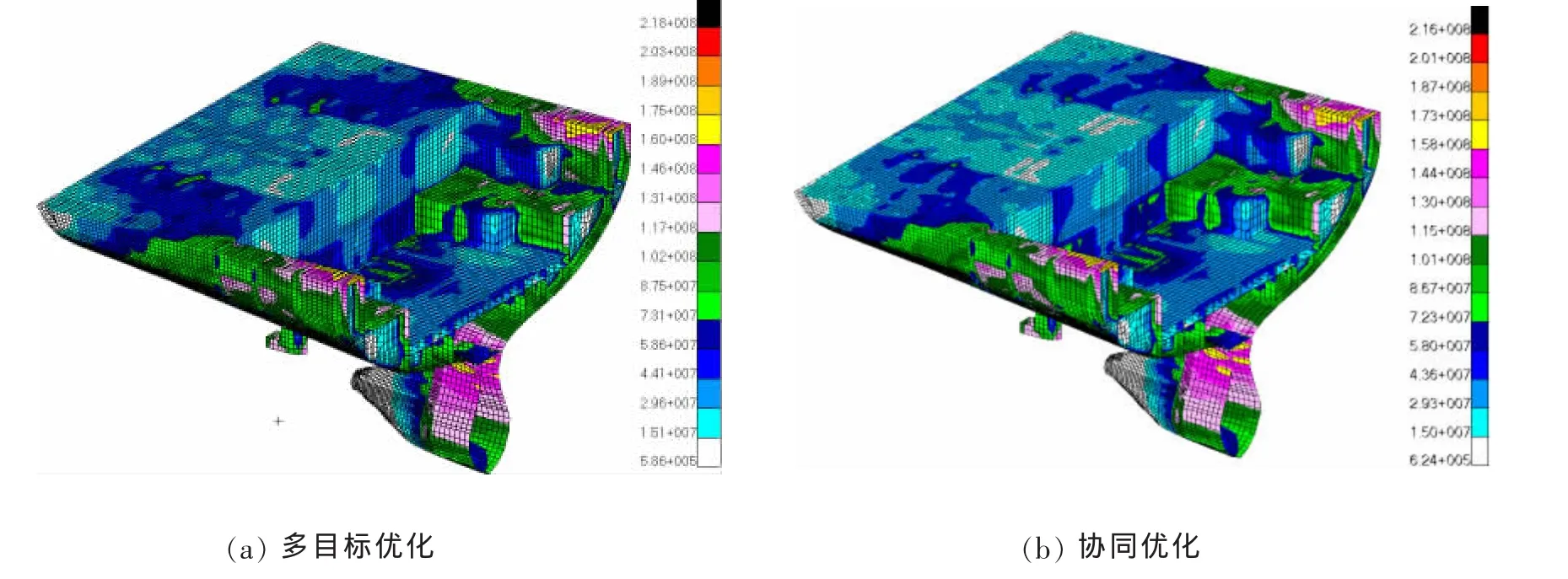
图6 不同优化方法下优化后艉部结构整体应力分布Fig.6 Comparison of stress distribution between the different algorithms

从上述结果可以看出：

（1）在对船体艉部结构进行设计优化时，两种算法的有限元模型、设计变量和初始点均相同。两种算法经过优化迭代后均获得了较为接近的最优解，达到预期目标。这也说明本文建立的基于NSGA-II算法的多目标优化模型和基于多学科优化技术的多目标协同优化模型是正确的、可行的，能应用于工程实际问题的设计优化中。其中，协同优化模型具有可根据学科特点和已有经验任意选择最佳优化算法的优点。

（2）相对于原结构质量，多目标优化和协同优化得到的最优结构质量均有大幅度下降，分别是6.47%和5.11%。在两种算法中，除设计变量A18保持不变之外，其余设计变量的取值均有不同程度的改变。这说明船体艉部结构在初始设计时考虑了一定的裕度。

（3）两种算法优化后的结构应力分布及其极值大小和z向最大位移基本接近，均充分发挥了材料的力学性能。

（4）优化后结构的前3阶固有频率均有所降低，但仍在频率禁区范围之外。协同优化后的结构第2阶固有频率储备（12.32%）高于多目标优化后的结构第2阶固有频率储备（12.05%）。通过优化，提高了结构抵抗共振的发生能力。

（5）优化后结构的动力响应也有较大幅度的改善。最大合速度数值的下降幅度均在8%以上，最大合加速度数值的下降幅度均在10%以上。根据商船振动评价基准（ISO6954）可知，优化后船体结构的动力响应位于振动轻微以下。

5 结 论

针对船体结构设计特点，论文建立了基于NSGA-II多目标遗传算法和多目标协同优化算法的船体结构多目标优化模型；以结构质量最小化和最大加速度最小化组成多目标函数，使用矩阵描述由板材厚度和骨材型号构成的离散设计变量集。以某集装箱船艉部结构为例，对其进行了结构静、动力性能的计算分析与优化设计。结果表明，优化后的艉部结构在一定程度上节省了工程原材料，大幅度降低了结构的动力响应，提高了固有频率储备，降低了发生共振的可能性；同时，仍然满足强度和刚度要求，达到了预期目标。

[1]Huang Haiyan,Wang Deyu.Multi-objective optimization of preliminary ship design[J].Journal of Ship Mechanics,2009,13(3):416-425.

[2]李学斌,朱学康.潜艇耐压圆柱壳的多目标优化设计[J].中国造船,2009,50(1):10-18.

[3]Coello C A.http://www.lania.mx/～ccoello/EMOO/EMOObib.html[J/OL].

[4]Ilan Kroo,Valerie Manning.Collaborative Optimization:Status and Directions[J].AIAA-2000-4721.

[5]黄海燕,王德禹.结构减振设计的协同优化分析[J].振动与冲击,2009,28(8):113-116.

[6]Alexandrov N M,Lewis R M.Analytical and computational aspects of collaborative optimization for multidisciplinary design[J].AIAA Journal,2002,40(2):301-309.

[7]Guan Ji,Lin G.Analysis and enhancement of collaborative optimization for multidisciplinary design[J].AIAA Journal,2004,42(2):348-360.

[8]陈建军,车建文,崔明涛,戴 君,马洪波.结构动力优化设计述评与展望[J].力学进展,2001,31(2):181-192.

[9]顾松年,徐 斌,荣 见,姜节胜.结构动力学设计优化方法的新进展[J].机械强度,2005,27(2):156-162.

[10]Huang Haiyan,Wang Deyu.Improvement of collaborative optimization[J].Journal of Shanghai Jiaotong University,2010,15(1):1-6.

[11]黄海燕,王德禹.加筋板结构的自由振动分析[J].船舶工程,2008,30(6):1-4.

[12]黄海燕,王德禹.基于灵敏度的多学科优化设计变量的模糊分析[J].上海交通大学学报,2009,43(8):14-18.

Multi-objective optimization of ship stern under static and seismic loading

HUANG Hai-yan1,LIN Zhi-xiang2,WANG De-yu3

(1 School of Naval Architecture and Ocean Engineering,Jiangsu University of Science and Technology,Zhenjiang 212003,China;2 School of Water Resources,Hydraulic Power and Architecture.Yunnan Agricultural University,Kunming 650201,China;3 State Key Laboratory of Ocean Engineering,Shanghai Jiao Tong University,Shanghai 200030,China)

The goal of this effort was to develop and compare two different multi-objective optimization models for the design of ship stern.They include the multi-objective optimization model based on the fast nondominated sorting genetic algorithm and the multi-objective collaborative optimization model based on the multidisciplinary analysis.The discrete design variable sets including the thickness of plate and the model number of beam are depicted with matrix.The objective functions are how to get the minimum structural mass in the static analysis and how to minimize the maximum acceleration of structure in the dynamic analysis.The proposed models were demonstrated with an optimization problem of container ship stern under static and seismic loading.The obtained optimal design indicates the great potential of decreasing structural mass and vibration level and increasing natural frequency reserve under the strength and stiffness requirements.The analysis progress and results show that the models are feasible and well-suited for using in actual optimization problems of ship design.

book=1271,ebook=116

multi-objective optimization;collaborative optimization;dynamic response;genetic algorithm;discrete design variable

U661.4 O327

A

1007-7294（2011）11-1270-08

2010-12-28 修改日期：2011-03-26

江苏省船舶先进设计制造重点实验室开放研究基金（No.CJ0805）；江苏省高校“青蓝工程”优秀青年骨干教师基金资助项目；江苏科技大学优秀青年骨干教师基金资助项目

黄海燕（1975-），男，博士，副教授，主要从事工程结构设计与断裂损伤分析，

E-mail:expressemail@126.com。