横向补给系统高架索的参激振动研究

何学军，张良欣，任爱娣

（海军工程大学 后勤指挥与工程系，天津 300450）

横向补给系统高架索的参激振动研究

何学军，张良欣，任爱娣

（海军工程大学 后勤指挥与工程系，天津 300450）

考虑了集中质量、轴向运动等因素对系统动力学行为的影响，建立了海上横向补给系统高架索的面内振动的连续模型。利用Galerkin方法对高架索偏微分模型进行模态离散，得到了1、2阶模态耦合的高架索系统的标准的动力学控制方程，利用多尺度方法对动力学方程进行渐近分析。对系统存在的两类参数激励共振进行了数值分析，得到了系统时间历程曲线、相图以及频谱图，研究结果表明高架索横向振动存在混沌等复杂的动力学特性。

参激振动；横向补给；高架索；Galerkin方法；混沌

张良欣（1965-），男，教授，博士生导师，博士。

1 引 言

由于横向干货补给过程中集中质量及高架索轴向运动的影响，使得横向补给系统高架索的动力学行为非常复杂。目前关于海上航行横向干货补给系统[1]的高架索研究的文献很少，高架索系统的非线性动力学研究尚属空白，高架索的动力学理论研究需借鉴类似连续结构的动力学研究成果。陈自力，唐驾时[2]建立了移动集中载荷作用下的悬索动力学简化模型，通过Galerkin方法和多尺度法对系统振动频率特性进行研究；陈立群等[3-4]考虑悬索本身的结构非线性因素的影响，对匀速、变速轴向运动弦线的横向振动的动力学行为及其控制进行了广泛深入研究；张伟[5]利用多尺度、正规形及数值方法对参数激励作用的轴向运动粘弹性传送带的Shilnikov形式的多脉冲和混沌行为进行研究；Lin和Perkins[6]建立了具有若干集中质量悬索的三自由度线性振动模型，提出了可用于求解任意垂度悬索特征解的半解析半数值的方法。Rega等[7-8]建立了无集中质量悬索控制方程，利用Galerkin方法、直接摄动法、数值方法以及几何方法，对小垂度限幅振动悬索的平面和空间运动非线性动力学行为进行了深入研究。上述研究对高架索动力学行为具有很好的参考价值，本文综合了上述文献的建模思想，将高架索简化为具有集中质量的轴向参激振动的悬索模型，基于弹性力学理论、非线性动力学理论，建立了高架索的面内振动理论模型。综合利用Galerkin方法和多尺度方法对系统进行了渐近分析，在分析过程中，考虑了低阶、高阶模态耦合效应。同时，利用数值方法对系统两种参激共振情况进行分析，研究结果表明系统存在复杂的混沌运动现象。

2 控制方程建立及简化

由弹性力学理论，静力作用下高架索变形为

其中：dx为高架索索单元的轴向静位移；dy为高架索索单元的横向静位移。

在静载荷和动载荷共同作用下，高架索的总变形为

式中：du1为高架索索单元的横向振动位移；du2为高架索索单元的轴向振动位移；他们不仅与时间有关，同时还与坐标位置有关，为du1（x,t）、du2（x,t）的简写形式。

（2）式移项并进行二阶泰勒展开，整理得

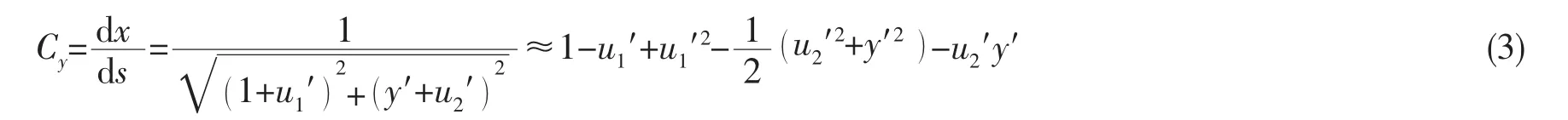
式中“′”表示对x求导。

结构动应变为

根据Hamilton变分原理[9]，得高架索面内振动控制方程为

式中：E为高架索弹性模量；A为高架索截面面积；M集中质量；δ（ x- xm）为Direc函数；xm为货物距高架索发送端水平距离；ρ为高架索密度；·表示对时间t求导；u2（xm,t）为集中质量的横向位移；v（t）高架索整体的轴向运动速度，与坐标位置无关，由v（t）=v0sin（ Ω1t）确定；xm为货物距高架索发送端水平距离。高架索空间形态如图1。

为了研究高架索横向振动，将高架索轴向运动作为激励简化高架索面内控制方程。考虑参激情况，根据边界条件u1（0,t）=0，u1（l,t）=lp（t ），p（t）为高架索右端相对于左端的无量纲轴向运动位移，为激励项。对方程（5a）分别进行边界积分[10]，忽略高阶小量u′2、y′2影响，整理得

图1 高架索空间形态图Fig.1 The schematic model of highline cable

将（6）式代入（5b）式，可得高架索横向振动控制方程

式中：p（t）=b0sin（ Ω2t），b0为无量纲常数。

3 渐近分析

利用Galerkin方法对方程（7）进行离散，令

将（8）式代入方程（7），根据模态正交性，得高架索1、2阶耦合模态振动的控制方程

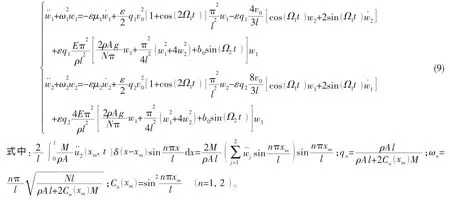
由多尺度法，令

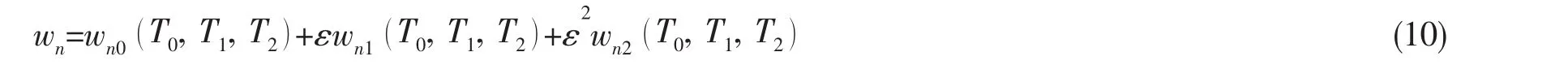
将（10）式代入方程（9），比较 ε 同幂次项系数，得：

Ω2=2ω2+εσ3情况，σ3为调谐函数，可确定系统 1、2 阶模态振动振幅 a1、a2表达式，如（16）式

4 数值分析

考虑 1：2 内共振（ω2≈2ω1），高架索轴向运动频率 Ω1≈ω1+ω2，系统参数取值如下：

l=40 m；E=1.8×1011Pa；ρ≈7 800 kg/m3；v0=3 m/s；xm=15 m；M=500 kg；N=20 kN；A=4.9×10-4m2（对应高架索直径25mm）；b0=0.005。

利用Mathematica程序对高架索横向振动动力学响应特性进行数值分析，同时利用FFT变换对系统进行频谱分析，得到上述参数情况下系统1、2阶模态振动的时间历程曲线、运动相图及频谱图，如图（2）、图（3）所示。

情况 1：Ω2≈2ω1参激共振情况

图2 高架索1阶模态振动时间历程曲线、相图以及频谱图（Ω2≈2ω1）Fig.2 Time flow,phase portrait and frequency spectrum of first model of highline cable

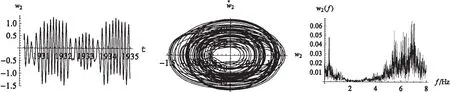
图3 高架索2阶模态振动时间历程曲线、相图以及频谱图（Ω2≈2ω1）Fig.3 Time flow,phase portrait and frequency spectrum of second model of highline cable

由图2可见，当Ω2≈2ω1（参数激励频率近似等于1阶模态频率2倍）时，系统的1阶模态振动频率相对简单，有几个主要峰值构成，为概周期运动；由图3可见，系统的2阶模态振动频率成分相对复杂，呈现连续性，由时间历程曲线、运动相图可见系统振动幅值变化剧烈，可以判断为混沌运动。

情况 2：Ω2≈2ω2参激共振情况

图4 高架索1阶模态振动时间历程曲线、相图以及频谱图（Ω2≈2ω2）Fig.4 Time flow,phase portrait and frequency spectrum of first model of highline cable

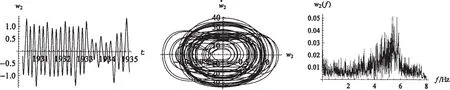
图5 高架索2阶模态振动时间历程曲线、相图以及频谱图（Ω2≈2ω2）Fig.5 Time flow,phase portrait and frequency spectrum of second model of highline cable

由图4、5可见，当Ω2≈2ω2（参数激励频率近似等于2阶模态频率2倍）时，系统的1阶模态振动频率比情况1要复杂得多，系统振幅值有大范围变化，此时系统的1阶模态振动具有典型的混沌运动特征；2阶模态振动频率成分尤其复杂，振幅存在明显的跳跃，具有典型的混沌运动特性。该情况下，系统模态振动幅值较情况1要小，故该类型的参激共振对高架索而言不如情况1危险。

5 结 论

（1）考虑集中质量、索端轴向运动等因素对高架索的影响，建立了海上航行横向干货补给系统的高架索面内振动的连续模型。

（2）考虑高架索低阶与高阶模态耦合作用，结合Galerkin离散与多尺度方法对系统进行渐近分析。考虑了模态间的内共振以及参数激励共振，对系统进行了详细的数值分析，研究结果表明高架索横向振动中存在复杂的混沌运动现象，参数激励频率对系统混沌运动特性影响较大。

[1]邓 凯,李红涛,余建星.高架索航行补给中船舶在波浪中的运动性能研究[J].船舶力学,2009,13(2):217-225.

Deng Kai,Li Hongtao,Yu Jianxing.Behaviour of ships in replenishment of highline system in waves[J].Journal of Ship Mechanics,2009,13(2):217-225.(in Chinese)

[2]陈自力,唐驾时,邓旻涯.集中荷载作用下悬索的自振频率分析[J].噪声与振动控制,2006,26(5):41-44.

Chen Zili,Tang Jiashi,Deng minya.The natural vibration frequency analysis of suspended cables under a concentrated load[J].Noise and Vibration Control,2006,26(5):41-44.(in Chinese)

[3]陈立群,丁 虎.轴向变速运动黏弹性梁稳态响应:近似分析及其数值验证[J].中国科学:G辑,2009,39(1):112-122.

Chen Liqun,Ding Hu.Steady state response of accelerating moving viscoelastic beam:approximate analysis and numerical confirmations[J].Science in China:Series G,2008,39(12):112-122

[4]Chen Liqun,Zhang Nenghui,Jean W Zu.Bifurcation and chaos of an axmoving viscoelastic beams with time-dependent speed[J].Journal of Sound and Vibration,2005,284(3-5):879-891.

[5]Zhang Wei,Yao Minghui.Multi-pulse orbits and chaotic dynamics in motion of parametrically excited viscoelastic moving belt[J].Chaos Solitons and Fractals,2006,28(1):42-66.

[6]Lin H P,Perkins N C.Free vibration of complex cable/mass systems:theory and experiment[J].Journal of Sound and Vibration,1995,179(1):131-149.

[7]Rega Giuseppe.Nonlinear vibrations of suspended cables-Part I:Modeling and analysis[J].American Society of Mechanical Engineers,2004,57(6):443-478.

[8]Benedettini F,Rega Giuseppe,Alaggio R.Non-linear oscillations of a four-degree-of-freedom model of a suspended cable under multiple internal resonance conditions[J].Journal of Sound and Vibration,1995,182(5):775-798.

[9]徐建平,桂子鹏.变分方法[M].上海:同济大学出版社,1999.

Xu Jianping,Gui Zipeng.Variational method[M].Shanghai:Tong Ji University Press,1999.(in Chinese)

[10]Nayfeh A H,Mook D T.Nonlinear oscillations[M].New York:Wiley-Interscience,1979.

Parametrically excited oscillation of highline cable of alongside replenishment

HE Xue-jun,ZHANG Liang-xin,REN Ai-di

(Department of Logistics Command and Engineering,Navy University of Engineering,Tianjin 300450,China)

A parmetrically excited oscillation continuum equation of highline cable of alongside replenishment system at sea was formulated by elastic mechanics,which considered the influence of the concentrate mass and the axial motion of the highline cable.The partial differential equation was discretized into ordinary differential equation by Galerkin method,the standard dynamic equation of highline cable was obtained by considering the coupling of different order models.The equation was asymptotically analysed by multi-scale method.Two kinds of parametrically excited resonance cases were analyzed numerically,and the time history curve,phase trajectory and frequency spectra were obtained.The results show that there are complex dynamics behavors such as chaos in parametrically excited oscillation of the highline cable.

parametrically excited oscillation;alongside replenishment;highline cable;Galerkin method;chaos

U661.4

A

1007-7294（2011）11-1283-07

2010-12-08 修改日期：2011-06-27基金项目：中国博士后科学基金资助项目（20080431381）；中国博士后科学基金特别资助项目（200902669）作者简介： 何学军（1978-），男，在站博士后，博士，E-mail:hexuejun@tju.edu.cn；