端部球面舱壁应力近似解
朱邦俊,王 丹,万正权
(中国船舶科学研究中心,江苏 无锡 214082)
端部球面舱壁应力近似解
朱邦俊,王 丹,万正权
(中国船舶科学研究中心,江苏 无锡 214082)
端部球面舱壁是一种组合回转壳结构,文章采用与回转壳相对应的弹性基础梁理论进行近似求解,考虑了厚薄板中曲面不一致引起的附加力矩和邻近肋骨的影响。该方法可应用于潜艇实际结构的设计计算。
端部球面舱壁;弹性基础梁;应力;位移
1 引 言
端部球面舱壁利用了球壳受力的优点,可以获得重量较轻而承载能力较大的效益,球面舱壁应是首选的结构形式。
球面舱壁一般由半径为R的球面壳、经线半径为r0的过渡短环壳及锥端半径为rB的圆锥壳三个部分组成,称之为三心球面舱壁或环球形舱壁,见图1。锥壳部分不一定是正圆锥,但在理论计算时都近似假定为正圆锥。于是,端部球面舱壁被视为轴对称回转壳。过渡环壳两侧结构主曲率发生突变而引起较大的经向(经线方向)弯曲,因此,过渡环壳的经向弯曲是舱壁强度计算的关键。环壳两端为光顺连接时,其最大经向弯曲一般在环壳中点;若环壳两侧不光顺连接,也可能出现在环壳两侧,在工程中应尽量采用光顺连接。在本文的计算方法中考虑了舱壁邻近肋骨以及环壳一侧厚、薄板连接处由于中曲面不一致引起的附加力矩的影响,使理论方法更加全面和完整。
2 基本假定与力学模型
2.1 基本假定
(1)端部球面舱壁为轴对称回转壳,忽略经向力引起的复杂弯曲;

式中:Fc为邻近肋骨剖面积,mm2;rc为 c节点处的锥端半径(见图 2),mm;Δc为 c节点处的垂向位移,mm。
(3)环壳与锥壳连接处厚、薄板中曲面不一致引起的附加力矩为mB;

式中:p为静水压力,MPa,rB为B节点处的锥端半径 (见图2),mm;φ3B为B节点处锥端第二主曲率半径ρθ3B与回转轴夹角,见图2;Δ为相邻厚、薄板中曲面之间的距离,mm;ε为考虑经向力偏心引起的力矩符号参数,当外表面重合时ε=-1,当中面重合时ε=0,当内表面重合时ε=1。
(4)以厚板削斜过渡的中心点作为厚、薄板连接的分界点。
2.2 力学模型
端部球面舱壁设定为由球面壳、过渡环壳和圆锥壳组合而成的轴对称回转壳体。在组合壳A、B、C三个节点处切开,将结构分解成四个部分,见图2。
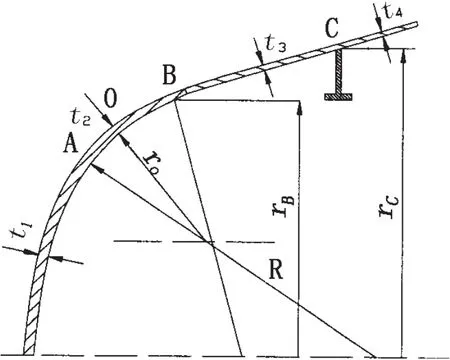
图1 端部球面舱壁结构Fig.1 The end spherical bulkhead

图2 端部球面舱壁结构分解及受力状态Fig.2 The analytical model of end spherical bulkhead
每部分结构除受均布水压力p作用外,结构在节点边界处承受边界力Q和弯矩M。考虑到公式推导和使用的普遍性,A、B节点两侧结构不作光顺连接的假定,即两侧结构在节点处的纬向曲率半径ρθ及其与回转轴的夹角φ不相等。C节点两侧锥壳一般为同一锥壳,考虑到可能出现两个不同的锥壳,也设定两锥在C节点处的ρθ及φ不相等。
对于球面壳和C节点右侧的长锥壳,它们在受均布水压力作用的同时,仅有一个边界承受边界载荷,应用弹性力学中的回转壳理论[2],是容易求解的。对于A、B节点之间的过渡环壳,其第二主曲率半径ρθ是变化的,因而壳体微分方程是变系数的,需应用渐近积分方法求解。过渡环壳一般都很短,从工程应用出发,根据环壳的力学特征,将环壳近似模拟成同时承受边界载荷和均布载荷q2作用的刚度系数为 Et2的弹性基础梁。载荷q2根据无矩状态环壳的实际位移来确定。同样,B、C节点之间的短锥壳模拟成同时承受边界载荷和均布载荷q3作用的刚度系数为Et3/的弹性基础梁,载荷q3根据无矩状态锥壳的实际位移来确定。
设定三个节点 A、B、C 的垂向位移和转角分别为 ΔA、ϑA,ΔB、ϑB,ΔC和 ϑC,共六个未知量;被分解的四部分结构,应用回转壳和弹性基础梁理论,可解得边界上的力Q和力矩M与相应位移Δ和转角ϑ的关系式;根据节点A、B、C处的力和力矩的平衡条件,可建立六个方程式;六个方程可求解六个未知量。
3 边界力与位移关系式
3.1 球面壳
根据回转壳理论,并对有关参数作适当换算[1],可解得

3.2 C节点右侧长锥壳
与球面壳一样,根据回转壳理论,并对有关参数作适当换算[1],可解得

3.3 A、B节点间的过渡环壳
根据有限长弹性基础梁理论可解得[1,3]
a.环壳左端

b.环壳右端

3.4 B、C节点间的短锥壳
与环壳类似,运用有限长弹性基础梁理论可解得
a.锥壳左端
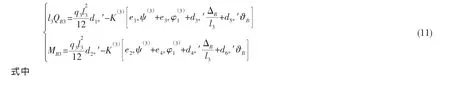
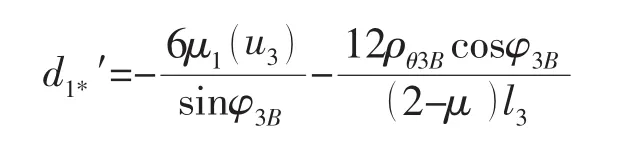
其余系数参照(8)式,只需替换式中相应参变数。
b.锥壳右端
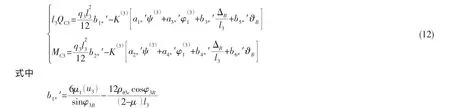
其余系数参照(10)式,只需替换式中相应的参变数。
4 问题求解
4.1 节点C的平衡条件

将(5)式、(12)式和(1)式相应项表达式代入(13)式并注意

以及q3=q4,可以解得

4.2 节点B的平衡条件

将(9)式、(11)式及(2)式和(15)式相应项表达式代入(18)式并注意

可以解得

4.3 节点A的平衡条件

将(3)式、(7)式相应项代入(24)式并注意(20)式可解得

由(25)式求出 ΔA、ϑA以后,根据前面的相关公式,很容易求得 ΔB、ϑB,ΔC、ϑC;以及各部分结构在节点处的边界力和力矩,即 QA1、QA2、MA1、MA2、QB2、QB3、MB2、MB3、QC3、QC4、MC3、MC4、QC3、QC4、MC3和 MC4。
4.4 环壳中点的位移和力矩
环壳中点的经向总应力一般被视为最大(接近最大)应力,为了计算环壳中点的应力,必须计算环壳中点的位移和经向弯矩。
在环壳的求解中是将环壳简化为两端边缘承受边界力和力矩并承受均布载荷q2作用的弹性基础梁,具体求解详见文献[1,3]。
(1)环壳中点位移
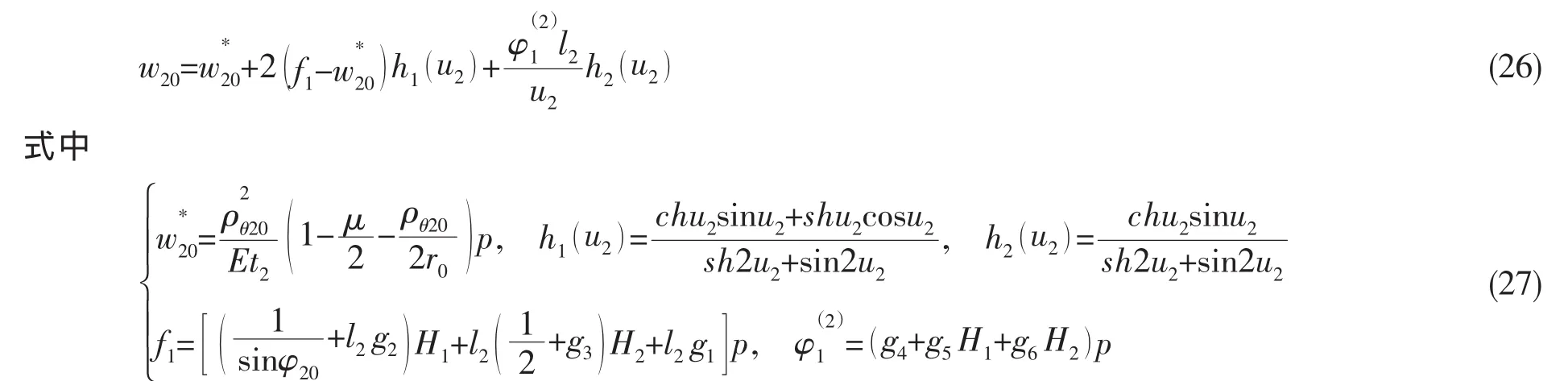
(2)环壳中点的经向弯矩
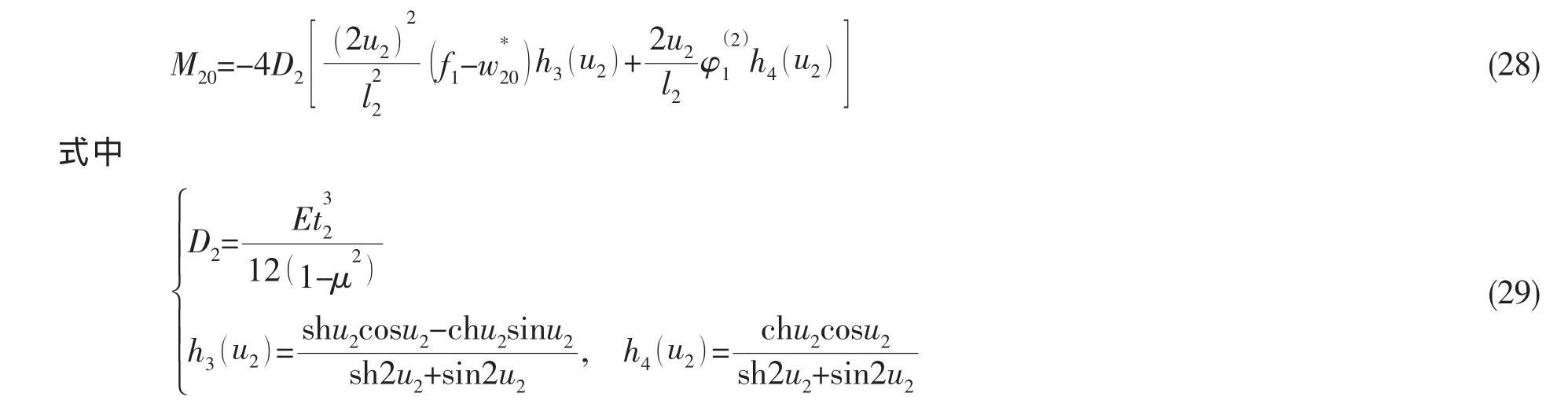
5 端部球面舱壁应力计算
在工程设计中,人们所关心的主要是球面壳的膜应力;环壳中点的经向总应力;环壳与锥壳连接处(B节点)锥壳一侧船体壳板的经向总应力;环壳与球面壳连接处(A节点)球面壳一侧的经向总应力等。
5.1 球面壳膜应力
在外水压力作用下,球面壳的膜应力为

5.2 环壳中点的应力
(1)环壳中点的经向总应力
在环壳求解中,忽略了经向膜力对弯曲的影响,但在计算经向总应力时,应叠加由经向膜力产生的经向膜应力,即

式中 M20由(28)式计算。
(2)环壳中点的纬向总应力
环壳中点的纬向总应力为

式中 w20由(26)式计算,σs0由(31)式计算所得。
5.3 环壳与锥壳连接处锥壳一侧船体壳板应力
(1)B节点锥壳一侧船体壳板经向总应力为

其中:QB3、MB3由(11)式确定;t3*为建议取厚板削斜中心点厚度,无削斜时取 t3。
(2)B节点锥壳一侧船体壳板纬向总应力为

式中 ΔB由(19)式计算,σsB3由(33)式计算所得。
6 典型算例
本算例结构尺寸取自文献[1]并与文献列出的两种方法的计算结果列于表1。

表1 典型算例计算结果比较Tab.1 The comparison of calculation results for typical structure
分析表中数据可知,本文计算结果与文献中列出的结果相当一致,尤其与较为精确的渐近积分数值解更吻合,可用于工程设计。
7 结 语
(1)本文计算方法考虑了舱壁邻近肋骨以及环壳一侧厚、薄板连接处由于中曲面不一致引起的附加力矩的影响,使其力学模型更接近实际结构,完善了理论分析;
(2)文中对于过渡环壳选配适当的刚度系数、载荷和独立变量,将变系数的原始方程化解为弹性基础梁弯曲的常系数型微分方程,对于相对短的(沿经线)环壳而言,这样的转化和渐近积分的相对误差不大;
(3)环壳两端为光顺连接时,其最大经向弯曲一般在环壳中点,由表中计算结果可知,环壳构件最大应力可以近似地用中点应力来描述,较渐近积分而言更为方便、简捷;
综上所述,本文采用弹性基础梁理论对端部球面舱壁结构进行理论分析的思路对于解决潜艇复杂结构的工程实际问题是适用的。
[1]朱邦俊,王永军.潜艇端部球面舱壁应力计算的一种近似方法[R].无锡:CSSRC科技报告(03577),2003.
[2]诺沃日洛夫 B B.薄壳理论[M].北京:科学出版社,1959.
[3]朱邦俊,等.潜艇横向刚性构架区域应力计算解析方法[J].船舶力学,2005,9(5):109-114.
An analytical solution for stresses of the end spherical bulkhead
ZHU Bang-jun,WANG Dan,WAN Zheng-quan
(China Ship Scientific Research Center,Wuxi 214082,China)
Based on the theory of elastic foundation beam,an analytical method for stresses of the end spherical bulkhead is developed.The effects of additional bending moment are accounted for in the present method due to the adjacent ring-stiffener of pressure hull and the mismatch of mid-section between the thick and thin plates.The numerical results show that this method can be used in the design and calculation of submersible pressure hull.
end spherical bulkhead;elastic foundation beam;stress;displacement
U661.43
A
1007-7294(2011)11-1255-09
2011-08-28
朱邦俊(1938-),男,中国船舶科学研究中心研究员。

