基于距离单元统计模型的ISAR包络对齐方法

林玉川 陈卫东

(中国科学技术大学 合肥 230027)

1 引言

逆合成孔径雷达(Inverse synthetic aperture radar，ISAR)对空间非合作运动目标成像具有全天候、全天时的特点，是当前空间空天目标观测和目标识别的重要手段，在军用和民用领域具有重要的应用价值［1］。

众所周知，目标相对于雷达的运动可分解为平动分量和转动分量，ISAR成像通过对平动分量的精确补偿，利用等效转动分量进行成像。一般的平动补偿都包括包络对齐和初相校正两个基本步骤［2］，其中包络对齐用于消除目标平动造成的雷达回波在距离向上的错位，是进行初相校正和消除其他ISAR成像散焦因素的前提，包络对齐性能将直接影响ISAR成像质量。

自ISAR成像技术提出以来，相继出现了许多包络对齐方法，其中利用回波间相似性的包络对齐方法应用最为广泛，包络相关法［2］、包络最小熵法［3］是其最具代表性的两种方法。包络相关法通过计算相邻两包络的相关系数最大值对应的位置估计出距离向偏移量进行包络对齐。而包络最小熵法通过搜索使相邻两回波包络之和熵值最小的距离偏移量来完成包络对齐。研究表明包络最小熵法比包络相关法具有更好的对齐效果。

本文提出了一种基于距离单元统计模型的包络对齐方法。该方法包括两个步骤:首先利用已完成包络对齐的回波对距离单元统计模型参数进行估计;然后通过搜索使回波包络与距离单元统计模型最为符合的距离偏移量来完成包络对齐。显然建立距离单元统计模型是实现该包络对齐方法的前提和关键，本文首先对此进行了详细分析。本文研究还表明包络相关法是该方法的一个特例。

仿真实验就包络相关法、包络最小熵法和本文方法的包络对齐性能进行了对比分析，验证了本文方法的有效性。

2 距离单元统计模型

2.1 目标回波模型

考虑线性调频信号(LFM)，设雷达发射信号为:

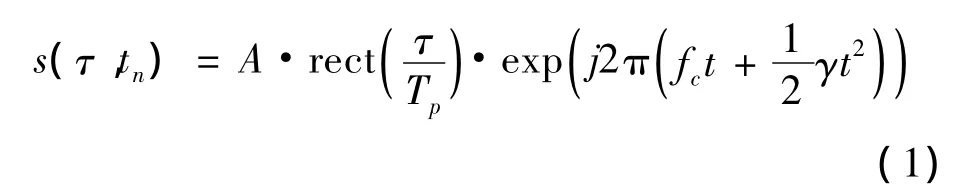
其中tn为脉冲发射时刻，即慢时间;τ为以tn为起点的快时间;fc为中心频率;Tp为脉宽;γ为调频率，则Δf= γTp为信号带宽

假设目标由L个散射点构成，εl、分别为第l个散射点的散射系数及在慢时间tn与雷达的径向距离，则目标在差频域回波为．［1］:

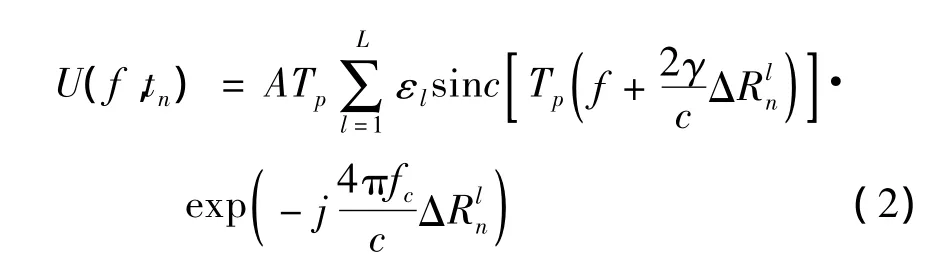
式(2)中的目标回波是各散射点回波的矢量和。该回波还可以通过下述方式获得:先把同相位的散射点回波进行矢量合成得到子回波;再将各子回波进行矢量合成得到目标回波。由于同相位回波在矢量合成时具有幅度相加相位不变的特性，因而上述目标回波获取方式有助于分析目标平动和转动对回波包络的影响。下面将分析采用该方式获取目标回波的表达式。

为了论述的方便，用集合D={Dl|l=1，2，…，L}来描述目标的散射点，其中Dl表示第l个散射点。散射点Dl的相位为，该相位一定处于某个区间，其中k为任意整数，记为k∈Z，H为一正整数，h=0，1，2，…，H- 1。 此 时内，其中将满足条件的所有散射点构造为集合，则可以得到目标散射点集的一个划分。基于该划分，式(2)可写成如下形式:

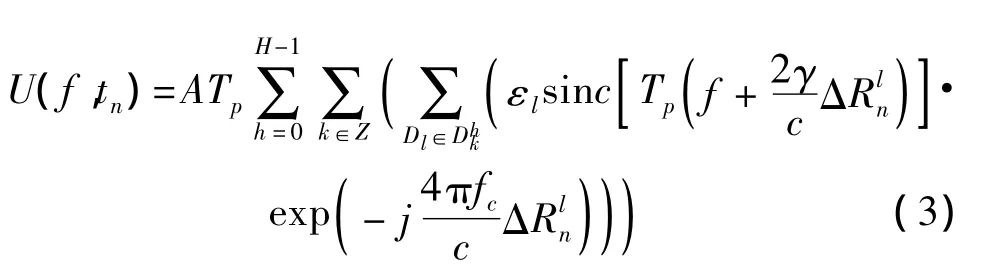
基于式(3)、(4)，可以将目标在差频域回波表示为如下形式:

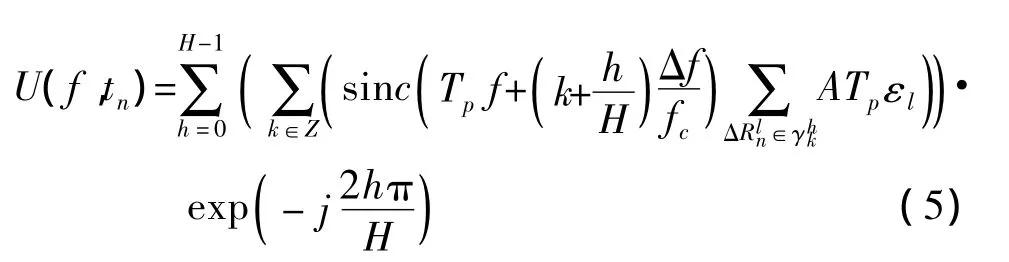
2.2 目标平动对距离像的影响

考察慢时间tq-1到tq的目标平动。设目标的径向平动距离为RΔ，由于目标平动散射点集将变为，则成立如下关系式:

目标平动将导致目标差频域回波的平移，其平移量可由相干差频公式计算．［1］:

因而将回波U(f，tq-1)在差频域平移fRΔ得到的U(f+fRΔ，tq-1)与 U(f，tq)是包络对齐的。由式(5)可得到:

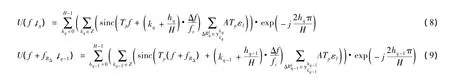
由于 Dhq-1kq-1与 Dhqkq包含相同的散射点，因而下式成立:

应用式(6)、(7)，可以证明:

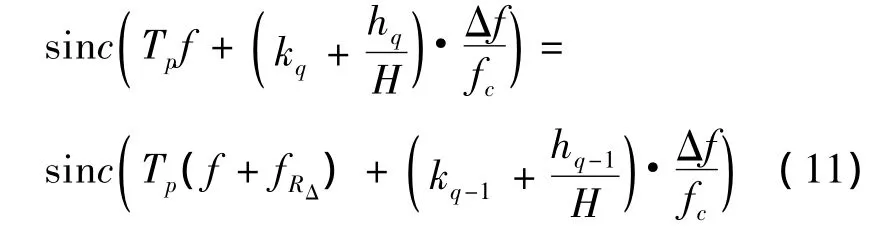
由式(10)、(11)可得:

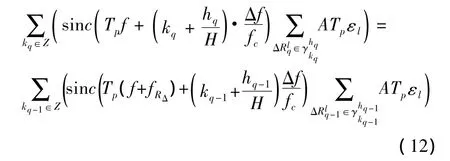
综合式(8)、(9)、(12)可以得出如下结论:若目标仅存在平动分量，对目标回波完成包络对齐后，H个子回波幅度不变，仅相位发生了变化。因而完成理想包络对齐的回波U(f，tn)可以表示为:

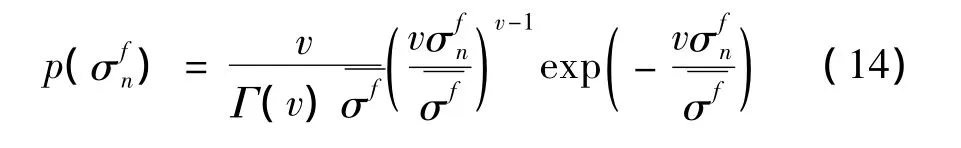
以(15)为基础容易得到:对于完成理想包络对齐的一维距离像Afn，其概率密度函数为［5］:

2.3 目标转动对距离像的影响

3 基于距离单元统计特性模型的包络对齐方法

实际的包络对齐过程都是对离散回波数据的处理。设 Sn= ［S(1，n)，S(2，n)，…，S(M，n)］是对的等间隔采样，样本长度为M。则对连续接收的N个回波，可得到离散回波包络矩阵…］，其中为Sn的转置。完成理想包络对齐后，离散化的距离单元统计模型可在式(16)的基础上得到:

3.1 距离单元统计特性模型的参数估计

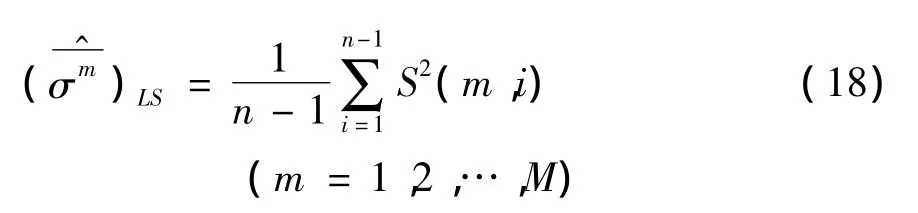
3.2 回波的距离偏移量估计

Sn包络对齐的结果为Sn的某个循环位移。令为Sn的一个循环移位，其中，则 Sn的所有循环移位构成集合。在中找到与距离单元统计模型最符合的元素便得到了Sn的距离偏移量v。

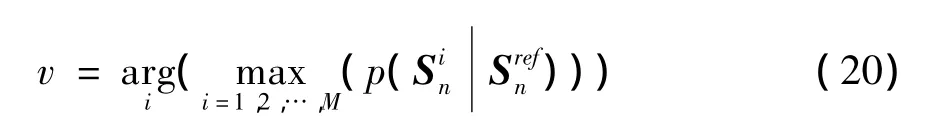
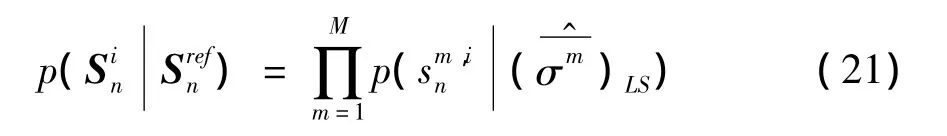
由式(17)～(21)，可以得到:

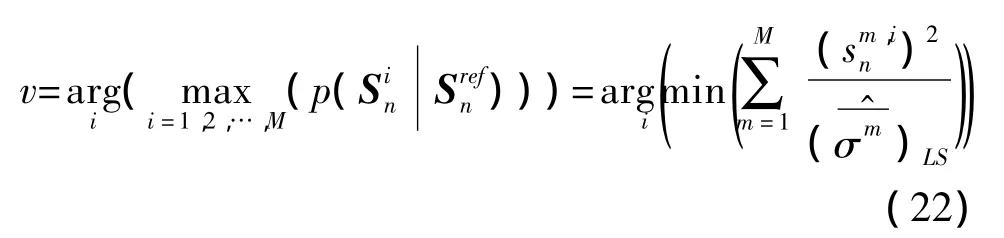
若 Un= ［U(1，n)U(2，n)…U(M，n)］为回波包络对应的回波Sn的采样，则对Un进行距离偏移v，就完成了回波Un的包络对齐。

至此，基于距离单元统计模型，通过距离单元统计特性模型的参数估计、回波的距离偏移量估计两个步骤，完成了一个完整的基于距离单元统计特性模型的包络对齐过程。

3.3 包络相关法的新解释

若理想包络对齐后，离散化的距离单元统计模型不是用式(17)来描述，而是用高斯分布来描述，即:

其中μm、ρm为S(m，n)的期望值和标准差。μm的最小二乘估计为:

由式(23)、(24)、(25)可得距离偏移量v为:

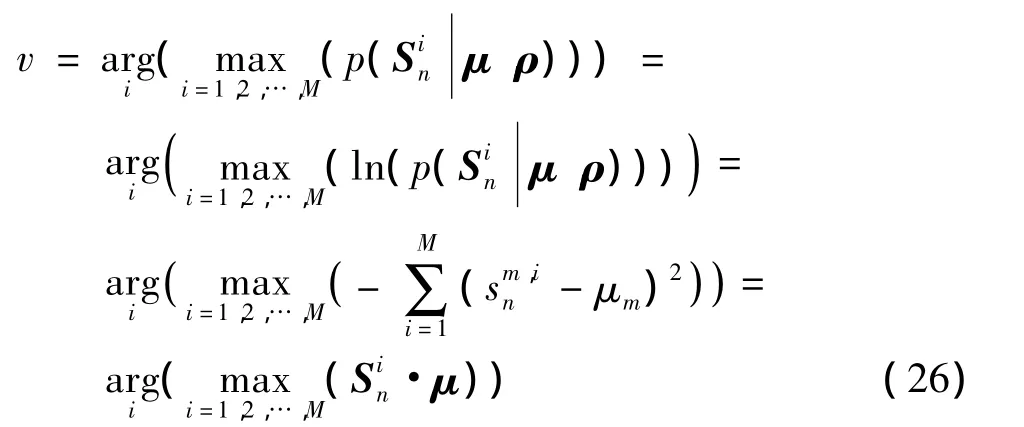
上述分析表明包络相关法是本文的包络对齐方法的一个特例。从距离单元统计模型的建立过程不难看出，本文建立的统计模型(17)比包络相关法采用的高斯分布模型在描述距离单元统计特性时更为准确，因而可以推断本文提出的方法比包络相关法应有更好的包络对齐效果。

4 仿真实验

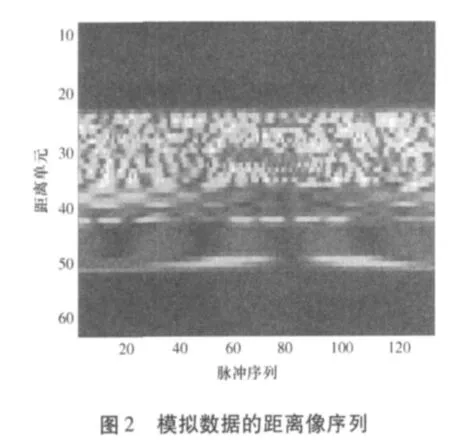
本文方法是基于线性调频信号的分析，但同样也适用于步进频率信号，这是由二者实现ISAR成像的原理决定的［7］。因此本文仿真实验选用 Dr.Victor C.Chen提供的MIG-25(图1给出了MIG-25的点模型示意图)模拟数据［8］，该数据采用步进频率信号，中心频率9GHz，带宽512MHz，共512个脉冲串序列，每个脉冲序列64个脉冲采样。图2给出该模拟数据的距离像序列。由于该数据给出了完成平动补偿的距离像序列，为比较包络对齐算法的对齐效果提供了参照标准。

为考察噪声对包络对齐性能的影响，将模拟数据转换为时域回波，加入-20dB～20dB间隔为2dB的高斯噪声后再转换为距离像序列。在每个信噪比点进行1000次Monte-Carlo试验。第a个信噪比点第b次试验的过程如下:对每个回波加入随机偏移，取en为整数使仿真在差频域完成，合理简化仿真过程;emax可以取较小值，因为使用质心法［9］先做一次包络对齐能够将距离偏移限制在较小范围，本文取emax=4)，得到随机偏移序列。完成包络对齐得到包络位移值序列Wt;记=E+Wt，则表征对齐结果与原始回波的距离偏差的众数MODE)表征回波的整体距离偏移。定义表示第a个信噪比点的包络对齐平均偏差，因而μa反映了包络对齐效果，μa越小包络对齐效果越好。

图3给出了包络相关法、包络最小熵法及新的包络对齐方法的在各信噪比时的包络对齐平均偏差。图3表明本文提出的新方法对齐效果优于包络相关法及包络最小熵法。仿真实验中，要达到相同的包络对齐效果，新的包络对齐方法比包络最小熵法的信噪比要求低2dB左右。

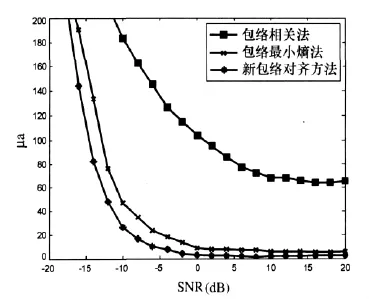
图3 三种包络对齐方法的包络对齐平均偏差

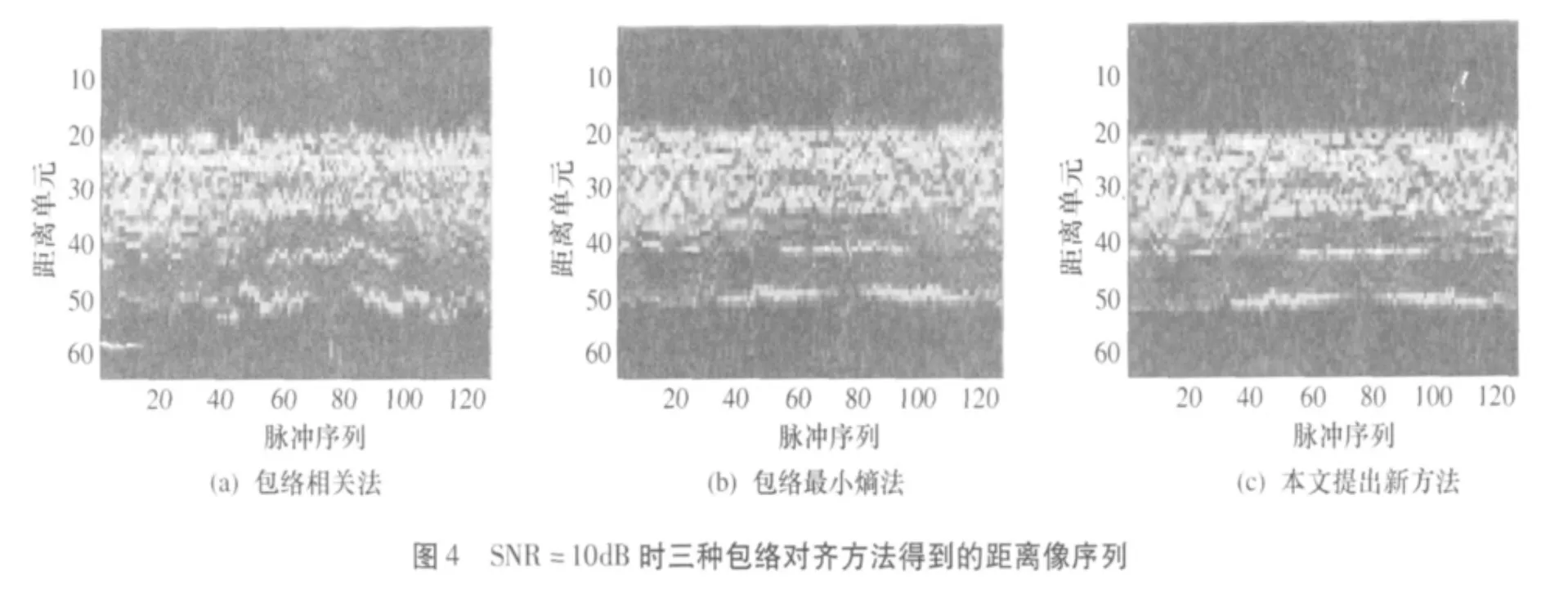
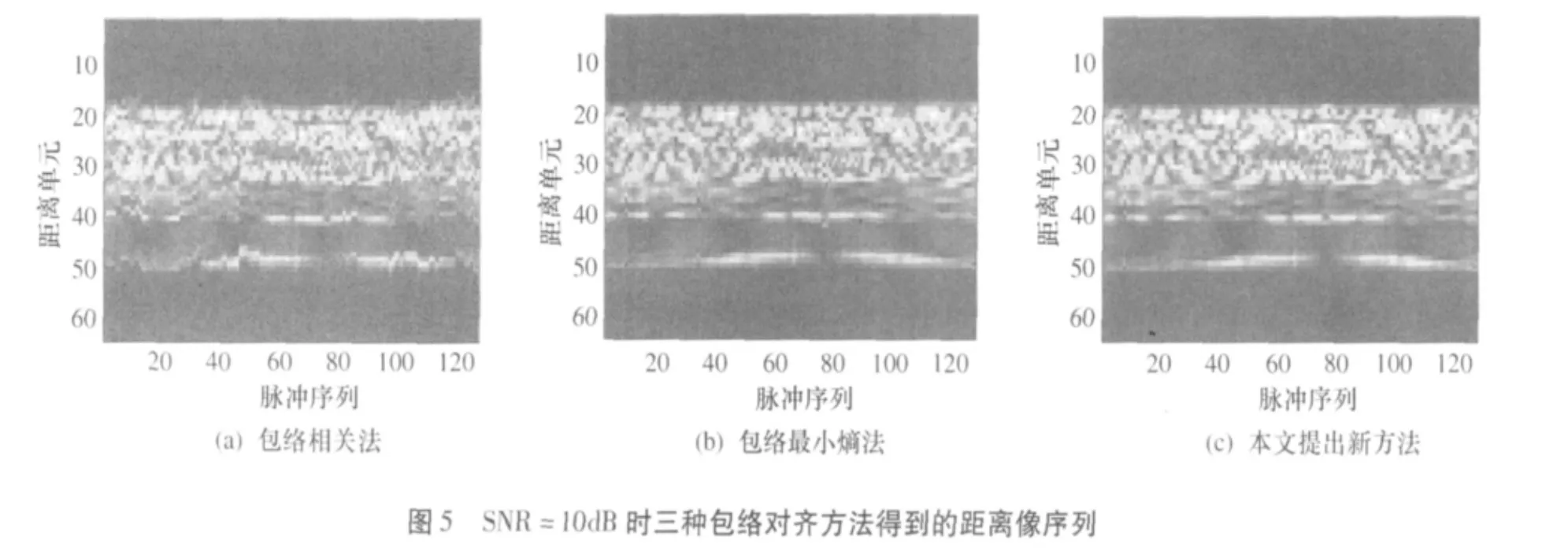
图4 、图5分别给出了信噪比为10dB和-10dB时某次Monte-Carlo试验中三种包络对齐方法得到的距离像序列，两图比较直观地反映出本文提出的包络对齐方法有更好的包络对齐性能。

5 结论

本文提出了一种基于距离单元统计特性模型的包络对齐方法，分析表明包络相关法是该方法的一个特例，理论上分析本文提出的方法比包络相关法有更好的包络对齐效果。仿真结果表明新的包络对齐方法比包络相关法和包络最小熵法有更好的对齐效果。

［1］保铮，邢孟道，王彤.雷达成像技术［M］.北京:电子工业出版社，2005.

［2］Chen Chung-Ching，Andrews Harry C.Target-Motion-Induced RadarImaging［J］.IEEE Transactions on Aerospace and Electronic Systems，1980，16(1):2-14.

［3］Wang Genyuan，Bao Zheng.The minimum entropy criterion of range alignment in ISAR motion compensation［A］.Radar 97(Conf.Publ.No.449)［C］，1997，236-239.

［4］Meyer Daniel P，Mayer Herbert A.Radar target detection:handbook of theoryand practice［M］.New York:Academic Press，1973.

［5］Ziemer Rodger E，Tranter William H.通信原理:系统、调制与噪声［M］.北京:高等教育出版社，2003.

［6］Kay Steven M.统计信号处理基础［M］.北京:电子工业出版社，2003，08.

［7］Wehner Donald R.High resolution radar［M］.Boston-London:Artech House，1987.

［8］Chen Victor C，Ling Hao.Time-frequency transforms for radar imaging and signal analysis［M］.Boston-London:Artech House，2002.

［9］毛引芳，吴一戎，张永军等.以散射质心为基准的ISAR成象的运动补偿［J］.电子科学学刊，1992，14:5.