超高速碰撞相似律的数值模拟验证*

沈雁鸣，陈坚强

（中国空气动力研究与发展中心，四川绵阳 621000）

在实验研究中，通常使用轻气炮、电磁炮或者爆炸加速器等加速器设备［1］，使金属弹体获得超高速度。这些设备体积庞大、费用昂贵、辅助设备繁杂、设计建设要求高，而且往往具有一定的速度极限，因此在很多时候无法满足实验要求。同时，金属弹体所用材料屈服极限高、流动性较差，实验中不好观测变形过程。而非金属材料如橡皮泥、石蜡等屈服极限低、流动性好、便于观察变形情况，并且成本低廉，容易压制成形，又可反复回收利用，是较为理想的进行超高速碰撞的模拟材料。

关于非金属材料对金属弹靶超高速碰撞的相似模拟，W.Johnson等［2］、J.Carrel等［3］对此进行过论证，马晓青［4-5］曾经对橡皮泥平头长杆弹撞击厚靶板的实验进行了研究，以模拟钢质长杆弹对厚靶板的撞击，取得了令人满意的结果。谈庆明［6-7］也曾对冲击相似律问题进行了详细分析和讨论。根据冲击相似律理论，可以把橡皮泥、石蜡等材料制成与金属弹体相同的弹体形状，以一定的速度进行碰撞实验，用以模拟相对应的金属超高速碰撞问题。

本文中，对超高速碰撞相似律进行详细理论推导及分析，得到量纲一化的相似律函数，然后根据相似律函数选择两种相似模型，利用改进的光滑粒子动力学方法对不同类型的超高速碰撞进行数值模拟。

1 超高速碰撞相似律

固体材料在超高速碰撞过程中所产生的冲击压力远大于它们的屈服强度。在此类碰撞过程的最初阶段，碰撞固体的性态类似于可压缩流体，弹体和靶体都将呈现出流动状态。因此，在模拟动态响应时除了考虑材料的力学性能，还必须考虑材料的流体动力学特性及其他相关系数［4，6］。主要有下面3类因素:（1）几何因素，如弹体靶体的尺寸、形状等参数（Lp1，Lt1，…，Lpn，Ltn）;（2）碰撞因素，如碰撞角度、速度和压力等参数（φ，vp，pp，pt）;（3）材料物理因素，如密度、模量、强度、温度、声速和比热等参数（ρp，ρt，Ep，Et，Yp，Yt，Tp，Tt，cp，ct，cV，p，cV，t）。

因此厚板开坑直径、侵彻深度或薄板穿透直径等尺寸应为上述参数的函数，有

使用量纲分析方法对式（1）进行简化，可取弹体尺寸Lp1、速度vp、温度Tp以及屈服强度Yt为基本量，可以得到下面的量纲一函数关系

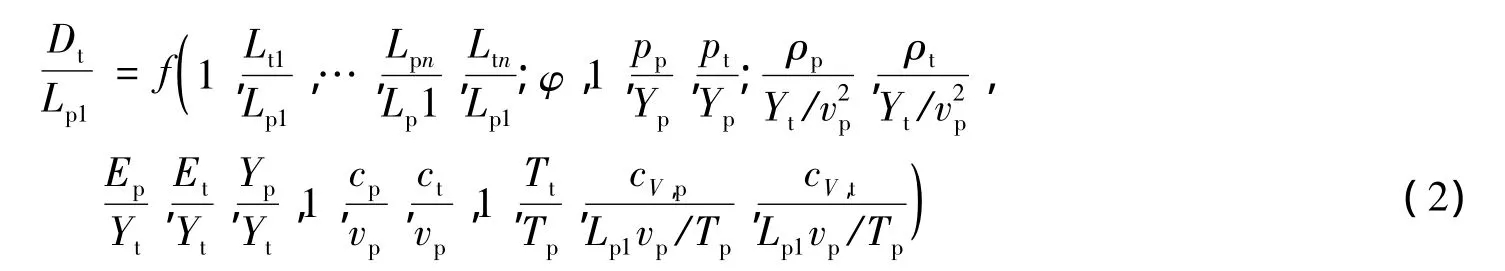
认为弹体和靶板初始温度相同，忽略碰撞过程热效应及超高速碰撞下材料的初始压力与弹性效应，

则式（2）可以变为

当模拟弹靶的几何形状与原弹靶相同，碰撞姿态也相同时，碰撞结果只与5个参数有关

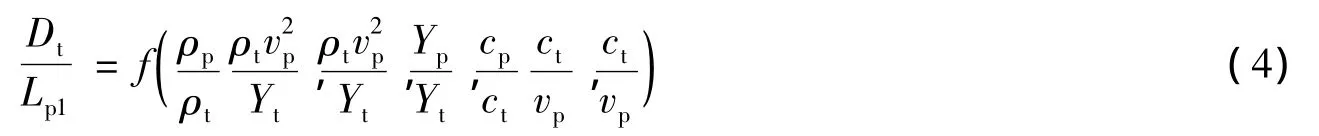
消去同类项，最后可以得到

第1个参数为材料密度之比。第2个参数与材料密度、碰撞速度及材料动态屈服强度有关，一般称为材料的破坏数，表征动压与强度之比，或惯性与强度性质之比。第3个参数为材料屈服强度之比。第4个参数为材料可压缩性之比，第5个参数为马赫数，表征惯性与可压缩性之比。当弹靶材料一致时，式（5）中的第1、3～4个参数都等于1。

张庆明在文献［1］中曾列举了许多关于超高速碰撞厚板开坑以及薄板穿孔研究得到的经验公式。其中，根据实验数据拟合所得的厚板开坑坑深表达式比较出名的有2/3次律

与此类似的，还有W.Herrmann根据实验拟合得到的公式［1］

式中:Ht为布氏硬度，近似认为Ht=3.6St=2.4Yt。

Sedgwick的计算则给出了上述各参数比较全面的结果［1］

在薄板穿孔实验中，考虑惯性和材料强度等影响，拟合得到孔径表达式为［1］

也符合量纲一函数关系式（5）推导所得。

例如，选用橡皮泥作为模型模拟硬钢弹靶间超高速碰撞。橡皮泥材料参数为=1 800 kg/m3，=3 MPa;硬钢的材料参数为=7 890 kg/m3，=600 MPa，代入式（10）可得模拟速度

即橡皮泥以0.3～1.5 km/s的速度即可模拟硬钢弹靶间2～10 km/s的超高速碰撞。

当弹靶材料各不相同时，超高速碰撞相似律同样适用。碰撞模型只要满足式（6）中3个参数相等的条件，碰撞结果应当相似。即必须同时满足以下3个关系

例如，以钨质穿甲弹穿透薄钢板为例，选用橡皮泥作为钨质穿甲弹的模拟材料。根据表1中几种材料参数，可以计算得到薄钢板的对应的模拟材料参数:ρ=738.5 kg/m3，Yp1=1 MPa，该材料密度和屈服强度都略低于石蜡，可通过一定的化学工艺获得。

表1 材料参数Table 1 Properties of materials

2 结果分析

针对上面的理论推导，结合工程实际，使用光滑粒子法对钨质弹体穿透薄钢防护板高速碰撞过程进行模拟。为了评估相似律的准确性，也对同模型的橡皮泥对材料甲防护板的碰撞进行计算，最后对结果进行比较分析。

2.1 钢弹撞击厚钢板

计算模型如下:弹体直径0.5 cm，直径采用16个粒子离散。靶板长10 cm，厚5 cm，分别采用320个粒子和160个粒子进行离散，由于对称性，只取其中1/2模型进行计算，总粒子数为25 385。粒子间距 Δx为312.5 μm，光滑长度h都为1.5Δx，材料参数见表1。

图1 石蜡碰撞石蜡板后变形Fig.1 Material deformation when paraffin projectile impacting onto thick paraffin target at v=0.32 km/s

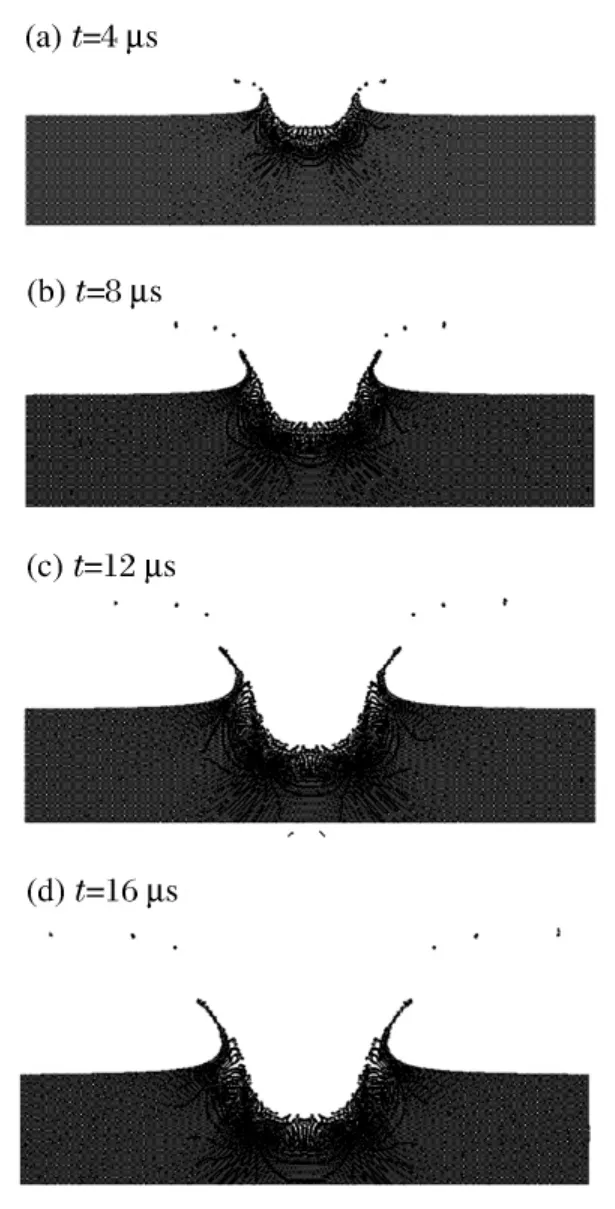
图2 硬钢弹碰撞硬钢板后变形Fig.2 Material deformation when steel projectile impacting onto thick steel target at v=2 km/s

图1～2是石蜡弹以0.32 km/s速度垂直击中同材质厚靶板和钢弹以2 km/s速度穿透薄钢板不同时间计算结果比较。碰撞后靶板迅速凹陷，凹陷最初弹坑直径远大于深度，冲击波朝外迅速传播。随着时间增加，弹坑从碰撞点朝外扩张，逐渐呈现半球形，扩张速度逐渐减小直至静止。弹体碰撞后则迅速变扁并破碎，破碎粒子平铺在弹坑中。弹坑周围出现“反唇”现象，靶板破碎粒子从坑内朝外喷射，变形停止后弹坑两端出现明显隆起。比较发现，两种计算模型碰撞后的开坑过程基本相同，同时二者相对应时间内靶板开坑形状与尺寸基本一致。

图3是两种模型在碰撞相似律准则下不同速度碰撞后靶板弹坑半径和弹坑深度比较。不难看出，硬钢和橡皮泥在超高速碰撞相似律对应的不同碰撞速度下，二者在弹坑尺寸的计算结果十分接近，误差在很小的范围内。由此也说明，在满足一定相似律条件下，可以使用石蜡模拟硬钢弹靶间的高速碰撞和超高速碰撞。

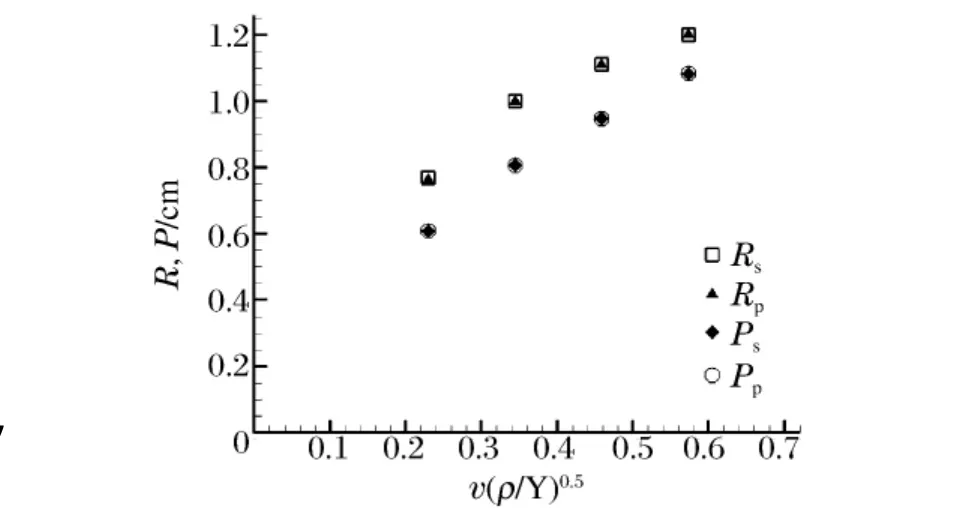
图3 石蜡和硬钢不同速度下开坑尺寸大小比较Fig.3 Crater final radius and depth versus impact velocity in paraffin impacting and steel impacting

2.2 钨弹斜穿透薄钢板

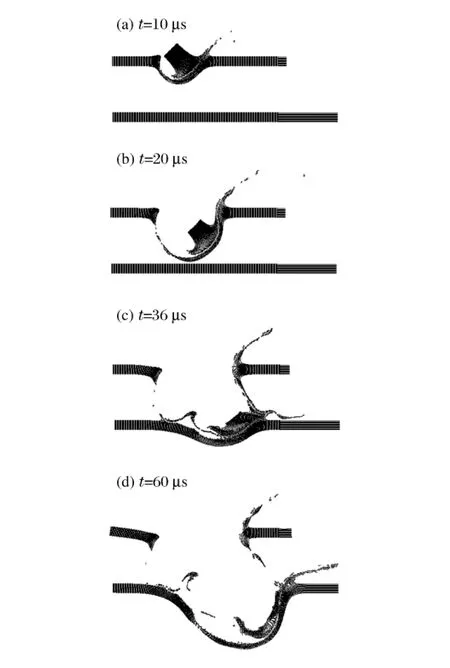
图4 钨弹斜撞击两层薄钢板后变形Fig.4 Material deformation when tungsten projectile impacting onto thin steel target at v=2.0 km/s

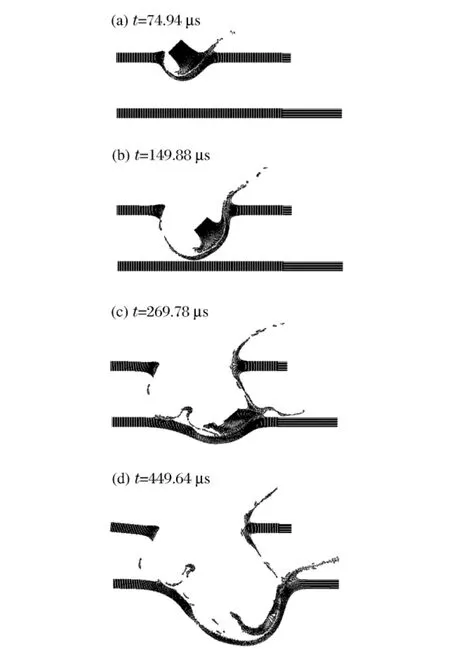
图5 橡皮泥斜撞击材料甲后变形Fig.5 Material deformation when plasticine projectile impacting onto thin X1 target at v=266.9 m/s

为了进一步检验不同材料碰撞下的碰撞相似律准则，对钨弹斜穿透薄钢板进行计算，计算模型如下:钨弹弹体直径1.0 cm，长度2.0 cm，以30°击中钢质靶板，直径和长度分别采用32个粒子和64个粒子离散。靶板1长9.5 cm，厚0.5 cm，靶板2长12.0 cm，厚0.5 cm。总粒子数13 248个。粒子间距Δx为312.5 μm，光滑长度h都为 1.5Δx。钨弹和钢板碰撞速度为 2.0 km/s，碰撞角度 45°，时间步长 10 ns。按照相似律计算橡皮泥与材料甲对应模拟速度为266.9 m/s，时间步长74.94 ns。材料其他参数见表1。

图4～5是两种模型以对应速度斜碰撞后计算结果比较。由图中可以看出:弹体撞击前靶板后迅速将靶板击穿，在靶板上形成一个弹孔。穿透中弹体出现蘑菇头变形，然后与靶板被击穿部分一起破碎，形成碎片云朝板后扩散，扩散角度与入射角基本一致。板前则有部分弹体和靶板破碎粒子以一定角度朝外喷射。碎片云前端集中了绝大部分的破碎粒子，在穿透第一层靶板后撞击第二层靶板，造成后靶板往外激烈拉升变形。可以发现，两种计算模型碰撞后对应时间内弹体的变形基本一致，靶板上弹孔尺寸以及碎片云头部运动距离随时间的变化也一致。但是二者在靶板前端碎片粒子喷射角度则不完全一致，主要原因是在公式（2）推导中，忽略了剪切效应和弹性效应，但二者之间剪切模量和屈服强度的比值不相等，所以计算结果中会出现不一致性。

图6是钨弹30°斜穿透双层薄钢板及橡皮泥斜穿透材料甲双层薄板过程中总能量Ut、动能Uk和内能Ui随时间的变化图。碰撞过程中，动能不断降低并转化为内能，在碰撞达到稳定时动能和内能基本趋向于稳定，由于使用了人工热量控制数值振荡，因此总能量略有变化。但是通过比较也可以看出，在对应的时间里，曲线变化基本一致，即碰撞后的动态响应过程和结果一致。

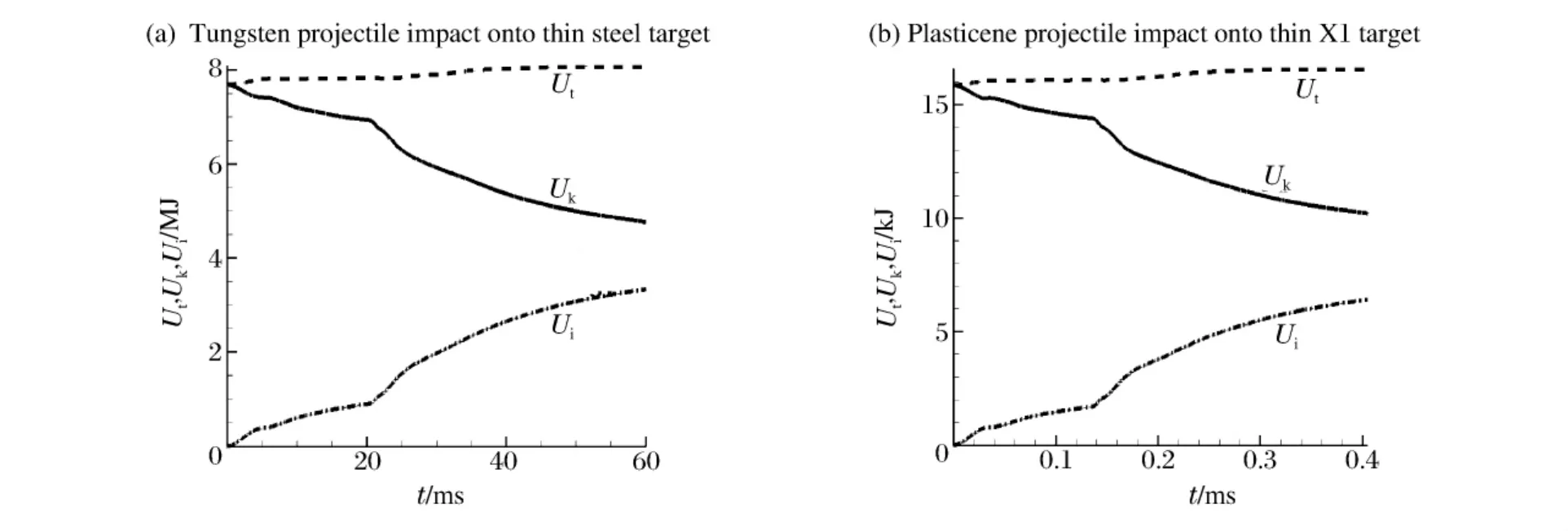
图6 碰撞过程中能量随时间变化Fig.6 Evolution of energy transformation with time

3 结论

通过量纲分析方法对超高速碰撞相似律进行了理论推导，提出了适合于超高速碰撞模拟的相似律准则，然后使用改进的光滑粒子流体动力学方法对厚板开坑、薄板穿透的相似模型进行了计算。计算表明:在超高速碰撞模拟中，存在着一定的碰撞相似准则，这个相似准则跟材料的密度、屈服强度和速度有着直接关系。当材料模型符合这个相似准则时，碰撞后在开坑、开孔尺寸等结果中具有相当的准确性，在碰撞后动态响应效果中也体现了较好的一致性。因此，在满足一定条件的情况下，可以使用可塑性较好的非金属材料代替金属材料用于冲击或碰撞后应力、应变的估算及碰撞过程的模拟。

［1］ 张庆明，黄风雷.超高速碰撞动力学引论［M］.北京:科学出版社，2000:100-104;124;186.

［2］ Johnson W，Travis F W.High-speed cratering in wax and plasticine［J］.International Journal of Mechanical Sciences，1968，10:593-604.

［3］ Carrel J，Johnson W，Travis F W.High-speed impact of plasticine projectiles with laminated plasticine targets［J］.International Journal of Mechanical Sciences，1968，10:677-680.

［4］ 马晓青，韩峰.高速碰撞动力学［M］.北京:国防工业出版社，1998:313-318.

［5］ 马晓青，周兰庭，隋树元.用橡皮泥模拟高速碰撞的实验研究［J］.兵工学报，1989，2:50-54.

MA Xiao-qing，ZHOU Lan-ting，SUI Shu-yuan.Simulating experimental research of high speed impact with plasticine［J］.Acta Armamentarii，1989，2:50-54.

［6］ 谈庆明.量纲分析［M］.合肥:中国科学技术大学出版社，2005:97-98;130-141.

［7］ 谈庆明.高速冲击模型律［C］//王礼立.冲击动力学进展.合肥:中国科学技术大学出版社，1992:303-320.