基于电压调制的永磁容错电机转矩控制系统仿真

沈天珉，胡育文，郝振洋，黄文新

(南京航空航天大学，江苏南京210016)

0 引 言

近年来，多电飞机以及电动汽车得到大力发展，这对飞机电力作动器和电动汽车驱动系统提出了更高的要求，即要具有高的安全可靠性和容错性［1－3］。

永磁容错电机除了具有一般永磁电机体积小、功率密度大和转矩脉动小的特点之外，还具有很强的故障隔离和容错特性。它可以实现相与相之间的电气隔离、磁隔离、物理隔离和热隔离功能，同时保证每相绕组具有较大的电感值，可以抑制短路电流，保证短路相不会对其他正常相工作造成影响［5］。

本文对永磁容错电机和转矩控制算法原理进行了分析，基于永磁容错电机和该控制算法，利用电压调制来实现对转矩的控制，并对其进行了建模和仿真验证。

1 永磁容错电机及其数学模型

永磁容错电机在电机结构上进行了特殊的设计，从而具备故障隔离和抑制短路电流的特性。一台六相十极容错电机模型如图1所示，每相绕组采用集中式绕组隔齿绕制，定子齿采取极靴结构，可以保证各相间的物理隔离、磁隔离、热隔离，同时每相采用单独的H桥驱动，可保证电气隔离。通过电机设计，使绕组的电感接近单位标幺值，可有效抑制短路电流［5］。

永磁容错电机的各相绕组之间互感值近似为零，无磁路耦合。在推导数学模型之前做如下假设:

(1)磁路不饱和，磁滞和涡流损耗忽略不计;

(2)空间磁势及磁通成正弦规律分布;

(3)转子上没有阻尼绕组，永磁体没有阻尼作用;

(4)各相绕组空间对称，每相的电阻、电感值相等。以六相永磁容错电机为例，可得到电压方程:

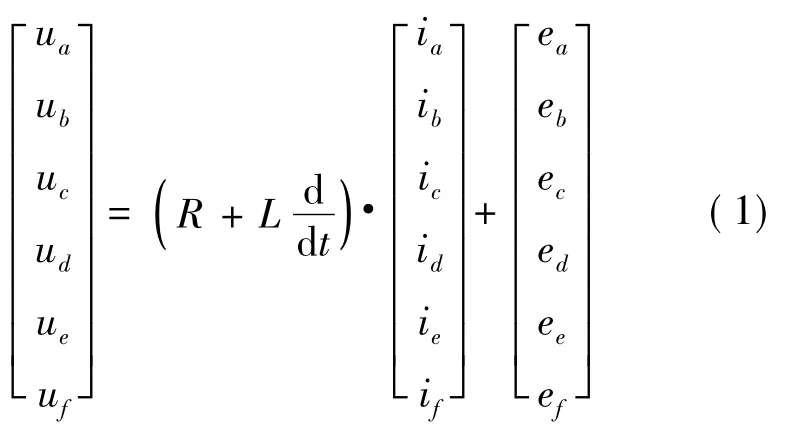
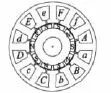
图1 六相十极永磁容错电机结构图

式中:R为相电阻;L为相绕组电感;ua、ub、uc、ud、ue、uf为六相绕组定子端电压;ea、eb、ec、ed、ee、ef为六相绕组反电势;ia、ib、ic、id、ie、if为六相绕组定子电流。

假设磁链在电角度为零时，A相绕组匝链永磁体磁链最大，则六相十极永磁容错电机的反电势方程:

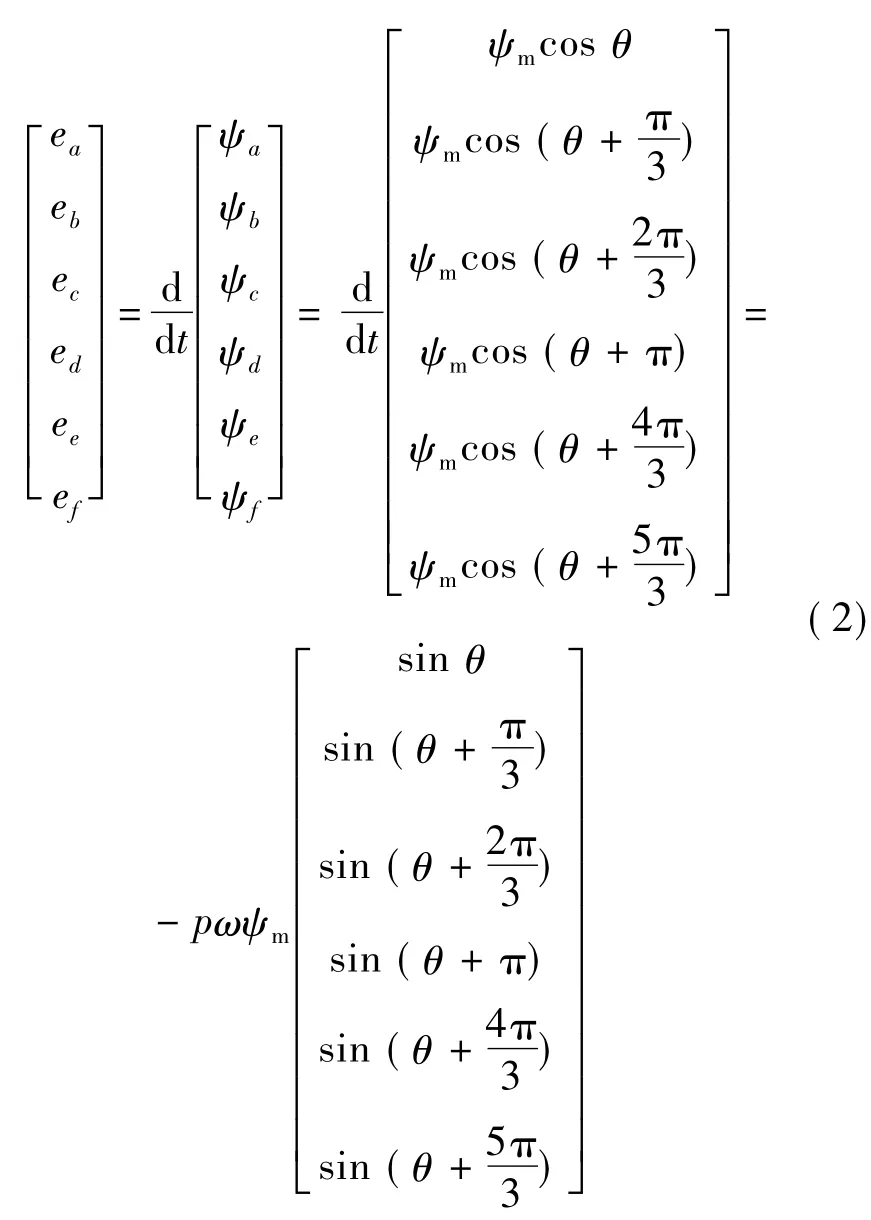
式中: ψa、ψb、ψc、ψd、ψe、ψf为六相绕组反电势磁链;ψm为永磁体磁链幅值;θ为电角度;p为转子极对数。

由功率平衡方程，得到电磁转矩Te:

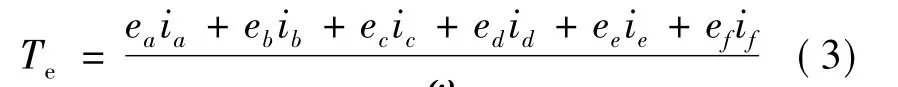
式中:ω为机械角速度。

运动方程:

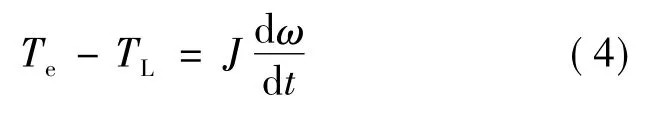
式中:TL为负载转矩;J为电机转动惯量。

2 基于电压调制的转矩控制策略

图2给出了基于电压调制的永磁容错电机转矩控制系统框图。外环为转速环，通过速度调节器得到转矩给定值Td，并将给定值Td送到转矩控制器，转矩控制器接收位置信号以及故障信号，通过转矩算法计算出各相需要的定子磁链给定值，然后通过电压调制，使各相的定子磁链跟踪给定磁链，实现系统的可靠以及一相故障容错运行。转矩控制算法分为正常和故障两种情况。

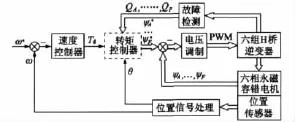
图2 基于电压调制的永磁容错电机转矩控制系统

2.1 各相正常时

最优转矩控制算法的目标是使输出转矩恒定，且定子铜损最小［4］:

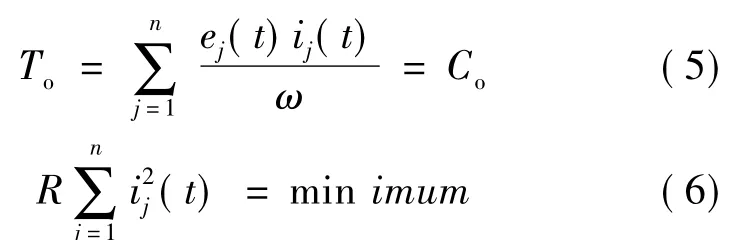
式中:ω为机械角速度;ej(t)为第j相瞬态反电势(j=1，2，…，n);ij(t)为第j相瞬态电流;To为电机电磁转矩;Co为常数。

根据以上两个条件，引入拉格朗日乘数λ，定义价值函数Y为:

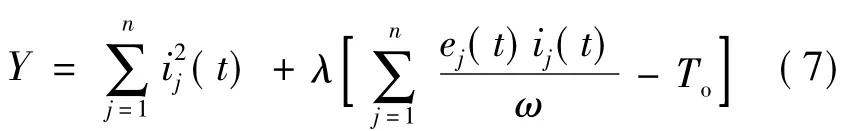
Y满足以下条件:

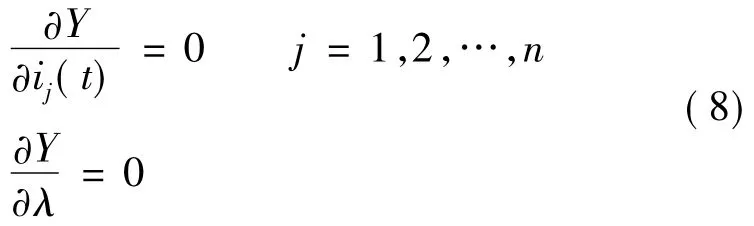
求得各相电流表达式:

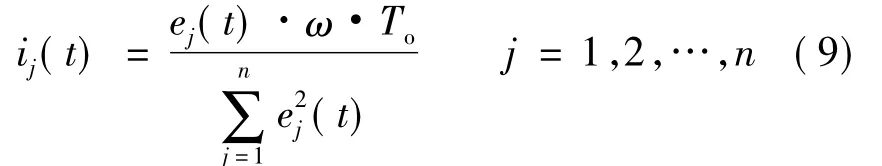
此时各相正常，电流表达式的分母为定值，各相电流为相位互差的正弦波。

在求得每相绕组给定电流后，根据式(10)可以求得每相定子绕组磁链:

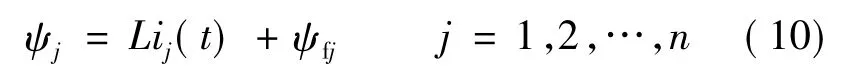
式中:ψj为交链到第j相绕组的定子磁链;ψfj为磁钢磁链交链到第j相定子绕组中磁链;L为相绕组电感。

2.2一相绕组故障时

故障态的最优转矩控制算法与正常态时相似，但需加入故障处理，其控制目标:

式中:Tf(t)为故障相k产生的瞬态转矩。当第k相断路时:

当第k相短路时:

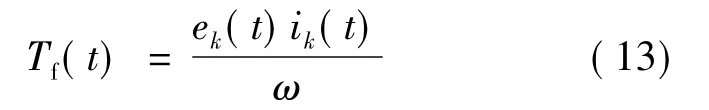
同样取定子铜损最小为约束条件:

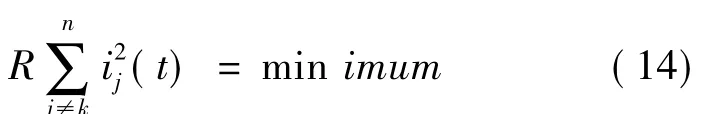
根据以上两个条件，引入拉格朗日乘数λ，定义价值函数Y为:

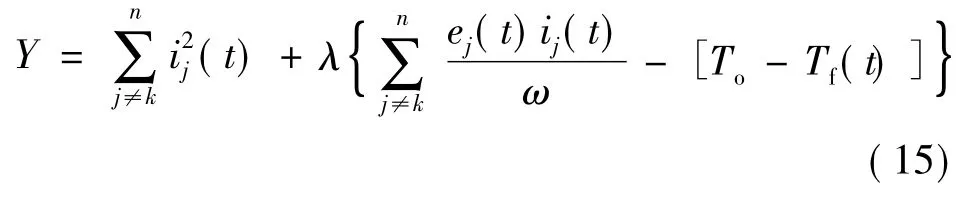
当铜损取最小值时，Y满足以下条件

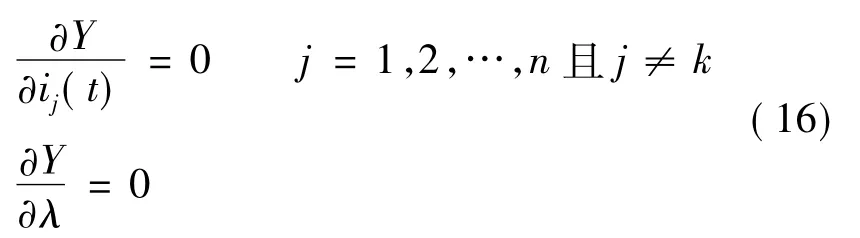
求得各相电流表达式

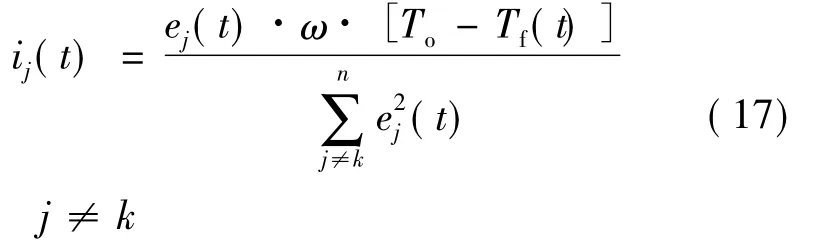
由式(17)可知，电机一相绕组故障时，最优转矩控制算法表达式分母是电角度的函数，由此计算出的正常相电流呈现非正弦。由于该永磁容错电机是按照反电势为正弦来设计，所以式(17)的分母项不会出现极值情况，不需要反复迭代求取最优电流。同样的，根据式(10)可以求出每相定子绕组的磁链，如此，则可以通过电压调制算法，实现对定子磁链的控制。由机电能量转换原理可知，通过对定子磁链的控制，可以实现对电机转矩的控制。

3 电压调制

每个控制周期中，预先计算出定子磁链需要的增量，如下式:

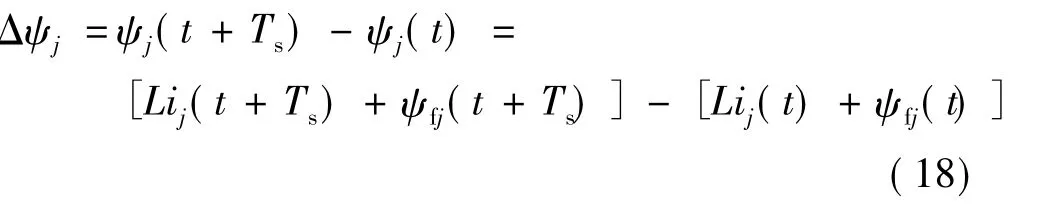
式中:Ts为控制周期。

在一个控制周期内，控制周期很短，可以认为转子位置基本不变，即ψfj(t+Ts)≈ψfj(t)，因此可将式(18)简化为式(19)，有:

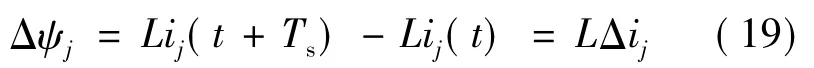
永磁容错电机的每相绕组电压方程可写为下式:

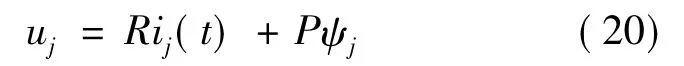
如果忽略定子电阻，则有:

将式(21)改写为式(22)，如下式:

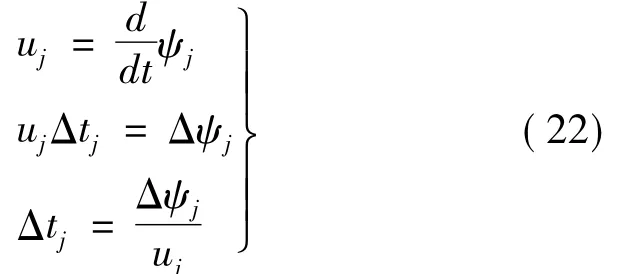
由式(19)得到磁链增量，然后通过式(22)计算出一个周期内需要施加的电压的理论时间。在式(22)中，Δtj表示一个控制周期内第j相定子绕组上理论需要施加电压的时间，但由于控制系统为数字控制系统，一个控制周期内只能够改变一次PWM状态，所以要考虑在一个PWM周期内，绕组两端施加电压反向后的影响，因此，上面计算出的时间不是最终施加电压的时间，应该作如下处理:

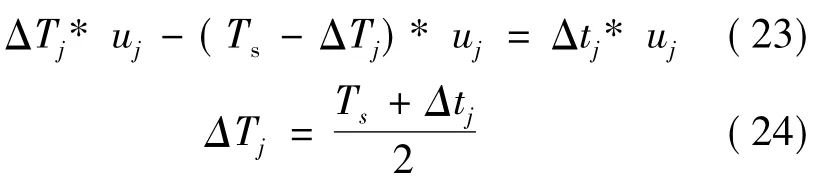
ΔTj表示一个控制周期内第j相定子绕组上实际需要施加电压的时间，如果计算出的时间ΔTj大于控制周期Ts，则取控制时间为控制周期Ts的值，即 ΔTj=Ts。

4 仿真验证

为了验证系统的可行性，在Matlab/Simulink环境中建立仿真模型，以验证六相正常分别切换到一相短路和一相断路两种情况，为了便于比较，短路和断路故障均采用A相。整个控制系统包括故障诊断、转矩控制算法、电压调制算法和转速PI调节器四个部分。

仿真参数设置如下:负载转矩TL=1 N·m;给定转速n*=2 000 r/min;直流母线电压Udc=270 V;断路发生时刻0.02 s;短路发生时刻0.02 s;控制周期为62.5 μs。

图3 A相断路情况下的波形

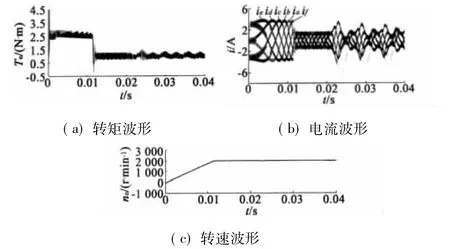
图4 A相短路情况下的波形

图3给出了A相断路故障前后的仿真波形，在0.02 s时A相发生断路故障，可以看出，在发生A相断路故障前，六相电流为依次互差60°电角度的正弦波，当发生故障后，电流变为不规则波形，且发生故障后，某些正常相电流会变大，以补偿平均转矩和抵消转矩脉动。整个过程中，转矩平均值较正常情况时不变，转矩脉动在正常态为28%，断路后为28.2%，转矩脉动在故障前后基本不变。转速在故障前后也都能够稳定在给定值 。图4给出了A相短路故障前后的仿真波形，控制周期为62.5μs，在0.02 s时A相发生短路故障。故障前，各相电流均为正弦波，当A相出现短路故障后，某些正常相电流会变大，以补偿平均转矩和抵消脉动转矩，转速在故障前后都能够稳定在给定值。转矩脉动在正常态为28%，短路后为30%，转矩脉动在故障前后变化不大。短路相电流的直流分量呈指数衰减至零，稳定后短路相电流为周期性变化的正弦波，且只比额定值稍大，为额定值的1.2倍，这是由于永磁容错电机的电感标幺化设计具有抑制短路电流的能力［5］。

5 结 语

本文对永磁容错电机和转矩控制算法进行了分析，提出基于电压调制的转矩控制方法，建立了与实际情况基本一致的仿真模型。仿真结果验证了算法的正确性，能够实现一相短路或断路容错运行，且转矩、转速性能与正常态相比基本不变。

［1]Anthony S.The development of a highly reliable power management and distribution system for transport air－craft［J］.AIAA，1994，12(8):1－6.

［2]Joseph A，Weimer A.Power technology for the more electrical aircraft［R］.Aerospace design conference，AIAA，93:16－19.

［3]郝振洋，胡育文，黄文新.电力作动器中永磁容错电机及其控制系统的发展［J］.航空学报，2008，29(1):65－74.

［4]Edu J D，Atallah K，Wang J B，et al.Modular Fault Tolerant Permanent Magnet Brushless Machines［J］.IEE Proceedings of Power Electronics，Machines and Drives，2002，487:415－420.

［5]郝振洋，胡育文，黄文新，等.电力作动器中永磁容错电机的电感和谐波分析［J］.航空学报，2009，30(6):1063－1069.