开关磁阻发电机输出电压控制

刘 香，易灵芝，陈海燕，王方方

(湘潭大学，湖南湘潭411105)

0 引 言

开关磁阻发电机(以下简称SRG)结构简单，调节、控制灵活，转子侧无磁源、无绕组，有很强的容错能力，适合高温、高速、振动等恶劣环境，近年来得到广泛的研究与关注。但是由于SRG的双凸极结构，使得内部的电磁关系复杂，SRG的非线性，使其控制技术十分困难。为了控制SRG的直流电压，在文献［1］中提出PI控制方法，但是SRG是在外部原动机的驱动下工作的，在不同的驱动转矩下，采用常规固定参数的PI控制需要不停地对参数进行整定，控制较复杂，并且无法对SRG进行实时控制。在文献［2］中提出逆机模型，在文献［3］中提到公差带控制的方法，但是这些方法都要基于被控对象的精确数学模型。

近年来模糊控制已经运用到电机驱动系统，如感应伺服驱动系统［3］，甚至开关磁阻电机调速系统中。本文将模糊控制方法应用到SRG的输出电压上，通过理论分析和实际仿真证明了模糊控制方法在非线性SRG系统控制电压是可行的。其静动态响应比常规的PID控制算法效果更好。甚至在驱动转矩变化，PID控制无法进行实时仿真时，模糊控制体现了方便、迅速等优越性。

1 SRG电压控制理论分析

1.1 SR电机发电条件

图1 一相电流波形图

SR电机只有定子上有绕组，励磁绕组和电枢绕组合二为一。因此其发电本质与一般的发电机不同，以一相导通为例，θon～θoff阶段，电源对绕组进行供电，称为励磁阶段，励磁开始，与此同时励磁电流开始上升。当转子转到θ=θm时，相电流iphase＞0。当转子转到时，SR电机进入发电区域，在本阶段，SR电机开始吸收机械能，为了对电机进行充分励磁，提高发电能力，需要将关断角θoff适当后移。当θ≥θoff时，主开关管关断，绕组内能量沿续流二极管回馈给蓄电池，电机进入续流发电状态，续流电流不断地将机械能转换成能量输出。SR电机进入发电状态基本电路方程:

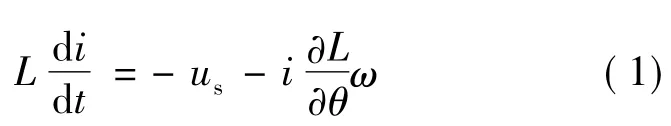
1.2 SRG电压控制原理

SRG在原动机的驱动下产生电流，电流经过储能元件生成电压。电流之间的关系如图2所示。

由电路的基本定律可知:

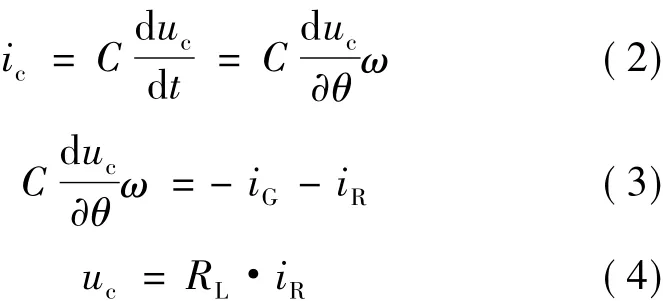
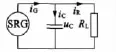
图2 SR电机发电过程中电流流向

解这个一阶线性方程得:

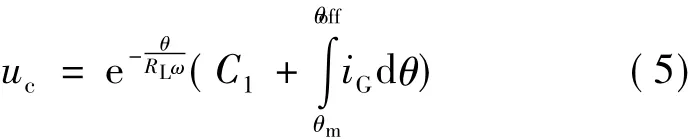
式中:C1为积分常量;θ为导通角。

SRG作恒压源时输出必须并联电容，但是由于绕组给电容周期性的充放电，因此电容的电压是脉动的。由式(5)可知，uc是受θ、ω系数的影响，所以可以通过控制θ和ω达到调节uc的目的。

1.3 SRG电压控制系统简介

图3是模糊逻辑控制的一个SRG闭环系统，其中把SRG可以看作为一个黑箱，直流电压Ud为输出开关角θon和θoff作为输入，输出和输入的关系:

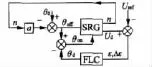
图3 模糊控制SRG电压系统

将SRG的输出转速n作为一个反馈到输入端，构成一个转速外环的闭环控制:

其中:θ0为设定值;a为常数;

将实时输出电压Ud和参考电压Uref的差值ε，和差值ε的变化率Δε作为FLC的输入，导通角θd作为FLC的输出，SRG的输入信号θon可以确定为:

2 模糊逻辑控制器

在实际应用中，模糊控制器先离线完成模糊控制表的设计，然后再进行在线查表控制。模糊控制基于专家经验总结出若干条模糊控制规则，用来描述具有不确定性、复杂对象的模糊关系，通过被控系统输出的差值及差值变化率得到模糊关系的推理合成获得控制量，从而对系统进行控制。

2.1 确定模糊控制的输入和输出量

将参考电压Uref和实时输出电压的Ud差值ε，和差值ε的变化率Δε作为FLC的输入，导通角θd作为FLC的输出(如图3所示)将每个采样时刻电机的电压差值ε(nT)、差值变化量Δε(nT)模糊化，从而得到模糊集，分别为:

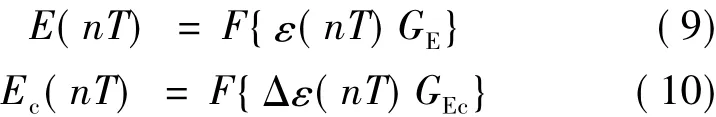
式中:GE、GEc分别为电压差值和差值变化的量化因子;T为采样周期。

2.2 隶属函数与控制规则的确定

取 ε、Δε 和 θd的论域均为［－6，6］，将模糊子集都分为7档{负大，负中，负小，零，正小，正中，正大}，可表示为{NB，NM，NS，ZE，PS，PM，PB}。ε、Δε和θd的模糊子集的隶属度函数的形状都选择为三角型，如图4所示。

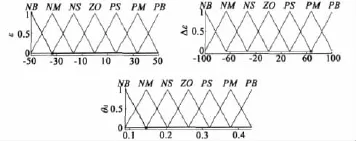
图4 隶属度函数均匀分布图

模糊规则制定的合理与否直接影响着SRG系统的性能。根据上述理论分析导通角和电压的关系，当电压误差ε为负时，实际电压小于给定电压，电压下降，要求电压上升，应该增大导通角θd;同理当电压误差为正时，实际电压高于给定电压，电压上升，要求电压下降，应该减小导通角θd。综合考虑两个输入量的影响，并根据专家经验得到以下49条模糊控制规则。

如表1所示。

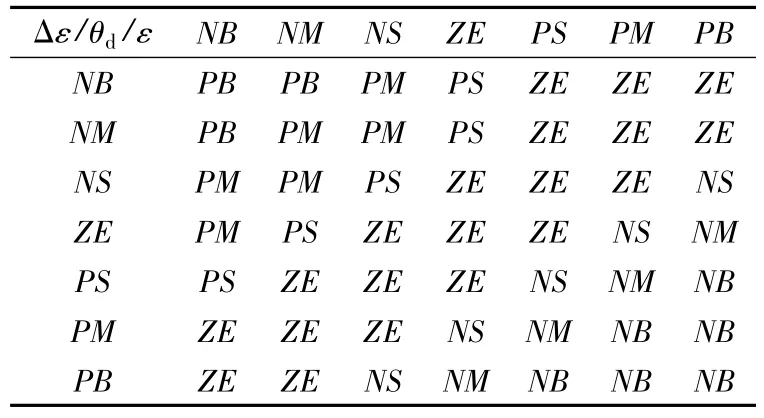
表1 模糊规则表

2.3 模糊量化因子的确定

虽然取 ε、Δε 和 θd的论域均为［－6，6］，构成只含有{－6，－5，－4，－3，－2，－1，0，1，2，3，4，5，6}，13个离散集合，但实际系统的精确变化范围不可能只在［－6，6］之间，如果其基本论域在［m，n］之间，则可以通过变换:

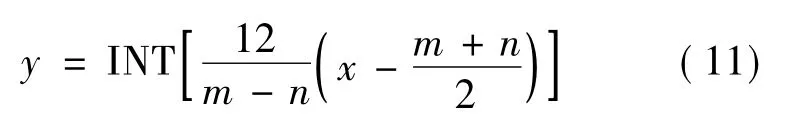
将在［m，n］间变化的变量x转化为［－6，6］间变化的变量y。例如:电机电压差值在［－50 V，50 V］间变化，则偏差对应的量化因子GE=12/100，若实测偏差x=20 V，则按式(11)计算取整得y=2;设电压差值变化范围［－100 V，100 V］，则差值变化对应的量化因子GEC=12/200，若实际偏差变化x=20 V时，则y=1.2，取整为1。模糊规则建立之后，设计模糊控制器的下一步将是进行模糊推理。模糊推理的算法很多，本文采用 CRI的 Mandani推理方法。反模糊的方法很多，本文应用的是重心法。表2显示了采用重心法实现了模糊判决求得的精确量的控制表。

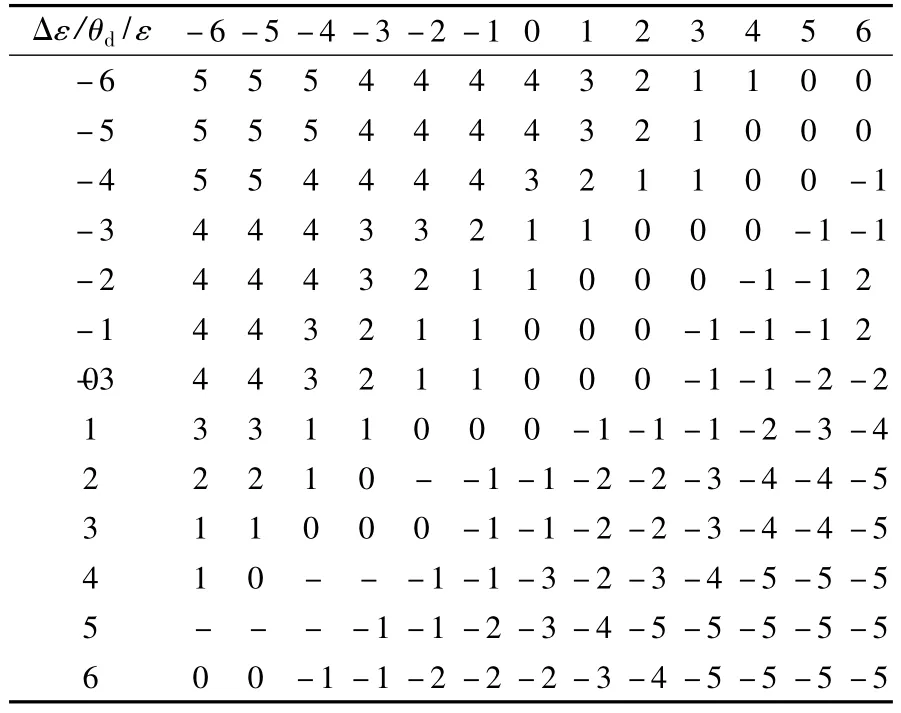
表2 模糊规则控制表

3 仿真并结果分析

用基于模糊控制SRG的输出电压，对四相(8/6)SR电机进行仿真，额定功率为750 W，绕组电阻R=0.15 Ω，Lmax=0.11 H，Lmin=0.01 H，仿真参数:针对自励式发电模式，励磁电容C=2 500μF，励磁电感L=650 mH，负载Rm=300Ω，转动惯量J=0.001 5 kg·m2，摩擦系数F=0.018 3。

基于Simulink建立的仿真模型如图5所示。

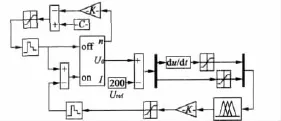
图5 整体仿真模型

图6是电压偏差、电压偏差变化和导通角(conduct angle)模糊规则曲面关系。

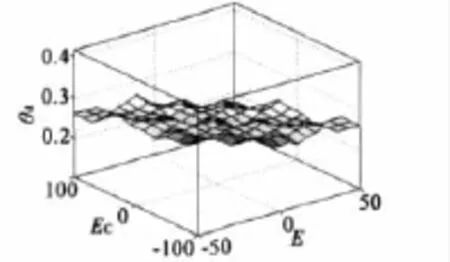
图6 模糊规则曲面关系图

图7给定参考电压U=200 V、驱动转矩T=2.5 N·m时，采用传统PID控制与模糊控制时候转速和电压仿真结果。可以看出，恒定的转矩产生恒定的电压，模糊控制比传统的PI控制的超调量小，整个动态响应提高，电压波纹小，而且模糊控制转速波动比传统PID控制小。

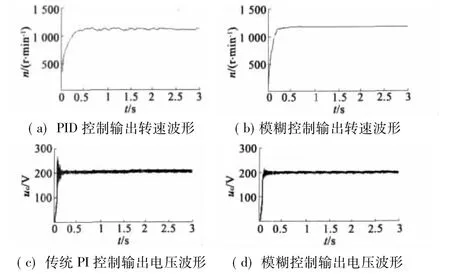
图7 恒定转矩时的仿真波形

图8给定参考电压U=200 V，t=1 s时驱动转矩T由2.5 N·m升高为3 N·m，t=2 s时驱动转矩由3 N·m降为2 N·m采用模糊控制时的转速和输出电压波形。传统的PI控制需要在这两个转矩变化阶段不断地整定参数，无法实现实时控制，所以无法得到相应的电压波形，而此时模糊控制控制充分体现了实时控制的优势。

图8 转矩变化时输出的电压波形

4 结 语

本文采用模糊控制方法来控制SRG输出电压结果表明:模糊控制运用在SRG上，提高了系统动态特性，减小静态误差。并与传统的PI控制进行比较，采用模糊控制的系统能及时适应内部参数变化、提高系统的鲁棒性，减小稳态误差。充分体现了应用模糊控制有不可比拟的优越性。

［1]Stiebler M，Gotovac S.A Switched Reluctance Servo Drive［C］//In:Proceeding of the EPE＇93.Bringhton UK，1993:436－441.

［2]Kjaer PC，Cossar C，Gribble JJ，et al.Switched Reluctance Generator ControlUsing an Inverse Machine Model［C］//Proceedings of the ICEM＇94.Paris，France，1994:380－385.

［3]Liu K，Stiebler M.Sinzulatiori of the Peifortizatice of a Switched Reluctance Generator［C］//Proceeding of the 40.IWK.Ilmenau，Germany，1995.

［4]Liu K，Stiebler M.Voltage control of a switched reluctance generator by means of fuzzy logic approach［J］.Proceedings of the 6th International Conference on Optimization of Electrical and Electronic Equipments，1998:443－446.

［5]刘北阳，张奕黄，杨岳峰.模糊PI控制在开关磁阻发电机中的应用［J］.微特电机，2009(4):54－56.

［6]钟坤炎.开关磁阻发电系统建模与控制研究［D］.湘潭大学，2009.