基于逆系统的双馈变速恒频发电机组的控制研究

张继勇，张苏新，卞皓玮

(扬州大学，江苏扬州225009)

0 引 言

风能是比较廉价和有很好发展前景的一种新能源。现在世界很多国家都很重视对于风能的开发利用，在风力发电领域变速恒频发电系统已是一种主流，尤其对于双馈感应电机的利用尤为突出。

由于风力发电机是强耦合，多变量的非线性机电系统，经典控制难以满足系统的控制精度及动态性能要求。目前多采用基于矢量控制系统的策略，网侧采用了电网电压定向矢量控制［3－4］，机侧则采用了定子磁场定向。但仍存在一些问题:(1)对扰动及其参数变化较敏感;(2)对直流母线电压的恒定和单位功率因数控制的稳定性并不是很好。

逆系统方法是一种非线性系统反馈线性化控制的新理论，该方法物理概念清晰，适用面广，应用简便，已成功应用于一些系统控制。文献［5，7］针对矢量控制存在的一些问题，提出了一种逆系统方法，为分析和设计风力发电网侧变换器控制提供了便利。本文采用基于逆系统方法来控制双馈风力发电系统，并进行了计算机仿真。仿真结果表明该控制系统具有较好的稳定性能和动态性能。

1 DFIG及网侧变换器模型

1.1 DFIG风力发电系统结构

DFIG发电系统基本结构如图1所示。

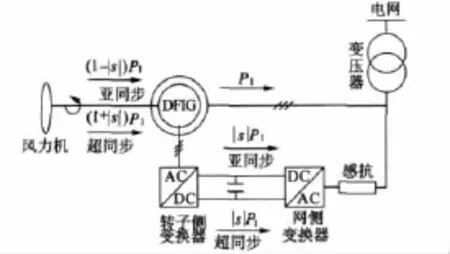
图1 DFIG风力发电基本结构图

对于风力发电的双馈电机来说，主要运行于亚同步和超同步速状态，功率流向如图1所示。系统包含双PWM变换器，即网侧和转子侧变换器。

1.2 双馈风力发电网侧变换器数学模型

变速恒频风力发电系统要求网侧变换器控制直流母线电压稳定，保持单位功率因数，并且实现有功和无功功率的解耦。为了实现三相PWM变换器的高性能控制，首先需要建立并分析它的数学模型，通过坐标变换转化为dq坐标系下的数学表达式。图2为三相PWM变换器网侧拓扑结构图。

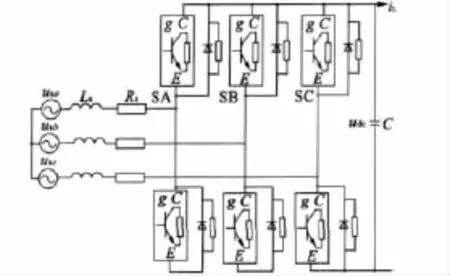
图2 网侧变流器结构

根据图2，在abc坐标系下的数学模型，再根据坐标变换原理，实现abc到dq坐标变换，可得三相电压型PWM变换器在dq坐标系下的数学模型:

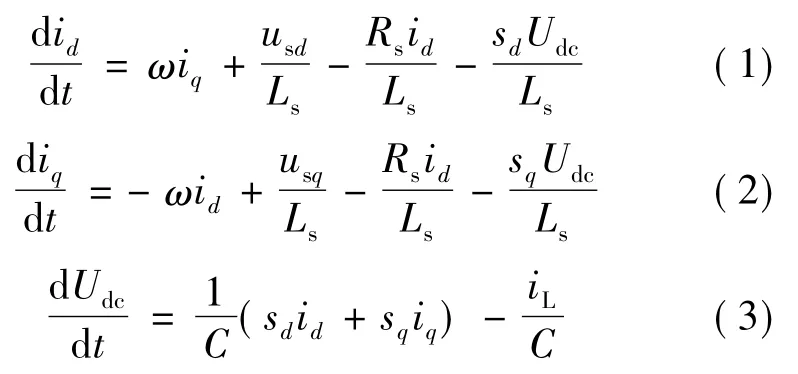
在dq坐标系下，输入的复功率为:

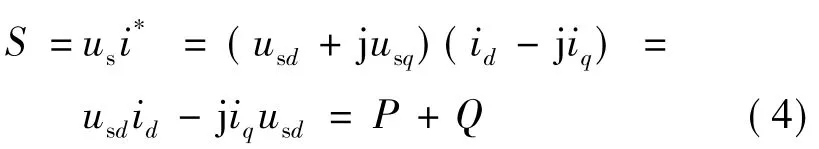
由式(5)可知，网侧变换器的有功功率和无功功率分别由id和iq控制:

2 DFIG网侧变换器逆系统控制结构

所谓逆系统控制方法就是通过构造可实现的α阶逆系统将原系统补偿成为具有线性传递关系的且已解耦的伪线性复合系统，然后对已线性化的系统或线性化解耦的各子系统设计闭环控制器，形成复合控制器(复合控制系统)的控制方法，如图3所示。

根据上述推导可选取系统状态变量:

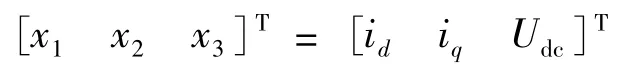
选取输出变量:

图3 由α阶逆系统与闭环控制器构成的复合控制器

选取输入变量:

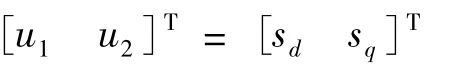
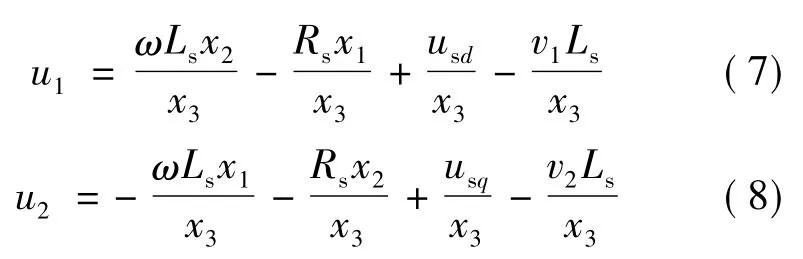
三相网侧PWM变换器控制系统的目标是:使系统电流电压同相位，即单位功率因数，且直流母线电压恒定，根据上述条件，系统在稳态时，可以令:

代入式(1)～式(3)并化简:

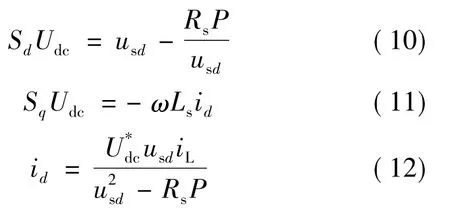
当Rs较小时可将其忽略，则id的稳态值:

为了消除系统滤波电阻Rs的影响，消除直流电，:压稳态误差 将 修改

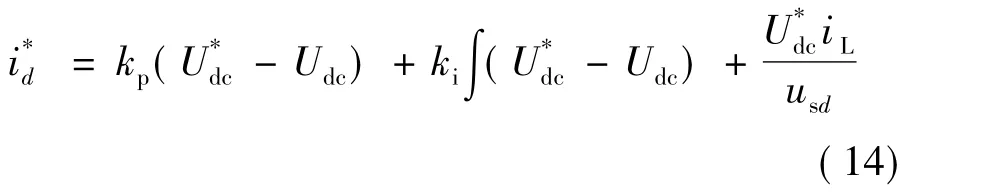
闭环控制器可以通过传递函数来求取。设传递函数:

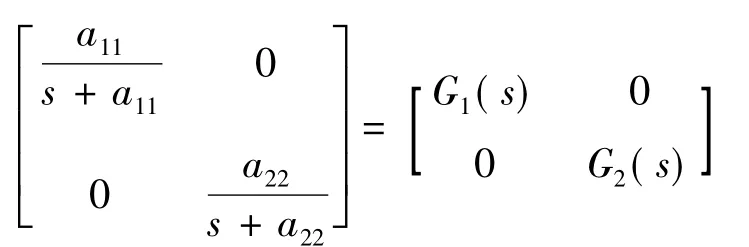
为了实现其传递函数，变换控制系统的表达式:

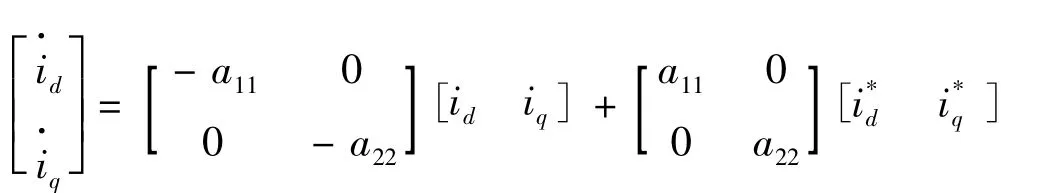
上式表明系统的输出可以通过传递函数G(s)追踪系统的输入。如果输入取参考值，那么期望的电流输出就能取得。系统控制结构图如图4所示。

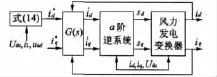
图4 系统控制框图

3 控制系统的结构

本文设计的基于逆系统的结构如图5所示。

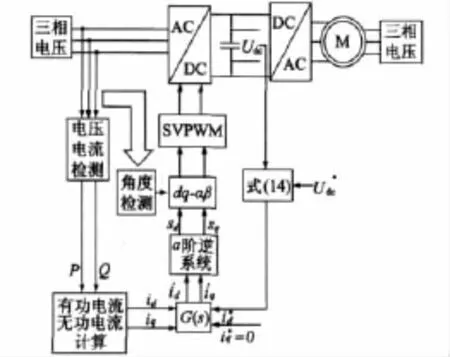
图5 基于逆系统控制方法的系统结构图

用电压、电流传感器测得的数值进行运算，得到有功无功功率。图中变换的角度可以通过角度检测器检测。SVPWM模块为电压空间矢量模块，控制变流器六个桥的导通或关断。该模块的使用使变流桥开关频率恒定，便于交流侧滤波电感的设计。

4 仿真验证

为了验证本文提出的伪线性逆系统控制方案的正确性，本文使用Matlab/Simulink软件对控制系统进行了仿真。仿真参数为:双馈电机额定功率2.5 kW，定子电阻0.435Ω，转子漏感2 mH，转子电阻0.816 Ω，转子漏感 69.31 mH，转动惯量 0.089 kg/m2;网侧交流电压有效值75 V，直流母线电压140 V，进线电阻Rs=0.05Ω，进线电感Ls=6 mH，直流母线电容C=2 200μF。

当DFIG稳定运行时，定子侧向电网输出的有功功率一定，根据最大功率捕捉和功率平衡，当风力机输入功率发生变化时，变换器功率也发生变化。如果风速减小使转差率变为原来的两倍，则变换器向风机提供的有功功率|S|P1增大到原来的两倍。

图6a为直流母线电压图。在0.2 s前，发电机处于稳定状态时，直流母线电压稳定。0.2 s后风速减小有功功率增加，母线电压有所波动。但过段时间后电压又保持恒定，实现了直流母线电压的稳定。

图6b为相电压相电流的仿真图，电压与电流同相位，实现了交流侧单位功率因数，在0.2 s时有功功率增加一倍，相电流近似为原来的两倍。

图6c～图6f分别为无功功率、有功功率、功率因数和相电流频谱的仿真图，从图中可以看出，实现了无功和有功的解耦，无功功率在有功功率变化时依然等于零，且能维持单位功率因数，且谐波分量非常小。仿真结果可以看出该控制方法具有较好的动态稳定性。

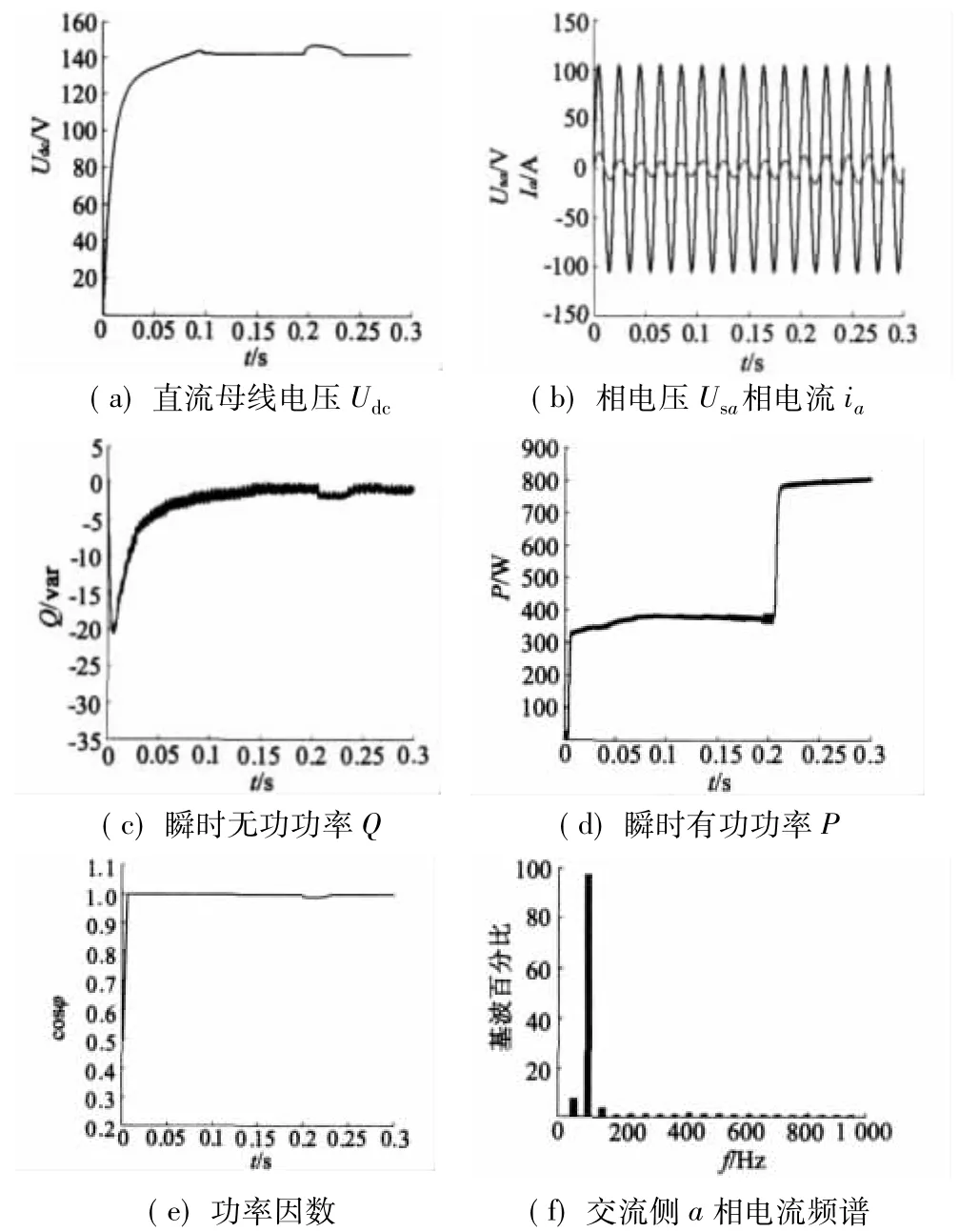
图6 转子输入电能有功功率增加，逆系统仿真波形

图7a、图7b分别为A相电压在0.25 s跌落10%时，A相电压及电流和直流母线电压的仿真图，并且相电压在0.3 s恢复。从图中可以看出，电压跌落时，相电流增加，但依然能保持同相位，而直流母线电压有所波动，一段时间后直流母线电压仍能稳定。仿真结果表明该控制方法具有较好的动态稳定性。

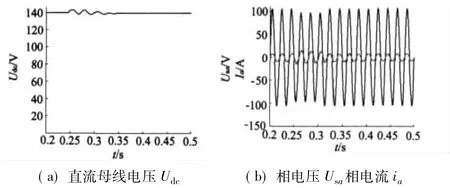
图7 A相电压在0.25 s跌落10%时逆系统仿真模型

5 结 语

本文在变速恒频风力发电网侧变换器数学模型的基础上，通过逆系统理论及控制模型，构造了伪线性控制系统，通过dq电流的解耦控制，实现了有功无功功率的解耦，利用闭环控制器控制提高了系统的稳定性，通过Matlab/Simulink仿真对所提出的控制方法进行了验证，仿真结果表明本文所提出的伪线性逆系统控制策略具有较好的动态性和稳定性。

［1]李春文，冯元坤.多变量非线性控制的逆系统［M］.北京:清华大学出版社，1991.

［2]王兆安，黄俊.电力电子技术［M］.北京:机械工业出版社，2000.

［3]林渭勋.现代电力电子技术［M］.北京:机械工业出版社，2007.

［4]陈伯时.电力拖动自动控制系统－运动控制系统(第3版)［M］.北京:机械工业出版社，2003.

［5]戴先中，刘国海，张兴华.交流传动神经网络逆控制［M］.北京:机械工业出版社，2007.

［6]张崇魏，张兴.PWM整流器及其控制［M］.北京:机械工业出版社，2003.

［7]李泰，王奔.基于逆系统方法的三相PWM整流器直接功率控制［J］.电气传动，2008，38(10):33－38.

［8]Trzynadlowski A M，Legowaki S F.Minimum－loss Vector PWM Strategy for Three－phase Inverters［J］.IEEE Trans.Power Electron，1994，9(2):26－34.

［9]Jie F，Huang J.Novel Modulation Method for Direct Power Control of Three－phase PWM Rectifier［J］.Power Electronics，2006，40(4):9－11.

［10]Sira Ramire H.Nolinear P－I controller design for switchmode DC－to－DC power converters［J］.IEEE Trans.Circuit Syst.，1991，38(4):410－417.

［11]Pena R，Clare JC，Asher GM.Doubly fed induction generation using back－to－back PWM converters and its application to variable speed wind energy generation［J］.IEEE Proceedings－Electric Power Applications，1996，143(3):231－241.

［12]Rioual P，Poliquen H，Louis J P.Non－linear control of PWM rectifier by feedback linearization and exact PWM control［C］//Conf.Rec.IEEE PESC＇94，1994:1095－1102.

［13]Leithead W E，Salle SD，Reardon D.Role and objictives of control for wind turbines［J］.IEEE Proc.Part.C，1991:135－148.

［14]Chedid R.Intelligent Control for Wind Energy Conversion Systems［J］.Wind Engineering，1998，22(1):1－16.

［15]Ackermann T，Soder L.An overview of wind energy－status 2002［J］.Renewable and Sustainable Energy Reviews，2002，6(1－2):67－127.

［16]Lee T S.Nolinear state feedback control design for three－phase PWM boost rectifiers using extended linearization［J］.IEEE Proc.Power Appl.，2003:546－554.