基于矢量控制的永磁同步电动机回馈制动的仿真与研究

全 力，张德望，朱孝勇，顾剑波

(江苏大学，江苏镇江212013)

0 引 言

近年来，电动汽车作为零污染的新能源汽车受到世界各国的高度重视，而再生制动作为提高电动汽车电能利用率的重要手段，已成为研究热点之一。同时，永磁同步电动机以体积小、重量轻、效率高的优点在电动汽车中正在获得广泛应用，本文根据电动汽车再生制动的特点，从永磁同步电动机的模型出发，分析了在不同定子电流矢量下的电机感应电势和转矩，以及直流侧电压对电机转矩的影响，论述了在整个回馈制动过程中如何实现定子电流的矢量控制，最后确定了永磁同步电动机回馈制动的优化方案，给出仿真结果。

1 永磁同步电动机矢量控制系统简介

矢量控制的基本原理是通过测量和控制电机定子电流矢量，根据磁场定向原理分别对电机的励磁电流和转矩电流进行控制，从而达到控制异步电动机转矩的目的。对永磁同步电动机来说，转子磁通是由转子上的永磁体激励产生的，故通过检测电机的转子位置就可知电机的转子磁通，因此PMSM矢量控制的实质就是控制定子电流空间矢量相位和幅值。在磁场定向坐标上，将电流矢量分解成两个相互垂直、彼此独立的矢量id(励磁分量)和iq(转矩分量)。永磁体的励磁磁链和交直轴电流确定后，电机的转矩只取决于定子电流矢量id和iq，控制id和iq即可控制电机的转矩。通过电流调节环，使实际id和iq跟踪指令id和iq，以实现对电机转矩和转速的控制。

本文将矢量控制原理引入到回馈制动中，以实现永磁同步电动机在回馈制动过程中制动转矩的可控。图1是PMSM基于矢量控制的回馈制动的原理框图，电机的回馈制动工况与电动工况不同，对速度没有固定的要求，所以没有速度闭环控制。而回馈制动主要是转矩的要求，以得到一个恒定的减速度。

在回馈制动工况下，定、转子磁链矢量夹角为负，即转子磁链矢量超前定子磁链矢量。首先根据制动强度的要求，计算电机的制动转矩，由此得到iq，并设定适当的id(在本文中id=0)。经坐标转换计算出三相绕组的给定电流和电压矢量幅值u。然后，采用电流滞环控制策略控制三相制动电流ia、ib、ic，并根据电压矢量幅值u的大小适当地调节直流侧电压UDC。

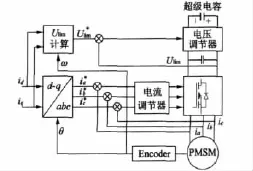
图1 PMSM矢量控制的回馈制动功能框图

2 电流滞环控制策略研究

本文所提到的电流滞环控制不同于传统的方式，不仅要实现三相电流呈正弦变化，更主要的是实现制动电流回馈到直流侧，为了实现这两点，本文另辟蹊径，重新设计了开关管的开关方式。在本文中，电流滞环控制是调节其中两相的相电流，而非三相，因ia+ib+ic=0，故调节其中两相电流可以实现第三相电流的间接控制。

在本文中按三相电流变化划分为6种状态，在每种状态下都是采用控制其中两相电流而进一步控制第三相电流的方式，具体方法是选择电流方向相同的两相电流为直接控制对象。例如电机的电流从A、B两相流入，C相流出，则选取ia、ib为直接控制对象，ic为间接控制对象。

如图2所示，当ia、ib小于给定值i*a、i*b时，导通 VT1、VT3、VT6，其余关断。制动电流ia、ib在电源电压和电机感应电势的共同作用下逐渐增大，此时ia的流向是电源正极→VT1→A→C→VT6→电源负极，ib的流向是电源正极→VT3→B→C→VT6→电源负极，这个阶段电机处于反接制动。

随着电流ia、ib不断增大，当某一相电流大于给定值，假如ib＞i*b时，关断VT3，此时ib的流向是B→C→VT6→VT4→B，这个阶段电机的部分绕组处于反接制动状态，部分绕组处于能耗制动。

当ia、ib大于给定值i*a、i*b，关断所有的 MOS管，因6个MOS管内部寄生的二极管，此时相电流ia、ib流入电源正极，从电源负极流出，因为电源电压高于电机感应电势，所以在电源电压的作用下，ia、ib逐渐减小。这个阶段电机处于回馈制动。

总之，整个过程是在反接制动、能耗制动和回馈制动之间相互来回切换，切换的目的是实现对电流的滞环控制。而在切换过程中电源也处于回收电能和释放电能的转换中，但总体上，电源是在回收电能。

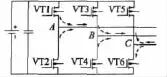
图2 主电路拓扑图

3 直流侧电压的控制策略研究

永磁同步电动机的电压方程:

由此可得:

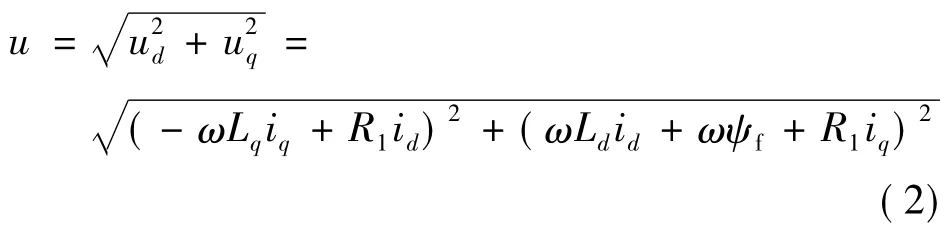
一般地，电机主要工作在转速较高的工况下，由于此时电机的电抗要远大于电阻，所以忽略电阻上的压降不计，则上式可以简化:

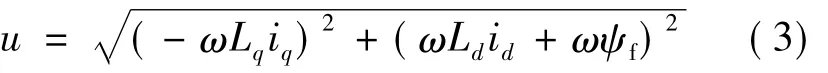
由式(3)可知，电机绕组上的电压降大小主要取决于两个因素:电机的运行转速和电机的定子电流矢量。在一般情况下，逆变器直流侧电压大小是固定的，由于直流侧电压限制了相电压有效值的极限值Ulim，因而直流侧电压会进一步制约电机的运行转速和定子电流矢量。简单地说，在电机高速运行时，由于逆变器直流侧电压的限制作用，很难获得一个幅值较大的定子电流矢量，所以在电机高速运行时，电机可以输出的最大转矩小。假设逆变器直流侧电压为UDC，电机采用Y型接法，则最大基波相电压有效值:

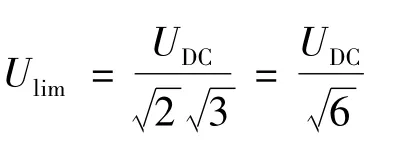
在dq轴系统中的电压极限值为以ulim代替上式中的u，有:

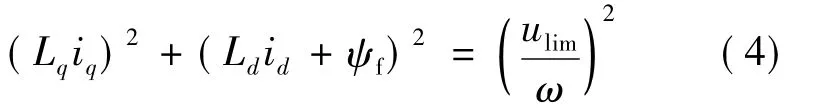
本文所提到的电机为隐极式永磁同步电动机，在隐极式永磁同步电动机中，Ld=Lq，当电机运行在某一个给定转速时，式(4)是一个以圆心半径为的圆方程，再将式(4)表示在图3的i、i dq平面上，即可得到在此转速下电机运行的电压极限轨迹－电压极限圆。在该转速下，电机稳态运行，定子电流矢量只能落在该转速的电压极限圆内，最多只能落在极限圆上，绝不能超过圆轨迹。而电压极限圆的半径与转速成反比，因此随着电机转速的不断提高，电压极限圆不断缩小，从而形成了一组圆曲线。

图3 隐极式电机的电压极限圆

从图3可知，随着电机转速不断上升，电机的定子电流矢量的极限值也愈来愈小。而电机的磁链与电流矢量的关系:

则电机转矩方程:

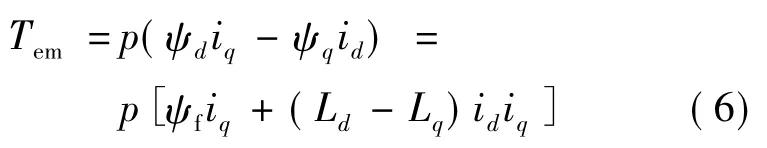
在隐极式永磁同步电动机中，Ld=Lq，可得:

所以，随着转速的不断上升，电机可输出的最大转矩也会不断地下降。当电机运行在高速时，在直流侧电压不变的情况下，电机可输出转矩已经很小了。

电机的输入功率:

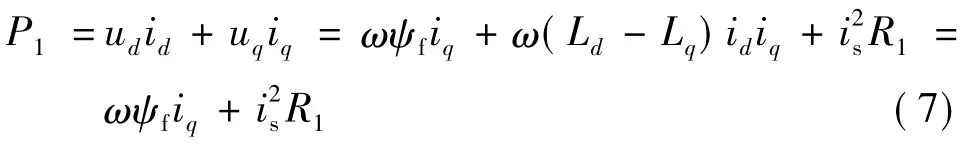
电磁功率:

在恒转矩的前提下，为了达到电机效率最大，涉及到最小的定子电流矢量的问题，定子电流越小，电机的损耗就越小，效率越高，所需的逆变器容量也越低。对于隐极式电机来说，最大效率控制即id=0控制，此时iq=is。由此可得:

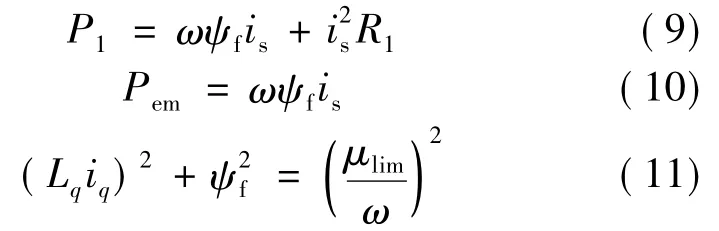
当电机处于电动状态时，高速运行工况对电机的输出转矩要求并不高，因此逆变器直流侧电压固定可以满足需求;而在电机制动状态下，在电机高转速时，为了实现电机迅速停转，通常伴随着高转矩的要求，因此在制动时，为了解决高转速高转矩不能兼顾的问题，本文提出了提高逆变器直流侧电压UDC的方案。

图4 直流侧电压控制示意图

在图4中，超级电容是电机回馈制动的储能容器，采用电压滞环方式控制直流侧电压UDC。首先，根据电机转速和制动电流求出电压极限值ulim，进而计算出直流侧电压接着，通过MOS管的通断控制直流侧电压UDC。MOS管关断时，在电机的回馈电流作用下，直流侧电压逐渐增大;MOS管开通时，直流侧的电能通过MOS管转移到超级电容中，此时直流侧电压逐渐下降。这样，通过比较UDC和U*DC，确定MOS管的通断，从而实现对直流侧电压UDC的滞环控制。

在电压滞环控制方式下，直流侧的电容相当于一个临时储能容器，直接吸收电机的回馈电能，而超级电容作为最终的储能容器，回收的电能最终储存在超级电容中。

4 Simulink仿真结果分析

为了提高效率，本文采用计算机仿真软件Matlab，并利用其仿真工具Simulink提供的功能进行建模仿真与分析。

为了避免电流矢量落在电压极限圆内，在制动过程中，直流侧电压是变化的，在制动转矩恒定时，电压值大小与转速成正比，故而直流侧电压呈直线下降，直至与额定电压持平(额定电压取决于电源电压)，如图5所示。

图6是直流侧电流曲线，因为电机的发电功率约等于回收功率:ΩTem≈UDCIDC，又因为电机转矩恒定，转速直线下降，所以在直流侧电压直线下降期间，直流侧电流几乎维持恒定，当直流侧电压达到额定电压时，电流绝对值直线下降。

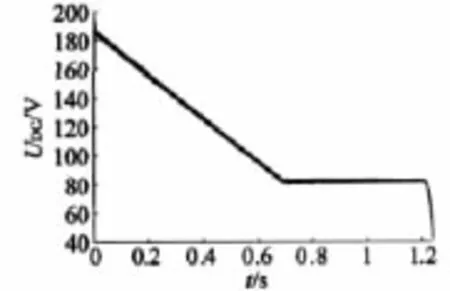
图5 直流侧电压

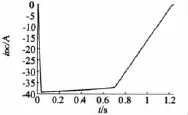
图6 直流侧电流

图7表明电机处于匀减速制动工况下，图8中的电机输出转矩为负且为恒定值，这表明电机输出一个恒定的制动转矩。

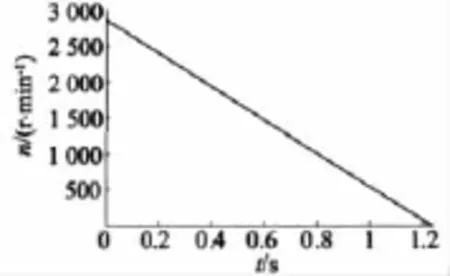
图7 电机转速仿真曲线

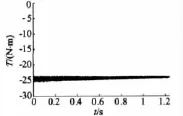
图8 电机输出转矩仿真曲线

5 结 论

通过对Matlab/Simulink仿真结果的理论分析和研究，可以得到以下结论:

(1)在整个回馈制动的过程中，电机的制动转矩恒定且可控，实现了电机的匀减速制动;

(2)在回馈制动时，电机可以运行在高转速高转矩的工况下，突破了电动时电机不能同时高转速高转矩运行的限制;

(3)本文设计的电流滞环控制策略和电压滞环控制策略均可以在仿真环境下实现。各种电流波形和电压波形均与理论分析一致。电机的动能得到有效的回收。

［1]陈伯时.电力拖动自动控制系统［M］.北京:机械工业出版社，2006.

［2]徐祖华，黄智伟，盛义发.永磁同步电机直接转矩控制理论基础与仿真研究［J］.微特电机，2003(5):6－8.

［3]纪志成，周寰，李三东.基于PSIM永磁同步电机矢量控制系统的仿真建模［J］.系统仿真学报，2004(5):898－901.

［4]陈荣，邓智泉，严仰光.基于转子磁场定向控制的永磁同步电机制动过程分析［J］.电工技术学报，2004(9):30－36.

［5]赵云，李叶松.永磁同步电机宽范围最大转矩控制［J］.电工技术学报，2010(7):45－50.

［6]何亚屏，年晓红.永磁同步电机矢量控制MATLAB仿真研究［J］.变流技术与电力牵引，2007(6):58－62.