双馈感应风电机组建模控制仿真

张 帆，李国庆，张宇阳，张万林

(1.东北电力大学 电气工程学院，吉林吉林132012;2.吉林市供电公司，吉林 吉林132011)

随着风力发电技术的发展，双馈风电机组逐步成为兆瓦级风力发电机组的主力机型，双馈风电机组与传统定速风电机组相比有显著的优越性:通过调节发电机转子电流的大小、频率和相位，从而实现转速的调节;可在很宽的风速范围内保持最佳叶尖速比，进而实现风能最大转换效率;可以采用一定的控制策略灵活调节系统的有功、无功功率，减少损耗，提高系统效率［1，2］。励磁技术和桨距调节技术的结合，构成了变速恒频风力发电控制系统。结构与性能的特性对DFIG风机的控制提出了更高的要求，性能优良的控制策略是提高风能利用效率及电能质量的可靠保证［3］。文献［4］采用气隙磁场定向的控制策略，实现了定子端口有功和无功的解耦，然而在实际系统中准确定向气隙磁场并不容易，这增加了控制系统的复杂性。文献［5］采用直接功率控制，研究结果表明系统具有很好的鲁棒性，然而由于采用滞环比较器，导致励磁控制器的调节对发电机及其系统的冲击较大。本文采用定子磁链定向的控制策略，结合应用在风力机部份的桨距角限速控制策略，实现了DFIG发电机变速恒频运行、有功功率、无功功率的解耦控制以及原动机最优效率跟踪运行等基本性能，且动态性能良好。

1 基于双馈感应发电机的风电机组模型

1.1 空气动力模型

风力发电机的空气动力数学模型为［6］

式中:Pmec为风力机从风中抽取的机械功率;ρ为空气密度;R为风力机桨叶半径;v为风速;λ为叶尖速比;β为桨距角;Cp为风能转换系数，是λ和β的函数。

1.2 轴系模型

文献［7］指出，只有采用风力机与发电机两质块模型，才能满足在电网故障情况下对风机暂态过程的精确描述。其数学模型为:

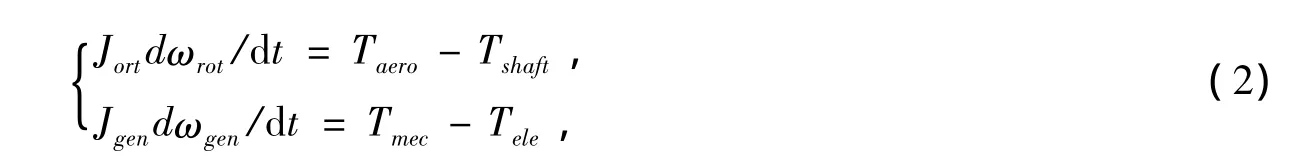
其中，Jrot，Jgen为风力机，发电机转动惯量，ωrot，ωgen为风力机，发电机转子转速，Taero，Tshaft，Tmec，Tele为空气动力转矩，轴系转矩，机械转矩和电磁转矩。其中，Tshaft，Tmec满足Tshaft/Tmec=ngear，ngear，为变速比。在稳态时，Taero=Tshaft，Tmec=Tele，而在暂态时，该模型将表现出类似弹簧一样的扭矩特性。

1.3 DFIG电机及转子侧变流器模型

在DFIG风电机组中，转子侧变流器输出的电压即为发电机的转子励磁电压，因此将DFIG电机及转子侧变流器一起建模。文献［8］给出了感应电动机在三相坐标系中的模型，经过坐标变换转换成同步旋转的dq0坐标系下的模型，其中同步角速度取为电网频率ω1，定向方式采用定子磁链定向。

其磁链方程为:

功率方程为:

(3)～(5)式中，ωs为坐标系旋转角速度，即同步转速;v、i、ψ为绕组的电压、电流及磁链;R为绕组电阻;P、Q代表有功和无功;Ls、Lr为定子绕阻与转子绕组的自感;Lm为定、转子绕组互感;下标s、r代表电机的定子与转子;下标d、q分别代表电机d、q的绕组;s为转差率。

1.4 网侧变流器模型

网侧变流器的运行状态与Statcom类似，文献［9］给出了VSC变流器在三相坐标系中的模型，经过坐标变换转换成同步旋转的dq0坐标系下的模型，其中同步角速度取为电网频率ω1，定向方式采用电网电压。

功率方程为:

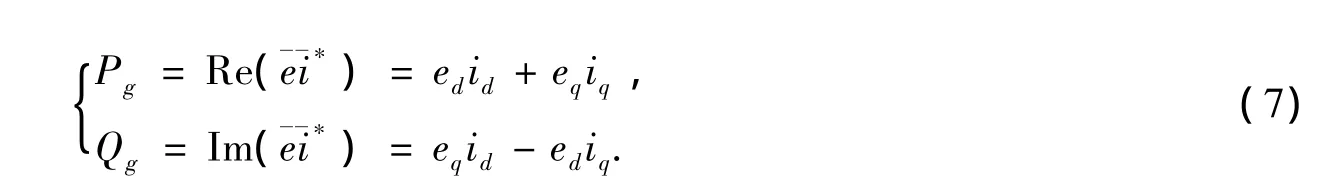
(6)～(7)式中:C为直流侧电容值;Udc电容电压值;L、R为电容与电网之间的连接电感及等值电阻;Ud、Uq为电网电压d、q的分量;ed、eq为变流器d、q输出的有效值。

2 双馈感应发电机联网控制策略

2.1 风力机动力部份控制策略

风力机动力部份控制的核心是对DFIG风机的桨距角进行控制。桨距角限速控制的原理简单，效果良好且容易实现。其中心思想是把发电机转速作为桨距角控制的唯一指标。当发电机转速因为风速过大或电网发生故障而上升时，控制桨距角增大以减小风机从风中捕获的电能，当发电机转速没有越限时，控制桨距角恒为零度，以最大程度获取风能。桨距角控制框图如图1所示。其调节功能是通过PI控制器实现的，为了使控制系统更接近真实情况，计及了伺服系统的时间常数Tservo以及桨距角变化率限制，并设计了一个计划增益表格以补偿Cp(λ，β)中关于β的非线性特性［10］。

2.2 DFIG转子侧变流器控制策略

DFIG的交流励磁调速控制是通过转子侧变流器产生合适的变频电源来实现的。当采用定子磁链定向(ψsd= ψs，ψsq=0)，并忽略定子电阻，结合式(4)、(5)可导出:

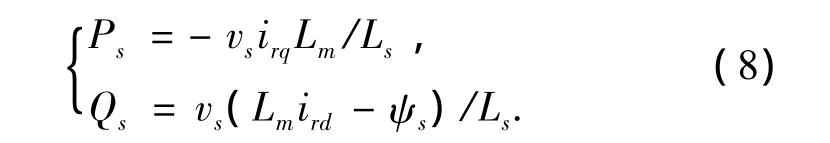
图1 桨距角控制框图

由上式可知，转子电流的有功电流分量irq可以控制定子输出的有功功率Ps，而无功电流分量ird可以控制定子输出的无功功率Qs，它们之间不存在耦合关系。实现了对定子绕组有功功率Ps与无功功率Qs的解耦控制。由于控制系统的控制作用最终都是通过作用在变流器上的电压相量来实现的，所以必须建立转子电流相量与转子电压相量之间的关系。

由式(3)、(4)、(8)可导出:

从式(9)可以看出，虽然在采用定子磁场定向时，转子有功电流分量与无功电流分量是解耦的，但是转子电压控制分量却不完全解耦，如果用vrd控制ird，viq控制irq，则需要分别加入前馈补偿△vrd，△vrq，这样才能实现对功率的解耦控制［11］。△vrd，△vrq分别为:

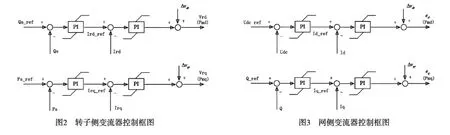
转子侧变流器的控制框图如图2所示。其中Ps_ref按照风力机的最大风能捕获功率计算给出，Qs_ref根据双馈感应发电机不同的无功功率控制策略计算给出:当要求双馈感应风力发电机按恒功率因数控制时，控制机组的无功功率，使机组按规定的功率因数运行;当要求机组按恒电压控制时，则根据系统的无功功率要求，调节机组的无功功率，可使机端电压稳定在设定值。

2.3 DFIG网侧变流器控制策略

网侧变流器的控制策略与转子侧变流器相似，不同的是采用了电网电压定向的方式(Ud=U，Uq=0)。在该定向方式下，由式(6)、(7)可导出:

基于式(11)、(12)可以设计出转子侧变流器的控制框图如图3所示。其中Udc_ref为电容电压的给定值，恒为电容器的额定电压，Qref根据不同的无功功率控制策略计算给出，正常情况下恒为零，在故障时可发出适当无功以支持电网电压。

3 模型与控制策略的仿真验证

在DIgSILENT仿真平台应用上文所述的DFIG模型及控制策略。其风机参数为Prate=5MVA，Rs=0.003，Xs=0.125，Rr=0.004，Xr=0.05，Rcr=0.01，Xm=2.5，以上参数未标明单位的皆为标幺值，搭建DFIG模型接入220 KV电网，接入点的短路容量为150 MVA。

3.1 DFIG对调度变化的响应仿真

图4为DFIG在正常运行情况下，分别改变定子有功，定子无功，及网侧变流器参考值时，实际值随参考值的响应变化，从图中可知，无论是有功减少还是无功的增加，DFIG风机都能迅速响应调度的要求，并且过渡过程比较平稳，这充分体现了DFIG风机可控性强这一优点，充分利用这一优点可以有效地增加电网的稳定性。其中网侧变流器无功功率变化速度快且几乎没有暂态过程，这是因为定子有功无功的变化伴随着机电暂态过程，而网侧变流器无功功率的变化通过电力电子器件即可完成，这也体现了柔性交流输电的优点。

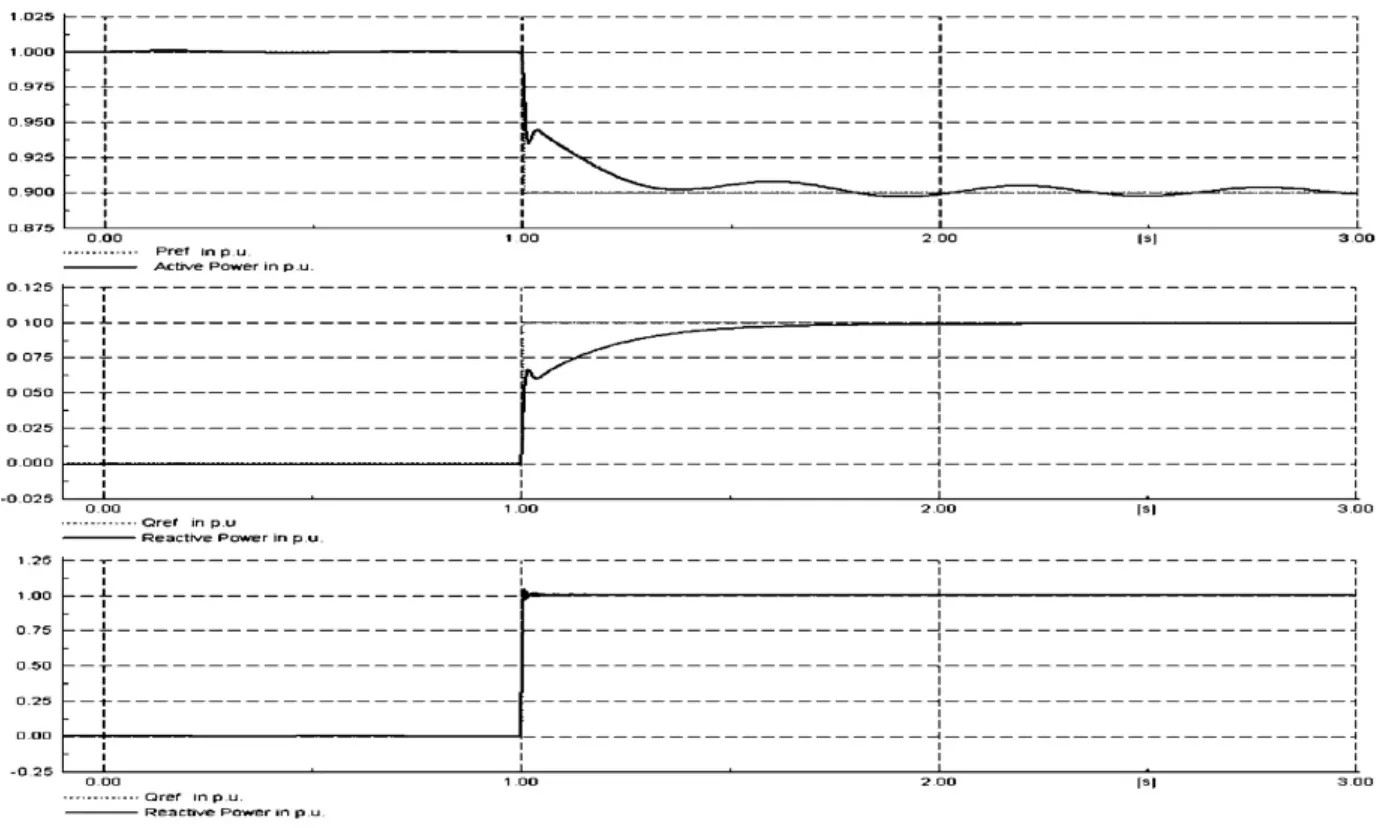
图4 DFIG对调度变化的响应仿真

3.2 DFIG对阶越风速变化的响应仿真

图5为DFIG在每5 s增加1 m/s的风速下发电机转子转速，桨距角以及有功功率变化的仿真。由仿真结果可以看出，随着风速的不断增加，发电机的转速以及定子发出的有功功率均在不断地上升。当发电机转速达到1.1pu时，定子有功功率变为1pu后，在此运行点风速再上升时，桨距角开始逐渐升高，以减少风力机从风中汲取的能量，发电机转速以及定子有功功率不再继续上升而保持相对平稳。而桨距角为变化的速度由快到慢则体现了风轮机本身的非线性特性，这一点已在桨距角限速策略中予以考虑。由此看出，DFIG风机可在很宽的风速范围内发电，发电机转子转速也可在较宽范围(s=-0.1～0.3)内运行，这充分体现出变速恒频风机的优点。

图5 DFIG对阶越风速变化的响应仿真

图6 DFIG低电压穿越能力仿真

3.3 DFIG低电压穿越能力仿真

随着风机装机容量在电网中所占比例越来越高，各国电网公司都要求并网风机具有低电压穿越能力(LVRT，low voltage ride through)。即在风机并网点电压跌落的时候，风机能够保持并网，甚至向电网提供一定的无功功率，支持电网恢复，直到电网恢复正常，从而“穿越”这个低电压时间。在严重故障下，DFIG风机的转子侧变流器容易因转子过电流损坏。所以普遍使用Crowbar电路为转子过电流提供旁路以保护变流器，以便在恰当的时刻重新投入运行。

为研究所建风机的LVRT能力，0 s时在风电场出口通制短路制造电压跌落为85%的电压降，0.3 s时故障消失，图6分别为转子电流、定子有功以及定子无功的暂态过程。观察知，在故障发生瞬间，转子电流迅速增大，触发了Crow2bar保护，DFIG电机作为普通感应电机运行，0.3 s故障消失后一到两个周波Crowbar保护退出运行，转子电流出现二次峰值，这容易再次触动Crowbar电路的投入。定子有功与无功在震荡中逐渐恢复到故障前的状态。仿真结果表明采用桨距角限速控制及基于定子磁链定向的矢量控制的DFIG风机具备了一定的低电压穿越能力。

4 结 论

(1)建立了DFIG风机的9阶数学模型，该模型在暂态仿真中具有足够精度。在风力机动力部分采用桨距角限速控制策略，在发电机电气部分采应用定子磁链定向的矢量控制策略。

(2)DFIG风力发电机可通过转子侧变流器改变励磁控制发电机定子有功与无功功率，通过网侧变流器维持直流母线电压并向电网发出一定的无功。

(3)DFIG可以在较宽的风速范围内运行，可工作在超同步速与次同步速两种状态，具有良好的可控性，且在各种工况下保持较高效率。

(4)采用该控制策略的DFIG风机具备一定的低电压穿越能力，但转子电流抑制效果较差。

［1］Mattia Marinelli，Andrea Morini.Modeling of Doubly Fed Induction Generator Equipped Wind Turbine for Dynamic Studies［C］.Universities Power Engineering Conference，UPEC 2008.43rd International:1 -6.

［2］尹明，李庚银，周明，赵成勇.双馈感应风力发电机组动态模型的分析与比较［J］.电力系统自动化，2006，30(13):22-27.

［3］迟永宁，王伟胜，刘燕华.大型风电场对电力系统暂态稳定性的影响［J］.电力系统自动化，2006，30(15):10-14.

［4］Mitsutoshi Yamamoto，Osamu Motoyoshi.Active and Reactive Power Control for Doubly-fed Wound Rotor Induction Generator［J］.IEEE Trans.ON Power Electronics，1991，6(4):62 -64.

［5］张俊峰，毛承雄，陆继明.双陆继明感应发电机的直接功率控制策略［J］.电力系统自动化设备，2006，26(4):31-35.

［6］Prabha.Kundur.Power System Stability and Control［M］.北京:中国电力出版社，2001:458 -461.

［7］迟永宁，王伟胜，戴慧珠.改善基于双馈感应发电机的并网风电场暂态电压稳定性研究［J］.中国电机工程学报，2007，27(25):25-31.

［8］郑太一，严干贵，周志强，穆钢，崔杨，黄亚峰.电网电压跌落时风电机组运行仿真与实证分析［J］.电力系统及其自动化学报，2009，21(3):90-97.

［9］Petru T，Thiringer T.Modeling of wind turbines for Power system studies［J］.IEEE Trans on Power Systems，2002，17(4):1132 - 1139.

［10］Debiprasad Panda，Eric L.A Novel Control Strategy for the Rotor Side Control of a Doubly-fed Induction Machine［C］.IECON 2001，1695 -1702.

［11］李晶，王伟胜.大型变速恒频风力发电机组建模与仿真［J］.中国电机工程学报，2004，24(6):100-105.