直流调制对电力系统小扰动稳定性影响分析

陈厚合，徐 双，李国庆，姜 涛，邓 超

(1.东北电力大学 电气工程学院，吉林 吉林132012;2.随州供电公司，湖北随州441300)

随着“西电东送，南北互供，大区联网”战略实施，我国电网规模不断扩大、输送容量及电压等级不断提高，通过己建成的交直流输电通道，东部地区负荷中心、西南地区水电基地及北方地区火电基地基本实现互联［1-3］。根据规划到2020年左右我国基本实现全国范围内电网互联。大区电网互联使得系统可跨区域补偿、水火互济，有利于电网错峰调度、机组紧急备用、系统故障紧急支援等诸多好处［4-6］。然而，在大区互联电网带来诸多优势的同时，区域间低频振荡已成为限制互联系统输电能力，影响电网安全稳定运行的重要因素之一［7-9］。利用直流系统的功率调制可有效抑制互联电网振荡，改善系统运行稳定性［10-14］。

直流功率调制是指在直流控制系统中加入附加直流功率调制器，从两端交流系统或并联交流联络线上提取反映系统异常的信号来调节直流输电系统传输的有功功率，使之快速补偿或吸收其所联交流系统的功率缺额或过剩，起到阻尼振荡和紧急支援的作用［15］。为全面分析直流功率调制对电力系统动态稳定性影响，本文构建含直流输电系统的多机系统Heffron-Phillips模型，借助模态分析理论分析直流无功率调制和有功率调制对系统小扰动稳定性影响，并应用根轨迹法对直流功率调制控制器进行设计，最后通过算例仿真验证直流功率调制的可行性和调制策略的合理性。

1 HVDC系统模型

常用的换流器直流部分模型如图1所示，其数学模型为:

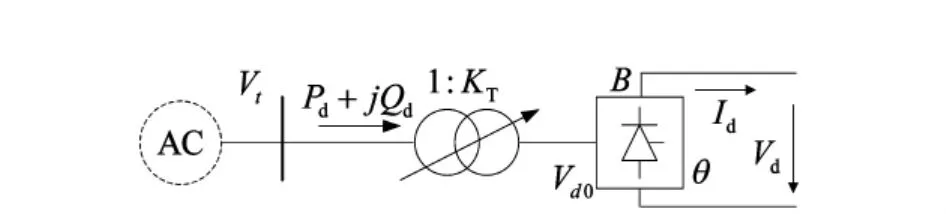
图1 直流系统模型

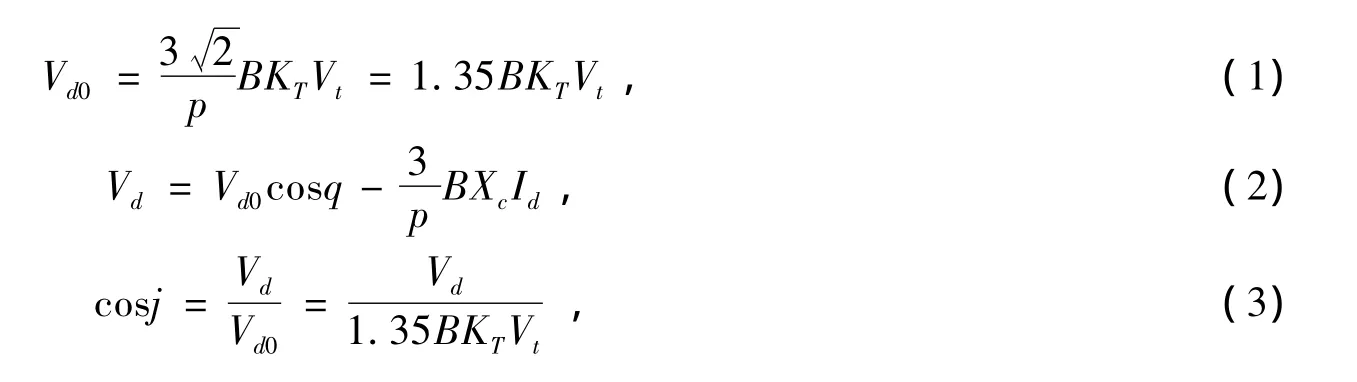
(1)～(5)式中:Vt为换流变压器高压母线电压有效值;KT为换流变压器变比;B为换流器桥数;φ为功率因数角;Pd和Qd分别为换流站吸收的有功和无功功率;Xc为单桥换流电抗;Vd为换流器节点直流侧电压;Vd0为换流器节点直流侧空载电压;Id为换流器节点直流侧电流，流出节点为正;cosθ为整流器触发角α或逆变器熄弧角γ的余弦值。

图2 直流输电系统控制系统示意图

直流输电系统高度可控，通过对换流器的快速调节，控制直流输电线路输送的功率大小和方向，以满足整个交直流混合系统的运行要求，即直流输电系统性能极大程度依赖于控制系统。控制系统应能将直流功率、直流电压、直流电流及换流器触发角等控制量限制在直流输电系统稳态运行极限范围内，还应将直流系统的暂态过电流及暂态过电压限制在设备允许运行的范围内，并保证在交流或直流系统故障后，能在规定的响应时间内恢复到稳态运行状态，直流输电控制系统如图2所示。由图2可知换流器是直流输电控制系统的基础，直流输电系统控制功能都是通过对换流器控制实现对直流输电系统的控制，换流器常用控制方式有:定功率控制(CP)、定电流控制(CC)、定电压控制(CV)和定角度控制(CA)，相应的控制方程为:

(6)～(9)式中:上角标sp表示预设值;定角度控制为整流器定触发角α或逆变器定熄弧角γ。

图3 直流附加控制器框图

根据换流器不同控制方式，结合整个直流输电系统特点，直流输电系统控制策略有:整流侧定功率—逆变侧定熄弧角、整流侧定电流—逆变侧定熄弧角、整流侧定电流—逆变侧定电压、整流侧定电压—逆变侧定电流等。直流输电系统运行过程中，直流输电系统的控制策略对交流系统频率不敏感，利用直流输电系统进行功率调制改善交流系统的动态稳定性时，需在直流控制系统的主控制层加入附加控制器(如图2)，常用的直流附加控制器类似于PSS采用单输入单输出超前—滞后补偿控制，附加控制器控制框图如图3所示，由图3的直流附加控制器可得出直流功率调制系统的传递函数为:

2 Heffron-Phillips模型

20世纪60年代，北美电力系统发生了低频振荡后，F.P.deMello和C.Concordia采用了Heffron-Phillips模型分析电力系统低频振荡发生的原因，利用Heffron-Phillips模型分析电力系统小扰动稳定性时认为，发电机AVR的调节作用将产生电磁力矩，该力矩可分解为同步力矩分量和阻尼力矩分量，与功角变化同向的同步力矩分量是正同步力矩分量，与功角变化反向的同步力矩分量是负同步力矩分量;与转速变化同向的阻尼力矩分量为正阻尼力矩分量，与转速变化反向的阻尼力矩分量为负阻尼力矩分量。当电力系统运行在远距离、重负荷等条件下时，为维持发电机机端电压恒定，AVR增益变大，导致产生的阻尼力矩分量与转速变化反向，因而是负阻尼力矩分量;AVR的负阻尼分量将抵消发电机固有的部分正阻尼分量，当负阻尼分量等于或超过正阻尼分量时，发电机处于弱阻尼或负阻尼状态。系统出现扰动后，发电机会出现低频振荡，由于发电机缺乏足够的正阻尼力矩，将导致发电机持续等幅振荡或增幅振荡，最终破坏系统的稳定性。即AVR的负阻尼作用是产生系统低频振荡的根本原因，从而很好地揭示了电力系统低频振荡产生的物理本质［16-18］。Heffron-Phillips模型框图如图4所示，根据该图得出的线性化模型如下:

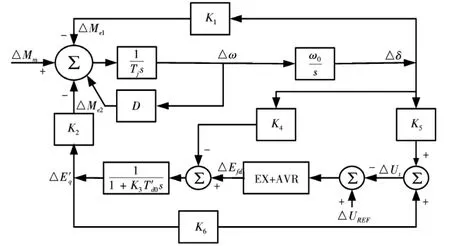
图4 单机无穷大系统的Heffron-Phillips模型

式(11)～(12)中，δ为发电机转子角;ω为发电机转速;Eq为发电机空载电势;E'q为发电机暂态电势;Efd为发电机励磁电势;TJ为发电机惯性常数;D为发电机阻尼系数;T'd0为发电机d轴定子绕组开路下的励磁绕组暂态时间常数;TE为d轴开路暂态时间常数;KE为励磁放大增益;U为无穷大系统电压;Ut为发电机端电压;Pe为发电机输出的电磁功率;X为发电机与无穷大系统间电抗;Xq为发电机q轴同步电抗;Xd为发电机d轴同步电抗;X'd为发电机d轴暂态电抗;Id为发电机q轴电流分量;Id为发电机d轴电流分量。

多机系统的Heffron-Phillips模型与式(11)相同，根据式(11)所示的状态空间，利用模态分析理论求出状态矩阵对应的特征值及左、右特征向量，并找出系统机电振荡模式，根据振荡模式计算系统阻尼比，对弱阻尼比和负阻尼比的机电振荡模式，计算参与因子和相关比，确定PSS的装设地点，利用PSS提供正的附加阻尼力矩，改善系统的阻尼特性。

区域间电网互联规模的进一步扩大，区域间低频振荡已成为危害电网安全稳定运行，限制区域间输电能力的重要因素，PSS受测量信号获取的限制，一般采用本地量测信号作为控制输入，对抑制区域内低频振荡效果显著，而抑制区域间振荡将受量测信号限制，作用有限。利用直流输电系统的功率调制可有效区域间功率振荡，类似于PSS是发电机的稳定控制器，直流的功率调制控制器是系统的稳定控制器。根据直流功率调制的动态过程［19］，结合式(11)和(12)，含HVDC的多机Heffron-Phillips模型表示为:

利用式(13)所示的Heffron-Phillips模型即可分析含HVDC的交直流互联系统小扰动稳定性，然后再根据分析结果借鉴PSS的设计方法可设计HVDC功率调制控制器，改善互联电网的动态稳定性。

3 直流调制参数整定

控制策略的设计是影响直流调制效果的关键因素，常用的调制策略基于控制理论中的根轨迹法［20］。根轨迹设计直流调制控制策略的出发点是，认为加入直流调制后的闭环控制系统具有一对主导共轭极点，交直流互联系统暂态相应特性主要由这一对主导共轭极点的位置决定。通常将系统性能指标的要求化为决定期望主导极点的位置。引入适当的校正装置，利用其零极点改变原系统根轨迹，使校正后系统的根轨迹通过期望主导极点或通过期望主导极点的邻域。

图5 闭环控制系统框图

在交直流互联系统中，以直流输电系统的功率增量△Pdc作为控制变量，交流联络系统有功功率增量△Pac作为被控制变量，并将△Pac作为反馈输入，系统的闭环传递函数框图如图5所示。系统传递函数为:

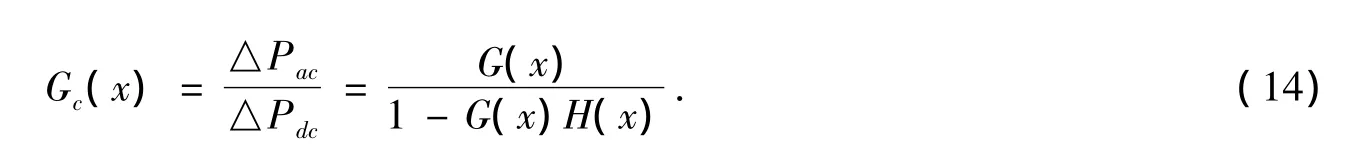
对应的闭环系统特征方程为:

加入反馈环节H(x)后，闭环系统的主导极点为s*，则s*必满足如下条件:

由式(16)便可计算直流调制环节H(x)所需补偿的相位和增益，根据图3可知调制环节利用了3级超前滞后补偿环节。每级补偿arg(H(s*))/3，由超前环节基本公式可知式()中参数α、T分别为:

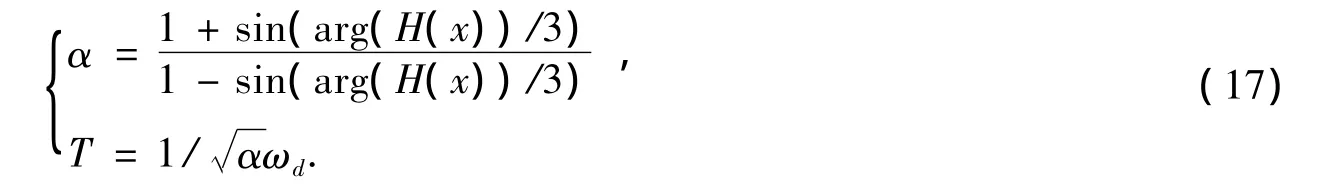
再根据直流附加控制器传递函数Gp(x)等于H(x)的特点，可计算出式(10)的增益KGP:

将α、T、KGP代入式(10)即可得出图3所示的直流附加控制器的各参数。

4 仿真分析

为验证本文提出的直流输电系统功率调制改善电力系统小扰动稳定控制策略，以图6所示的交直流互联系统为例进行仿真分析。该交直流互联系统的具体参数见文献［21］，系统稳态运行时直流联络线和交流联络传输的有功功率分别为200 MW，在该稳态运行点处进行模态分析的结果表明，该系统共有3个机电振荡模式，分别为f1=0.572 Hz，ζ1=0.0069的区域间振荡模式，该模式为发电机1、2逆反与发电机3、4相对运动;f2=1.053 Hz，ζ2=0.071的区域内振荡模式，该模式为发电机1逆反与发电机2相对运动;f3=1.108 Hz，ζ3=0.079的区域内振荡模式，该模式为发电机3逆反与发电机4相对运动。由计算结果可知，区域间振荡模式为弱阻尼模式，需改善该机电模式下的阻尼特性。

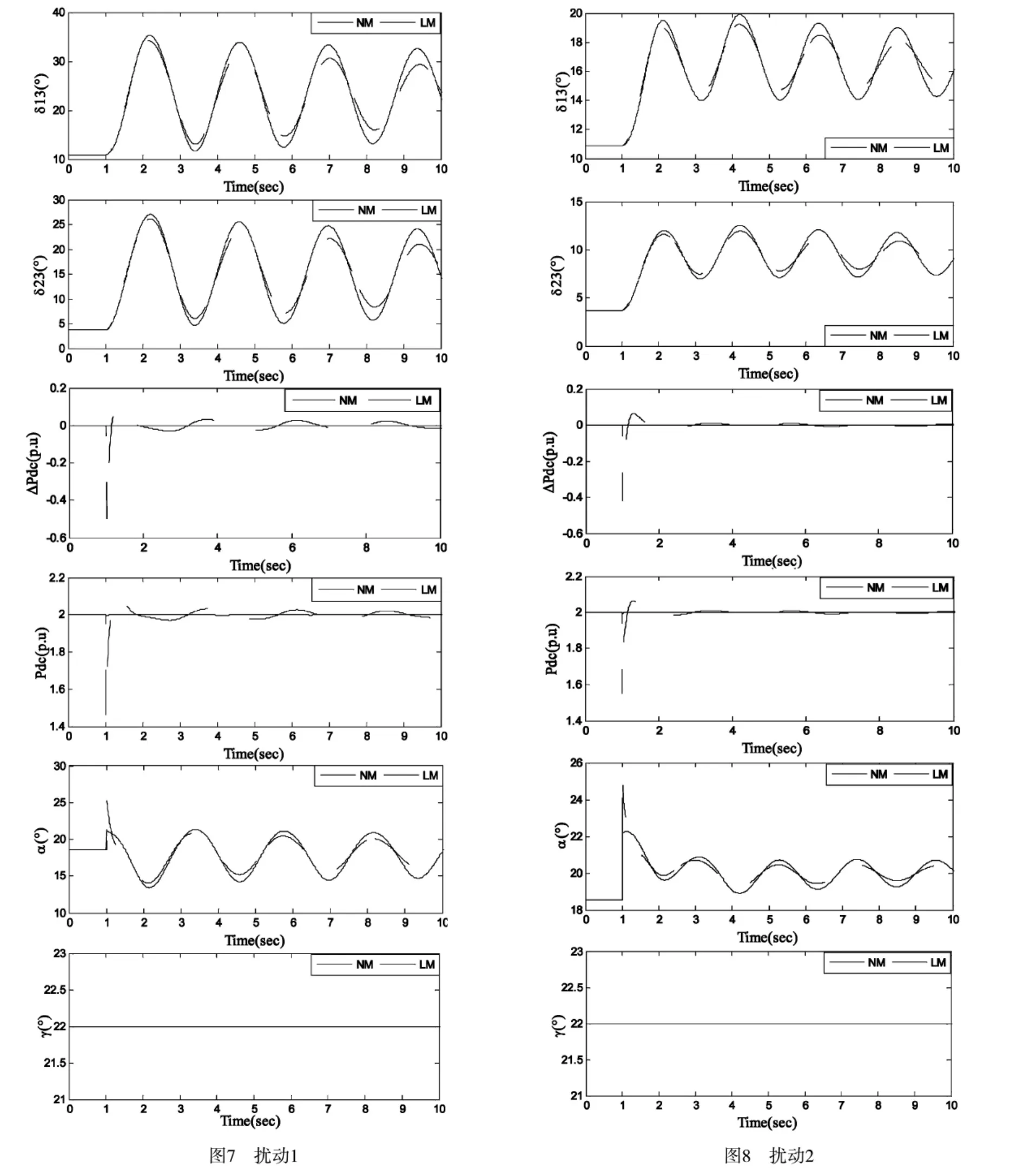
为改善该区域间振荡模式的阻尼特性，采用直流调制的预期目标是将该振荡模式的阻尼比提高到ζ*1=0.2左右。根据计算可知要使期望主导共轭极点为-0.7065±j3.53，需提供的超前补偿相位为 121°，在根据式(16)～(18)对图3所示的直流功率调制环节的参数进行整定。对整定后的参数所形成的式(14)所示的含HVDC的多机Heffron-Phillips线性化模型进行模态分析，结果为:f1=0.512 Hz，ζ1=0.193;f2=1.054 Hz，ζ2=0.073;f3=1.11 Hz，ζ3=0.080。结果表明，采用加入直流调制后，显著提高了区域间振荡的阻尼比，改善了系统的小扰动稳定性，但直流调制对区域内振荡模式影响不大，由此可知，在交直流互联系统中改善区域内振荡模式的阻尼特性易采用PSS;而改善区域间振荡模式的阻尼特性易采用直流调制。为进一步验证直流调制抑制区域间低频振荡的效果本文进行了时域仿真，扰动方式为:扰动1，无故障停运母线7、8间的支路1和母线8、9间的支路1;扰动2，无故障停运母线8、9间的支路1。仿真结果见图7、8。图中，NM表示无直流功率调制;LM表示采用本文的功率调制策略。仿真结果表明，采用直流功率调制可有效抑制系统功率振荡，改善互联系统的动态稳定性。

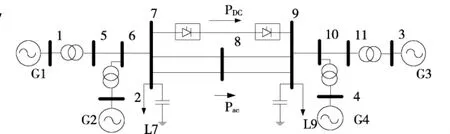
图6 4机交直流互联系统

5 结 论

本文提出并建立了含HVDC的多机Heffron-Phillips线性化模型;通过模态分析理论分析了HVDC阻尼系统功率振荡的机理;利用根轨迹法对直流输电系统功率调制环节的参数进行整定;提出采用PSS抑制区域内振荡和采直流调制抑制区域间振荡相结合地改善系统小扰动稳定性策略。最后以典型交直流互联系统进行仿真分析，模态分析和时域仿真结果表明，基于根轨迹设计的单输入单输出超前—滞后补偿功率调制控制器方法简单、实用、实现容易;直流输电系统本身不具有阻尼功率振荡功能，采用附加控制器后才可有效改善系统的小扰动稳定性;直流输电系统调制可显著改善区域间低频振荡模式的阻尼特性，但对抑制区域内振荡模式效果不佳。

［1］刘振亚.特高压电网［M］.北京:中国经济出版社，2005.

［2］刘振亚，舒印彪，张文亮，等.直流输电系统电压等级序列研究［J］.中国电机工程学报，2008，28(10):1-8.

［3］舒印彪.1000kV交流特高压输电技术的研究与应用［J］.电网技术，2005，29(19):1-6.

［4］舒印彪，张文亮.特高压输电若干关键技术研究［J］.中国电机工程学报，2007，27(31):1-6.

［5］舒印彪，胡毅.交流特高压输电线路关键技术的研究及应用［J］.中国电机工程学报，2007，27(36):1-7.

［6］舒印彪，张文亮，周孝信，等.特高压同步电网安全性评估［J］.中国电机工程学报，2007，27(34):1-6.

［7］郑宝森，郭日彩.中国互联电网的发展［J］.电网技术，2003，27(2):1-3.

［8］余贻鑫，李鹏.大区电网弱互联对互联系统阻尼和动态稳定性的影响［J］.中国电机工程学报，2005，25(11):6-11.

［9］朱芳，赵红光，刘增煌，等.大区电网互联对电力系统动态稳定性的影响［J］.中国电机工程学报，2007，27(1):1-7.

［10］荆勇，洪潮，杨晋柏.直流调制抑制南方电网区域功率振荡的研究［J］.电网技术，2005，29(30):53-56.

［11］M.Klein，G.Rogers，P.Kunder.A Fundamental Study of Inter-Area Oscillations in Power System［J］.IEEE Transactions on Power System，1991，6(3):914 -921.

［12］T.Smed，G.Andersons.Utilizing HVDC to Damp Power Oscillations［J］.IEEE Transactions on Power Delivery，1993，8(2):620 -627.

［13］D.E.Martin，W.K.Wong，D.L.Dickmander，et al.Increasing WSCC Power System Performance with Modulation Controls on the Intermountain Power Project HVDC System［J］.IEEE Transactions on Power Delivery，1992，7(3):1634 -1642.

［14］A.E.Hammad.Stability and Control of HVDC and AC Transmission in Parallel［J］.IEEE Transactions on Power Delivery，1999，14(4):1545-1554.

［15］赵畹君.高压直流输电工程技术［M］.北京:中国电力出版社，2004.

［16］W.G.Heffron.R.A.Phillips.Effect of a Modern Amplidyne Voltage Regulator on Under Excited Operation of Large Turbine Generators［J］.IEEE Transactions on Power Apparatus and Systems，1952，71(1):692 -697.

［17］F.P.deMello，C.Concordia.Concept of Synchronous Machine Stability as Affected by Excitation Control［J］.IEEE Transactions on Power Apparatus and Systems，1969，88(4):316 -329.

［18］M.K.El-Sherbiny，D.M.Mehta.Dynamic System Stability Part I:Investigation of the Effect of Different Loading and Excitation Systems［J］.IEEE Transactions on Power Apparatus and Systems，1973，92(5):1538 -1546.

［19］Y.-X.Ni，V.Vittal，W.Kliema，et al.Nonlinear Model Interaction in HVDC/AC Power Systems with DC Power Modulation［J］.IEEE Transactions on Power Systems，1996，11(4):2011 -2017.

［20］刘取.电力系统稳定性及发电机励磁控制［M］.北京:中国电力出版社，2007.

［21］P.Kunder.Power system stability and control［M］.New York McGraw-Hill，1994.