计及异步风电机组的电力系统区域间ATC计算

李国庆，韩 悦，孙银峰，姜黎莉

(东北电力大学电气工程学院，吉林吉林1320121)

风力发电是当前世界上增长速度最快的新能源利用方式，近年来全球风电市场每年都以超过20%的速度增长［1］。根据国家“十一五”规划，2020年我国风电装机容量将达到30 GW，占全国电力总装机容量的3%。随着越来越多大型风电场直接连入输电系统，有关风电并网的相关研究工作日益得到多数电力研究工作者的重视［2～4］。

可用输电能力(Available Transfer Capability，ATC)［5］直接相关于电力系统的安全稳定运行、系统阻塞的发生及市场参与者对电网使用状况的信息，是十分重要的系统运行参数［7～9］。如何准确地确定电力系统区域间的可用输电能力及其影响因素，使系统在满足安全性及可靠性的条件下，最大限度的满足各区域的用电负荷需求，成为当今电力系统所面临的亟待解决的研究课题。

在含风电场的输电系统中，由于风速的随机性和间歇性直接影响风电场的有功出力和无功吸收，从而对ATC产生不可忽视的影响［11］。关于ATC的模型和计算国内外已经有大量的研究，但考虑风电机组接入电力系统后的ATC的模型及其计算的研究工作还很少，文献［6］提出一种基于序贯蒙特卡罗仿真的风电并网系统ATC评估，这种方法采用时间序列法建立风电场的风速和输出功率的模型，利用序贯蒙特卡罗仿真，综合考虑风电场风速、负荷、发电机出力和设备故障等不确定性因素来进行系统时序状态的抽样，针对大量采样状态的ATC计算。

本文首先考虑滑差为状态变量，且风力机的机械功率和异步发电机转子功率在系统达到稳态时平衡，推导出含风电机组的电力系统潮流模型［11，12］;然后，将含风电机组的潮流模型和传统的静态安全性ATC模型相结合，建立了含风电机组的ATC模型;接着，采用现代内点理论对该模型进行求解;最后，通过仿真计算结果，分析了风电机组接入电力系统后对ATC产生的影响。

1 含风电机组的潮流模型

目前风电场主要使用的风机类型可概括为三类，即定速异步机 (Fixed Speed Induction Generator，FSIG)、同步直驱式风机(Permanent magnetic Synchronous Generator，PMSG)和双馈异步式风机 (Doublyfed Induction Generator，DFIG)［13］。

本文主要对大型定速异步机组风电场接入系统时，对系统可用输电能力产生的影响展开研究。定速异步机风电机组，它吸收风力机提供的机械能，发出有功功率，同时从系统吸收无功功率以提供其建立磁场所需的励磁电流。由于没有电压调节能力，因此不能把它简单地视为电压幅值恒定的PV节点或者功率恒定的PQ节点，必须根据其本身的特点，建立含风电场的潮流模型。这里借鉴文献［12］建立含异步风电机组的潮流计算模型的方法，考虑滑差为状态变量，且风力机的机械功率和异步发电机转子功率在系统达到稳态时平衡，推导含风电机组的ATC计算模型。

1.1 异步风力发电机的稳态数学模型

异步风力发电机在超同步速运行时，转子绕组输出交流电通过变流器馈入电网，此时风力机以发电方式运行，此时吸收风力机提供的机械能，发出有功功率，同时从电网或电容器吸收无功功率提供其建立磁场所需的励磁电流(见图1)，多台风电机组按照一定规则排列构成风电场，风电场的功率为所有风电机组输出功率之和［15］。

由于图1中Xm≥X1，且定子电阻和铁心的功率损耗与有功功率Pe相比可忽略，因此，可以将励磁支路移至电路首端，得到简化的异步发电机Γ型等值电路，如图2所示［16］。在图2所示的简化电路中，可由电路连接关系求出风电机组无功功率和有功功率的表达式:

式中:Xn=X1+X2，U为机端电压。由式(1)可见，当异步发电机输出的有功功率Pe一定时，它吸收的无功功率Qe与机端电压U、滑差s的大小有密切关系。风电机组的原动力是不可控的，风机是否处于发电状态以及出力的大小都取决于风速状况［15］。风力机组的输出功率与其轮毂高度处的风速之间的关系如下:

式中:A是扫风面积;Cp是效率系数;ρ是空气密度［14］。当风速V大于风机的切入风速而且小于额定风速时，按照此公式计算风机的出力;当风速大于额定风速而小于风机的切出风速时，风机功率为其额定功率。

1.2 含风电机组的潮流模型

常规潮流方程为:

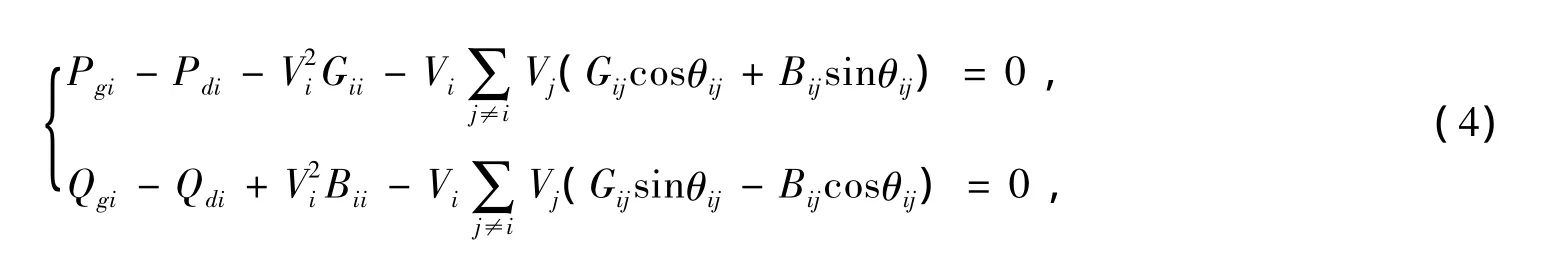
式中，i∈SN，SN为所有节点集合;Pgi和Qgi分别为节点i的发电机有功和无功功率;Pdi和Qdi分别为节点i的负荷有功和无功功率;Vi和θi分别为节点i的电压幅值和相角;Gij+jBij为系统节点导纳阵中的元素［11］。

在计算含风电机组的电力系统潮流时，必须考虑风电机组的数学模型，将系统功率方程和描述风电机组数学模型的方程进行交替迭代求解。由于新增了状态变量s，因此必须增加一组平衡方程。在系统达到稳态时，风力机的机械功率和异步发电机转子功率应该相等，即在原有节点潮流等式约束的基础上，增加风电机组机械功率和电磁功率之差的等式约束:

式中:Pm(k)、Pe(k)分别为第k台风力机的电磁功率和机械功率［15］。由于增加了各台风力机的滑差作为状态变量，那么此时所有变量包括:各台风力机的滑差s、各发电机有功出力PG、各发电机无功出力QG、节点电压幅值U及节点电压相角θ等。当迭代过程中这两个功率不等时，需要修正滑差s，最终使风力机机械功率和发电机电磁功率相平衡。

风电机组一般接在系统中的PQ节点，设节点i为接有风电机组的节点，则节点i对应的潮流方程为:

其他未接入风电机组的节点，其潮流方程仍为常规潮流方程。相应地，潮流方程的雅可比矩阵也要在常规潮流雅可比矩阵的基础上做适当的修正［14～16］。

2 含风电机组的ATC数学模型

含风电机组的ATC数学模型是在传统静态安全性ATC数学模型基础上结合风电机组的潮流模型形成的［17］，修正后的含风电机组的ATC数学模型为:

(1)目标函数

本文将计算IEEE30节点系统(见图3)区域一到区域三间的ATC。那么，目标函数即为:

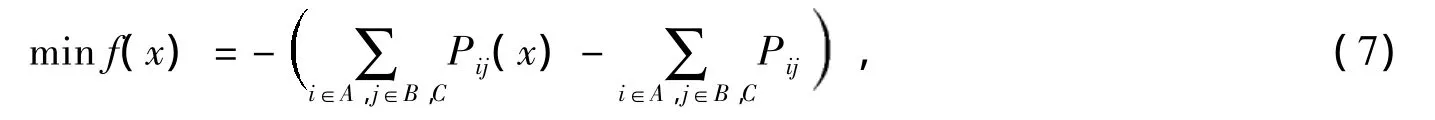
式中:A、B、C分别代表IEEE30节点系统区域一、区域二和区域三，∑Pij为区域一到区域二、三所有联络线上的基态潮流;∑Pij(x)为区域一到区域二、三所有联络线上的现有有功功率;x为系统状态变量和控制变量。将区域二的发电机出力和各节点负荷固定于基态下，并将区域三的发电机出力固定，而在优化中令区域三各节点负荷在其上下限内可调。由于优化算法模型中取最小化，故取两者差值并加负号。

(2)等式约束

等式约束条件即为含风电机组的潮流模型，同式(6)。

(3)不等式约束主要考虑系统有发电机组出力约束、负荷容量约束、无功补偿容量约束、节点电压和线路电流约束，即

式中，Sg是送电区的所有发电机节点集合，Sd是受电区的所有负荷节点集合，Ss装有无功补偿装置的节点集合，SN为系统所有的节点集合;变量上角标*、min、max分别表示基态潮流中的值、变量的下限和上限值［19］。

3 模型求解

将第二节的含风电机组的ATC模型简化为以下非线性优化模型:

这里f(x)为目标函数，g(x)为等式约束，h(x)为不等式约束，x为系统的状态变量和控制变量［19］。引入松弛变量u，l将不等式约束式转化为等式约束:

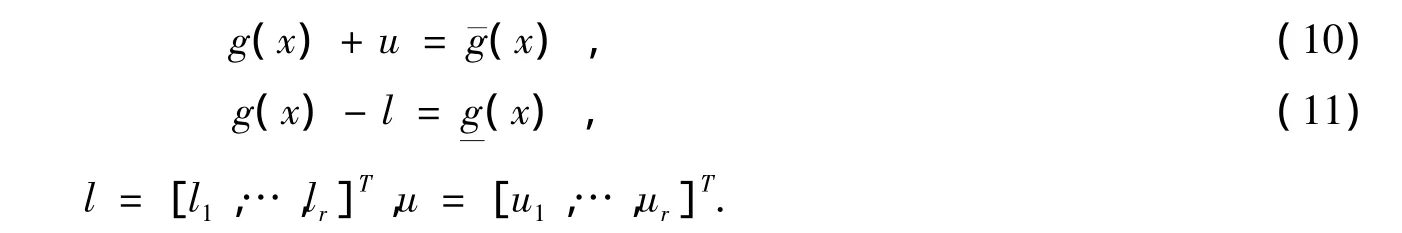
设置障碍常数(或称扰动因子)μ，将目标函数改造为障碍函数。这样，就通过目标函数的变换把含有不等式限制的优化问题变成了只含等式限制的优化问题，因此可以直接用拉格朗日乖子法来求解［20］。

优化后的拉格朗日函数为:

式中上标 ～表示为对偶变量。

根据KKT最值条件，该问题极小值存在的必要条件是拉格朗日函数对所有变量及乘子的偏导数为0［13］:

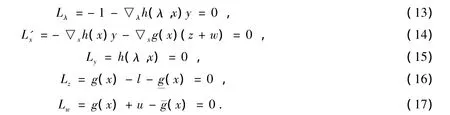
极值的必要条件式(13)～(17)是非线性方程组，经用牛顿拉夫逊法求解后，将式(13)～(17)线性化得到修正矩阵方程:

对变量进行重组和矩阵变换后，算法只需对一个相对较小的对称矩阵进行求解，即:

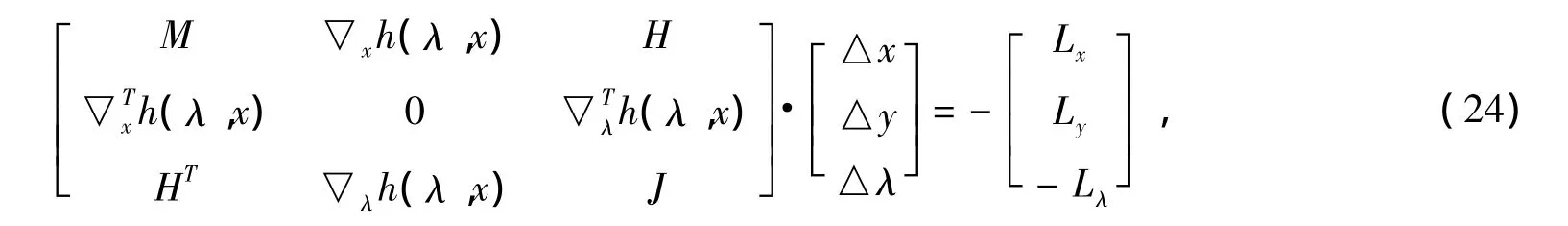
剩余的计算量只是回代。因此，不仅可减少计算量、加快计算速度，同时也简化了算法的编程［17～19］。

解后得到第k次迭代的修正量，于是最优解的一个新的近似为:

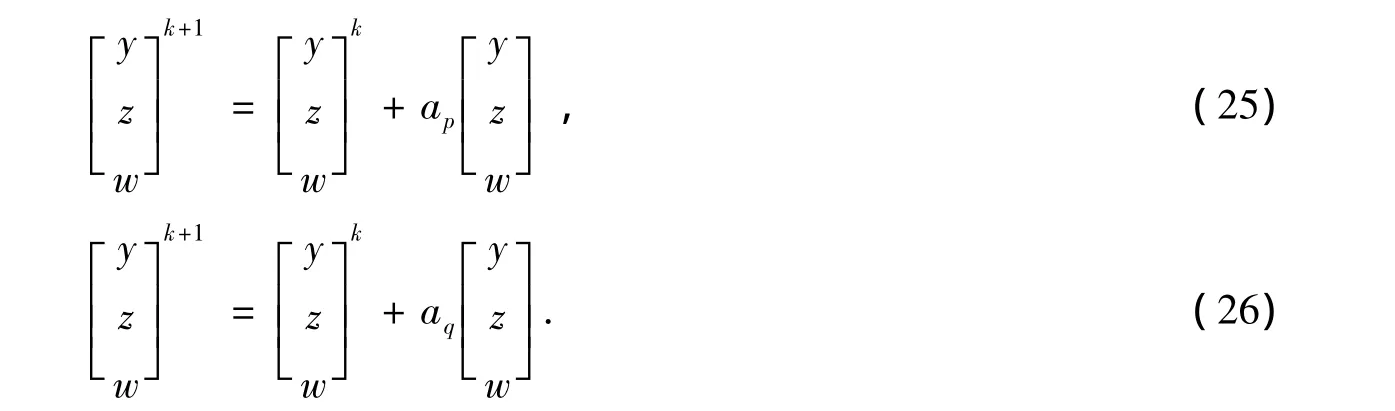
为了保证变量的可行性，最大的原始及对偶步长ap和aq需按下式选取:

i=1，2，…，r0在迭代的过程中，取扰动因子μ为:

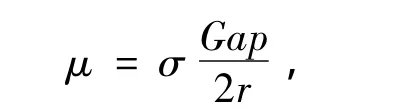
式中:Gap=lTz-uTw称为互补间隙，σ∈(0，1)称为中心参数［15］。

综上所述，该算法计算步骤可总结为:

(1)进行潮流计算将当前的运行点作为初始点:

① 设置松弛变量l，u，保证［l，u］T＞0，

② 设置对偶变量，满足［z＞0，w＜0，y=0］T，

③取中心参数σ∈(0，1)，给定计算精度ε=10-6，迭代次数初值k=0，最大迭代次数Kmax=50;k＜Kmax。

(2)计算互补间隙Gap=lTz-uTw，如果Gap＜ε，则输出最优解，停止计算。

(5)找出原始及对偶变量的最大步长ap和aq。

(6)更新原始、对偶变量。

4 算例分析

为验证所建模型及采用的算法的正确性和有效性，本文在IEEE30节点标准系统上进行仿真计算，如图3所示。该系统共有6台发电机，41条线路，划分为3个区域。限于篇幅，只讨论区域1到区域3的ATC的仿真计算。

本文将10台风力发电机通过升压变压器接到节点4［11］。风力发电机的机端额定电压UN=0.69 kV，单机容量PN=2 MW，风电场地区空气密度为1.2245 kg/m3，风力机的扫掠面积为1840 m2。风力机的切出风速和额定风速分别为20 m/s和14 m/s，定子阻抗0.01+j0.1(p.u.)，激磁电抗Xm=3(p.u.)，转子阻抗0.01+j0.1(p.u.)，滑差取值范围在 -0.0004 到 -0.00898 之间。

图3 含风电机组节点的IEEE30节点系统图

图4为IEEE30节点不含风机节点系统采用内点法计算区域1到区域3的ATC计算数据结果，计算所得ATC值111.08 MW，图5为风电机组接入系统后以风速14 m/s为例的ATC计算结果，计算所得ATC值98.74 MW。

从计算出的ATC数值结果可以看出，风电机组接入系统后，对区域间的可用输电能力会产生不利影响。异步风电机组在发出有功的同时需要从系统吸收大量的无功，若不对含有风电机组的输电系统进行无功补偿，将造成大量无功穿越，将会使整个系统的输送能力降低［1，21］。

另外含风电机组的ATC模型的计算较不含风电机组的ATC模型计算迭代次数增加很多。这是由于含有风电机组的数学模型在静态安全性ATC数学模型的基础上增加了一个新的状态变量，以及一个新的平衡方程。所以在计算过程中还需要对新的ATC模型的雅可比矩阵以及二阶海森阵中的相应元素进行修正。

下面仍以风电场风速14 m/s的情况为例，讨论含风电机组系统采取无功补偿对ATC的影响。含风电机组系统中所装设的无功补偿装置最常用的是机械投切电容器，由于母线1和母线2接有发电机，可作为无功电源，所以只需在母线4，与风电机组接入相关的节点进行无功补偿。节点的无功补偿容量设在-1 Mvar～42 Mvar之间。

表1 IEEE30节点系统不同运行方式下ATC计算结果比较

表1为IEEE30节点系统不含风电机组系统与含有风电机组节点系统以及含有风电机组系统且加入无功补偿装置后的ATC计算结果比较。

计算结果表明:感应异步风电机组在发出有功的所要消耗的大量无功功率，是导致系统ATC值下降的原因之一，若对其进行无功补偿，可以相应提高含风电机组系统的可用输电能力水平。

表2为在几种不同风速下，风电场风电机组的有功无功、滑差以及此时系统区域一到区域三之间的ATC值。

从表2数据可以看出风电场的平均风速决定了风电场能够注入系统的平均功率的大小，风速越高，风电场注入系统的功率越大，从而使系统区域间ATC值随着平均风速的增大而明显增大。而且在风速达到一定值时，由于风电场出力的增大会使系统区域间的ATC值有所提升，或可能高于不含风电机组的水平，这也表明即使增加的是风电场这种波动性的电源，在风速达到一定高速的情况下也能提高该系统的ATC。这就要求系统在风速发生变化时，对风电场所在节点的无功补偿措施进行进一步的规划。

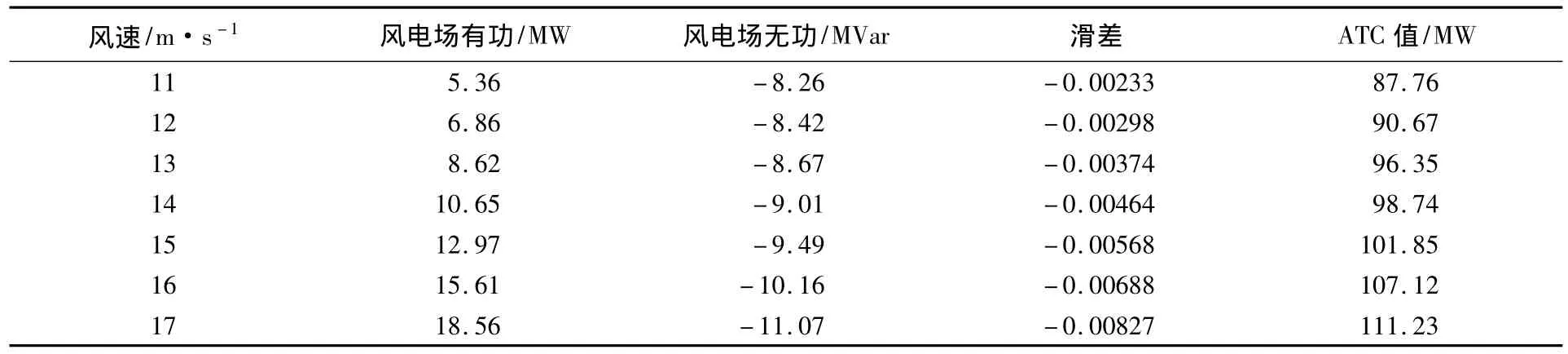
表2 风电场不同风速下的ATC计算结果比较

5 结束语

本文考虑将风电机组接入电力系统中，并借鉴含有风电机组的潮流计算模型，将静态安全ATC模型和含有风电的潮流计算模型相结合。运用现代内点理论对模型进行求解，在求解过程中，对简约修正矩阵中对应元素进行了推导修正，使算法对含风电机组系统的ATC模型的求解更精确有效。通过仿真计算结果分析了风电场对系统区域间可用输电能力的影响，同时也验证了参考的模型和所采用算法的合理性和有效性。

［1］迟永宁，刘燕华，王伟胜，等.风电接入对电力系统的影响［J］.电网技术，2007，31(3):77-81.

［2］陈金富，陈海焱，段献忠.含大型风电场的电力系统多时段动态优化潮流［J］.中国电机工程学报，2006，26(3):31-35.

［3］雷亚洲，王伟胜，印永华，等.含风电场电力系统的有功优化潮流［J］.电网技术，2002，26(6):18-21.

［4］王海超，鲁宗相，周双喜.风电场发电容量可信度研究［J］.中国电机工程学报，2005，25(10):103-106.

［5］NERC.Available transfer capability definition and determination:a reference document prepared by TTC task force［R］.New Jersey:North American Electric Reliability Council，1996.

［6］周明，冉瑞江，李庚银.风电并网系统可用输电能力的评估.中国电机工程学报，2010，30(22):14-21.

［7］李国庆，王成山，余贻鑫.大型互联电力系统区域间功率交换能力研究综述［J］.中国电机工程学报，2001，21(4):20-25.

［8］Ying Xiao，Song Y H.Available transfer capability evaluation by stochasticprogramming［J］.IEEE Power Engineering Review，September 2000，20(9):50 -52.

［9］Kulyos Audomvongseree，Akihiko Yokoyama.Consideration of anappropriate TTC by probabilistic approach［J］.IEEE Trans.on Power Systems，2004，19(1)):375 - 383

［10］Luonan Chen，Asako Ono，Yasuyuki Tada，et al.Optimal operation of power systems constrained by transientstability［J］.Trans.IEEE Japan，2000，120 -B(12):311 -315.

［11］刘春平，童小娇，周任军.含风电机组的ATC的光滑化模型及其有效算法［J］.长沙理工大学学报，2009，6(3):49-53.

［12］王成山，孙玮，王兴刚.含大型风电场的电力系统最大输电能力计算［J］.电力系统自动化，2007，31(2):17-21.

［13］张兴，张龙云，杨淑英，等.风力发电低电压穿越技术综述［J］.电力系统及其自动化学报，2008，20(2):1-8.

［14］王成山，王兴刚，孙玮.含大型风电场的电力系统概率最大输电能力快速计算［J］.中国电机工程学报，2008，28(10):56-62.

［15］顾承红，艾芊.基于改进内点法的含风电场的系统最优潮流计算.中国电力［J］.2007，40(1):89-93.

［16］吴义纯，丁明，张力军.含风电场的电力系统潮流计算［J］.中国电机工程学报，2005，25(4):36-39.

［17］李国庆，赵钰婷，王利猛.计及统一潮流控制器的可用输电能力的计算［J］.中国电机工程学报，2004，24(9):44-49.

［18］王锡凡.现代电力系统分析［M］.北京:科学出版社，2003.

［19］李国庆，姚少伟，陈厚合.基于内点法的交直流混合系统可用输电能力计算.电力系统自动化［J］.2009，33(3):35-45.

［20］李国庆，李雪峰，沈杰，等.牛顿法和内点罚函数法相结合的概率可用功率交换能力计算.中国电机工程学报，2003，23(8):17-22.

［21］吴俊玲，周双喜，孙建锋.并网风力发电场的最大注入功率分析［J］.电网技术，2004，28(20):28-32.