一种确定小扰动稳定域的新算法

李 江，魏丹萍，张忠杰，张少杰，李国庆

(1.东北电力大学电气工程学院，吉林吉林132012;2.上海市电力公司检修公司，上海200072;3.通辽供电公司，内蒙古通辽028000)

小扰动稳定域是指一组稳态运行点的集合，这些稳态运行点本身是小扰动稳定的［1］。文献［2］指出，小扰动稳定域的边界可能包含Hopf分岔(Hopf Bifurcation，HB)、鞍结点分岔(Saddle-Node Bifur Cation，SNB)和奇异诱导分岔 (Singularity Induced Bifurcation，SIB)三种界面。目前对小扰动稳定域边界的研究，有些文献主要关注鞍结分岔［3，4］，有些文献主要关注Hopf分岔［5-7］。这些分岔一般采用平衡点特征根进行分析。然而，近年来已有文献指出，即使系统的特征值实部全部为负，小扰动下非线性特性造成的分岔也会导致系统特性和状态发生突变，产生增幅振荡，造成小扰动不稳定［8］。而传统的特征根方法无法分析这些非线性环节，因此这就需要采用新方法进行分析。

电力系统在实际运行过程中遇到的非线性环节众多，例如功率约束、电压约束、各种开关的动作和控制器的饱和环节等都可能产生非线性问题，其中控制器的饱和环节就是一类关键的非线性环节。受到物理结构的限制，实际系统的控制输入总是要求在一个安全范围之内，这在模型中体现为饱和环节。在电力系统稳定研究中，一些学者发现发电机励磁系统饱和环节的存在与混沌现象及电压崩溃有关［9，10］。然而，当计及饱和环节后特征根方法将无法分析这种非线性环节。文献［11］指出，计及饱和环节的线性化系统存在吸引域，同时给出了基于矩阵不等式计算吸引域的新方法。本文基于文献［11］的饱和系统吸引域计算方法，针对线性最优励磁控制(LOEC)下的多机系统，提出了基于吸引域体积为指标确定小扰动稳定域边界的新方法。

1 传统控制下小扰动稳定域边界的确定

动态电力系统可写为

式中，x为动态状态变量，如发电机的功角、角速度等;y为代数状态变量，如网络潮流计算的节点电压幅值、相角等;p为控制参数变量，如节点负荷、控制器增益、时间常数等;f为描述发电机转子运动方程、电磁暂态过程、励磁调节器动态过程等的非线性方程组;g为网络的潮流代数方程组。

其中，Jsys为动态系统的雅可比矩阵。随着参数p的变化，当系统发生Hopf分岔时，动态系统的雅可比矩阵有一对实部为零的共轭纯虚特征根;当系统发生鞍结分岔时，动态系统的雅可比矩阵有实特征根穿过虚轴;当系统发生奇异诱导分岔时，▽yg奇异。系统的小扰动稳定域Ω可定义为［9］

因此，小扰动稳定域的边界∂Ω由上述三类分岔点的闭包组成，即:

为保守获得小扰动稳定域，可用如下算法实现［5］:

算法1

(1)选择构造稳定域的参数空间，假定系统中的其它参数不变;

(2)确定参数空间中一个小扰动稳定的运行平衡点，作为搜索稳定域边界的初始点;

(3)在参数空间中，从初始点起沿某一射线方向，以一定的步长准静态的改变参数变量，得到一系列新的系统平衡点，并对每一个平衡点计算动态系统的雅可比矩阵特征值;

(4)当系统出现一对共轭纯虚特征值且其余特征值均有负实部时，系统发生Hopf分岔，记录此时的参数，该点即为小扰动稳定域的边界点;

(5)改变步骤(3)中搜索边界点所用的射线方向，重复(3)和(4)，得到新的边界点。

这种在参数空间(p1，p2)中，逐点搜索小扰动稳定域边界点的方法虽然计算量较大，但具有较好的准确性和灵活性。

2 LOEC下小扰动稳定域边界的确定

通过动态方程的线性化，采用LOEC控制的系统可表示为［12］

式中，A∈Rn×n为系统矩阵;B∈Rn×r为输入矩阵;△x∈Rn×l为系统状态变量;u∈Rr×n为系统控制变量。若系统(4)能控，利用文献［12］提出的方法设计状态反馈增益F，则控制变量u=F△x，系统(4)的闭环系统可表示为

对系统(5)，若系统(4)能控，方程(5)可解，反馈增益存在。但是，受到实际系统的限制，反馈增益矩阵的各元素不能太大。需设定最大、最小反馈增益值，本文取F的元素fij≤200。当反馈增益大于最大反馈增益值时，反馈增益元素fij=200;当反馈增益小于最小反馈增益值时，反馈增益元素fij=-200。通过改变控制参数，计算系统各个运行点的最优励磁控制增益。由于受最大最小反馈增益值的约束，系统(5)可能存在Hopf分岔，即小扰动稳定域的边界。根据这一思想，可计算线性LOEC控制下的小扰动稳定域边界，形成如下新算法:

算法2

(1)～(2)与算法1相同;

(3)在参数空间中，从初始点起沿某一射线方向，以一定的步长准静态的改变参数变量，得到新的系统平衡点，并求解线性化方程对应的代数Riccati方程，进一步获得反馈增益矩阵。若fij大于最大反馈增益值，fij=200;否则继续;

(4)～(5)与算法1的步骤(4)～(5)相同。

该算法与算法1都是通过Hopf分岔确定小扰动稳定域的边界，具有与算法1相同的优点。

3 饱和系统小扰动稳定域边界的确定

实际运行的系统中控制变量u不可能无限大，其必然在一个安全范围内。若采用状态反馈控制，Fi为反馈增益矩阵F∈Rm×n的第i个行向量，可定义饱和函数

其中，fsati(Fi△x)(i=1，…，m)为

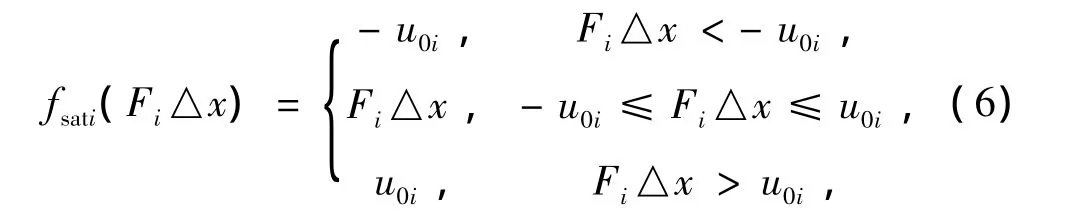
其中，u0i为励磁顶值，其关系也可用图1直观表示。

若计及饱和环节，控制律u=fsat(F△x)，则闭环线性系统为

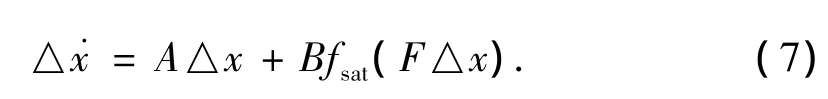
为获得系统(7)的椭球吸引域可用如下定理:

定理1［13］对系统(4)，若控制输入u有界，u0i=ri，i=1，…，m，满足饱和函数(6)的最大椭球吸引域 ε(Q-1，1)可通过求解以Q∈Rn×n，S=diag(s1，…，sm)，为变量的下列凸优化问题得到:

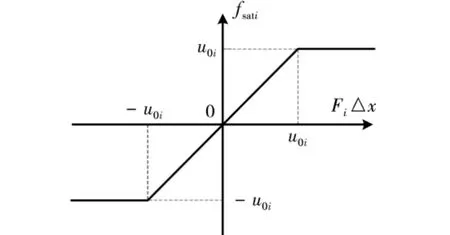
图1 饱和环节的非线性特性

式中，Ar=A+BTrF，Bpr=BRr，Tr=diag(ρ1，…，ρm)，Rr=diag(δ1，…，δm)，ρi=1/2(1+1/ri)，δi=1/2(1 - 1/ri)，i=1，…，m。

式(8)的优化问题可以借助于文献［14］介绍的MAXDET软件实现求取的椭球吸引域最大化。由于在式(3)表示的小扰动稳定域内部不会发生Hopf分岔、鞍结分岔和奇异诱导分岔，因此使用矩阵不等式方法计算饱和系统的椭球吸引域时，式(8)可能有解也可能无解。若有解则说明该运行点计及饱和环节后是小扰动稳定的;若无解则说明系统计及饱和环节后是小扰动不稳定的。根据这一思想，形成如下算法:

算法3

(1)～(2)与算法1中(1)～(2)相同;

(3)在参数空间中，从初始点起沿某一射线方向，以一定的步长准静态的改变参数变量，得到新的系统平衡点，根据式(8)计算饱和系统的椭球吸引域。当椭球吸引域不存在或过小，系统小扰动不稳定，该点即为小扰动稳定域的边界点;

(4)与算法1中(5)相同。

在使用过程中，当不考虑扰动大小时，算法3中的椭球吸引域体积指标可以取较小的值;当考虑扰动大小时，算法3中的椭球吸引域体积指标可取较大值。因此，与算法1和2相比，算法3具有更大的灵活性，并且能够提供更多元的信息。

4 算例分析

算例采用WSCC-3机9节点系统，其模型见附录［15］。励磁系统采用标准的IEEEDC1A模型，负荷采用恒阻抗模型，选取发电机G2、G3的有功功率P2、P3作为注入空间的参数变量，利用算法1获得图2所示的小扰动稳定域边界点。同理，利用算法2获得图3所示的小扰动稳定域边界点。对比图2和图3可知，最优励磁控制下的小扰动稳定域ΩLOEC要明显大于传统励磁控制(DC1A模型)下的小扰动稳定域ΩDC1A。

算法3的步骤(3)中，以椭球体的体积作为判断椭球吸引域大小的指标，取临界点体积指标为Vcr=0.005，励磁顶值u0i=5，射线共100条(即射线将单位圆平分为100等份)，获得的小扰动稳定域Ω*如图4所示。从图4中可见，算法3采用凸优化方法获得的小扰动稳定域与算法2获得的小扰动稳定域差别不大，从而验证了算法3的有效性。

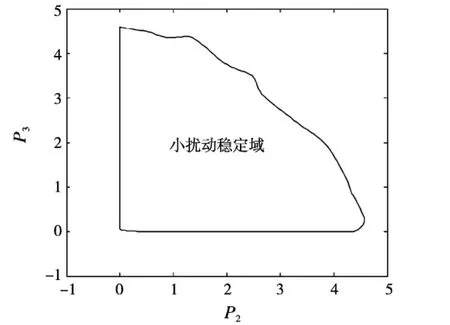
图4 采用新算法确定的小扰动稳定域Ω*

5 结 论

发电机励磁系统的饱和环节是实际系统的现实约束，本文在计及饱和环节后对小扰动稳定域进行了深入研究，提出了以椭球吸引域体积为指标确定小扰动稳定域边界的新算法，算例研究表明采用凸优化方法求取小扰动稳定域是可行的，并且励磁系统采用最优励磁控制的小扰动稳定域要明显大于传统励磁控制(IEEE DC1A模型)方式下的小扰动稳定域，从而也验证了最优励磁控制的优越性。

附 录

电力系统中，多机系统的数学模型可表示为:

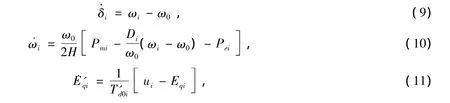
代数方程为

其中，i=1，2，…，n，n为发电机的台数，各参数的意义见文献［15］。

式(9)～(14)，对图5所示的WSCC系统在运行点附近进行线性化，模型可写为

其中，

图5 WSCC系统图

式中，k△E'qi，k△δi，k△ωi，i=1，2，3，分别为 △E'qi，△δi，△ωi的控制器状态增益，增益值可利用文献［15］提出的设计方法设计，R取单位矩阵，Q=［50 10 5 50 10 5 50 10 5］。式(15)满足式(4)、(8)的形式，可用于算法2、3 中。

［1］余贻鑫，王成山.电力系统稳定性理论与方法［M］.北京:科学出版社.1999.

［2］贾宏杰.电力系统小扰动稳定域的研究［D］.天津:天津大学.2001.

［3］Dobsoni，LU L.Computing an optimum direction in control space to avoid saddle node bifurcation and voltage collapse in electrical power systems［J］.IEEE Transactions on Power Systems，1992，37(10):1616 -1620.

［4］Alvarado F，Dobson I，HU Y.Computation of closest bifurcation in power systems［J］.IEEE Transactions on Power Systems，1994，9(2):918 -928.

［5］孙强.电力系统小扰动稳定域及低频振荡［D］.天津:天津大学.2007.

［6］Alvarado F L.Bifurcations in nonlinear systems:computational issues［C］.Proceedings of ISCAS Conference，May 1 -3，1990，New Orleans，LA，USA.

［7］Hill D.Nonlinear computation and control for small disturbance stability［C］.Proceedings of IEEE Summer meeting，July 16 -20，2000，Seattle，WA，USA.

［8］Chin-Woo T，Varghese M，Varaiya P，et al.Bifurcation，chaos，and voltage collapse in power systems［J］.Proceedings of the IEEE，1995，83(11):1484-1496

［9］贾宏杰，余贻鑫，王成山.考虑励磁顶值与PSS的混沌和分岔现象［J］.电力系统自动化，2001，25(1):11-14.

［10］Crow M L，Ayyagari J.The effect of excitation limits on voltage stability［J］.IEEE Transactions on Circuits and System-I Fundamental Theory and Applications，1995，42(12):1022 -1026.

［11］李江，李国庆，李筱婧.计及饱和环节的励磁系统吸引域研究［J］.中国电机工程学报，2010，30(9):111-115.

［12］卢强，王仲鸿，韩英铎.输电系统最优控制［M］.北京:科学出版社，1982.

［13］HINDI H，BOYD S.Analysis of linear systems with saturation using convex optimization［C］.Proceedings of the 37th IEEE Conference on Decision and Control，December 16 -18，1998，Tampa，USA.

［14］Wu S P，Vandenberghe L，Boyd S.Maxdet:software for determinant maximization problems-User’s Guide［J］.1996(5):1 -12.

［15］Anderson P M，Fouad A A.Power system control and stability［M］.New Jersey，USA:IEEE Press，1994.