基于邻域拓扑文化差分进化算法的无功优化模型研究
杨 悦,袁 超,李国庆
(1.东北电力大学电气工程学院,吉林吉林132012;2.中国石油吉林石化公司动力一厂,吉林吉林132022)
随着电力技术的发展,电网规模日益扩大。如何在满足电力用户需求前提下,充分发挥系统无功调节作用,改善系统电能质量,提高系统安全经济运行水平,一直是国内外电力工作者关注的热点问题。通过系统无功优化不仅使全网电压运行在额定值附近,而且还可取得可观经济效益,使电能质量、系统安全经济有效结合,因而研究系统无功优化具有重要实际意义。
无功优化问题一直受到是国内外学者的关注。文献[1]采用二进制编码遗传算法,控制前向反馈人工神经网络的学习进程,进而对电网运行做出优化决策,结果表明所建立的模型是有效的[1]。文献[2]采用整数编码遗传算法搜索电网中负荷分配的最优策略,所设计的算法模型被用来测试实际系统,并借助试验得出了电网负荷不足时该模型能较好地对有限负荷进行最优分配的结论。文献[3]应用遗传算法,求解兼顾降低网损和抑制谐波的配电系统的优化运行问题,一个18节点电网的算例结果表明了求解方法的有效性。余文献[4]提出了结合灵敏度分析的GA,归纳了电网容性无功和感性无功的补偿原则。文献[5]考虑电力系统运行的实际情况,对GA的编码、繁殖、自适应函数以及收敛判据等进行了改进,并提出了GA用于电力系统无功优化中尚存在的问题。目前,对于“双优化、双促进”机制的文化差分进化算法的研究很多,文化差分进化算法是将差分进化算法引入到文化算法的框架,通过文化算法中文化信念的提取及对种群的影响来提高差分进化算法的搜索速度和搜索精度。但普通的文化差分进化算法存在着发生过早收敛,易于陷入局部最优的问题。
综上所述,本文将邻域拓扑的概念纳入了文化进化差分算法,将考虑邻域拓扑结构的文化差分进化算法应用到求解无功优化问题中,通过对IEEE30标准试验系统的仿真计算和分析,结果表明本文提出的算法在求解电力系统无功优化时改进了文化差分进化算法过早收敛,在加速迭代的同时摆脱了易于陷入局部最优解的问题,对求解大规模电力系统无功优化问题将有重要的意义[6]。
1 无功优化的数学模型
电力系统的无功优化目的,采用合适的电容补偿和调节变压器分接头等措施改善系统电能质量,减小网损。其数学模型包括功率约束方程(潮流方程)、变量约束条件和目标函数。
1.1 目标函数
经典的无功优化数学模型的目标函数是以系统的网损最小为目标,但考虑到状态变量越界,即节点电压越界和发电机无功越界问题,本文采用的目标函数中,将节点电压越限及发电机无功出力越限以罚函数的方式进行处理。具体数学模型[7]描述为:

式中,等式右端第一项Ploss为系统网损值;等式右端第二项为对节点电压幅值越限的惩罚项;第三项为对发电机无功出力越限的惩罚项;第四项为对支路电流越限的惩罚项。其中α为系统节点的集合;λV为对节点电压越限进行惩罚的罚因子;β为系统中发电机节点的集合;λG为对发电机无功越限进行惩罚的罚因子;χ为系统支路的集合;λB为对支路电流越限进行惩罚的惩罚因子。惩罚项具体的计算如式(2)-式(4)所示。

1.2 功率约束方程
考虑各节点有功和无功平衡的约束,即

式中,Ui,Uj分别为节点i,j的电压;PGi,PLi分别为节点的发电机有功出力和有功负荷;QGi,QCi,QLi分别为节点的发电机无功出力,容性无功补偿容量和无功负荷;Gij,Bij分别为节点i,j之间的电导和电纳;δij为节点i,j的电压相角差;N为系统节点数。
1.3 变量约束条件
变量约束包括控制变量约束和状态变量约束。无功补偿电源输出Ql和可调变压器分接头位置Tk都受到运行条件和设备本身条件的限制,这些限制构成了控制变量约束。各节点的电压幅值Ui、发电机无功输出QGs、支路电流Ib也会受到各种限制,这些限制便构成了状态变量约束。
控制变量约束有:

状态变量约束有:

式中,Qlmin,Qlmax,Tkmin,Tkmax,Ulmin,Ulmax,QGsmin,QGsmax,Ibmin,Ibmax分别为对应变量的最小值和最大值。
2 基于邻域拓扑的文化差分进化算法
2.1 文化差分算法
2.1.1 文化算法
文化算法(Culture Agorithm,CA)是一个多进化过程算法,可以将文化进化过程看作在两个层面上进行:微观层面和宏观层面之间相互交互、共同合作的继承系统。微观层面演化发生在种群空间(Population Space),利用进化算法对个体进行迭代求解形成知识信息;宏观层面演化发生在在信念空间(Belief Space),保存上述个体知识信息,形成群体经验,并通过与微观层面的交流,对微观层面的后续个体进行迭代指导。种群空间和信念空间是两个相对独立的进化进程,两个空间根据一定的通讯协议(接受函数Accept(),影响函数Influence)来互相联系[8]。在信念空间,知识根据更新函数Update()进行更新,形成群体经验;在种群空间,迭代函数Generate()根据个体行为规则和父辈个体参数生成下一代个体,应用目标函数Objective()来评价空间中个体适应度值,应用选择函数Select()从新生成个体中选择一部分个体作为下代个体的父辈。文化算法的框架如图1所示。
2.2.2 差分进化算法
差分进化算法(Differential Evolution Algorithm,DEA)是由NP(种群规模)个个体矢量j(j=1,2,…,NP),其中每个个体矢量又由n(决策变量个数)维变量xij(i=1,2,…,n;j=1,2,…,NP)组成的种群在搜索空间进行并行直接的搜索以此来求得最优解的算法。它从某一随机产生的初始群体开始,通过把种群中两个个体的矢量差加权,并按照一定的规则产生新个体,然后进行选择,确定下一代新个体。以此方法引导搜索过程,向最优解逼近[9]。Storn和Price不仅提出了DE算法的标准形式,还提出了多种DE算法的变化形式。本文应用的是DE/target-to-best/1/bin形式。该算法涉及的三种基本差分操作如下:
(1)变异操作,变异操作过程如式(12):

图1 文化算法框架
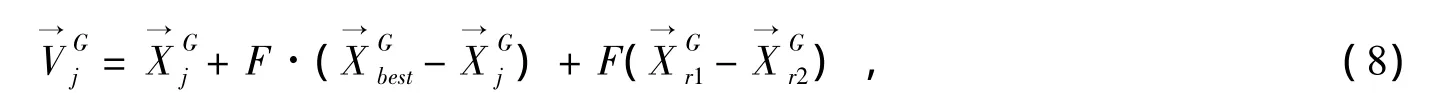


(3)选择操作,即将试验个体与目标个体进行比较,取适应度最优的个体作为下一次迭代的父代。
2.2.3 文化差分进化算法
文化差分进化算法(Cultural Differential Evolution Algorithm,CDEA)的基本思想是用差分进化算法作为文化算法的种群空间,并通过Accept()使种群空间的知识影响信念空间中所存储的知识,并将信念空间的知识进行更新,再应用Influence()来控制差分进化算法的变异、交叉、和选择来指导种群空间的迭代过程。
2.3 文化差分进化算法的改进
2.3.1 邻域拓扑结构


图2 DE/target-to-best/1算法的环形拓扑结构
2.3.2 基于邻域拓扑的文化差分进化算法
文化差分进化算法(Cultural Differential Evolution Algorithm,CDEA)的基本思想是用差分进化算法作为文化算法的种群空间,并通过Accept()使种群空间的知识影响信念空间中所存储的知识,并将信念空间的知识进行更新,再应用Influence()来控制差分进化算法的变异、交叉、和选择来指导种群空间的迭代过程[12]。本文提出在影响函数设计时考虑环形邻域拓扑的影响,加强整体寻优的能力。本文提出的基于邻域拓扑的文化差分进化算法的无功优化建模主要是影响函数的设计,详见文章3.3部分,改进了一般文化差分进化
算法的影响函数,使其可以进行环形邻域的拓展。算法流程图,见图3。
3 无功优化模型的实现

图3 基于邻域拓扑的文化差分进化算法流程图
根据无功优化的数学模型,设种群空间中种群的规模为NP,控制变量的个数为n,G为迭代次数,Gmax为最大迭代次数,实现过程如下。
3.1 接受函数的设计
信念空间中知识的形成和更新并不是对所有个体进行统计而得到的,而是按一定的概率从种群中选取最优秀的个体群作为研究对象,而接受函数正是用来在种群空间中选择直接影响当前信念空间知识形成的个体[13]。种群空间通过接受函数,将个体经验传递到信念空间,实际上是向信念空间提供当代


3.2 信念空间的设计
信念空间的知识是由种群空间的个体经验由接受函数传递到信念空间后形成的。Saleem和Reynolds定义了五种信念空间的知识:规范化知识、形势知识、领域知识、历史知识、拓扑知识。本文介应用规范化知识和形势知识[14]。
(1)规范化知识N[n]



(2)形式知识S
形势知识指保存在信念空间的一组由历代种群产生的最优个体集合,是能够引导其它个体趋近最优的标准[16]。形势知识的数据结构如表1所示。
表1中的第二行是历代种群中的最优个体,第一行是其分别对应的适应度值。初始化形势知识时,取初始种群中的最优个体。形势知识的更新规则如式(15)所示:

表1 形式知识的数据结构

3.3 影响函数设计
(1)基于规范化知识和形式知识影响的变异操作影响函数设计
根据信仰空间更新后的知识,将种群空间中个体的各个变量进行更新,更新规则如式(13)所示。
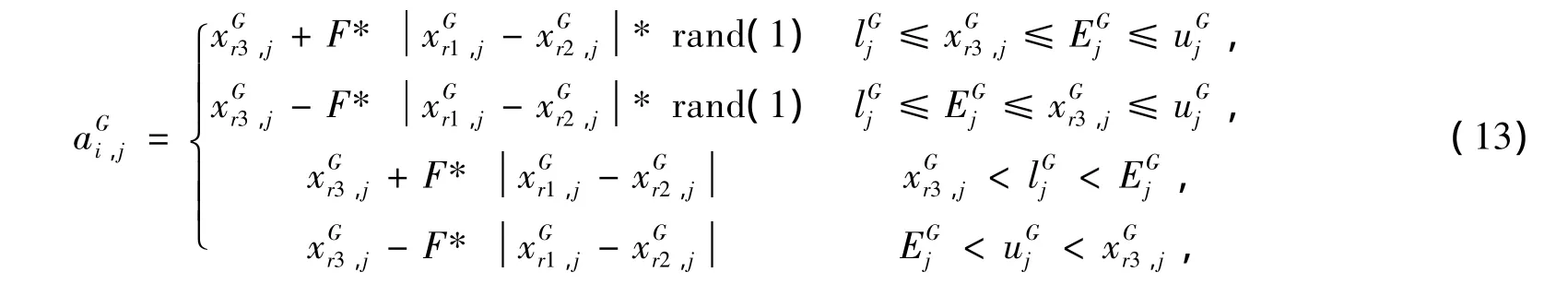
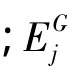
(2)考虑邻域拓扑的变异操作影响函数设计于种群中的每一个个体矢量,都要产生一个局部贡献矢量。这个矢量由它的邻域最好个体矢量和邻域中任意的两个个体矢量的差分量生成,模型如式(14)所示。
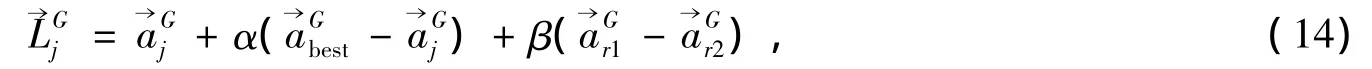


显然,如果¯ω=1且α=β=F,变异矢量就与应用DE/Target-to-Best/1算法生成的变异矢量完全相同,这充分说明了考虑了邻域拓扑后的DE/Target-to-Best/1算法是更具一般性的差分进化算法。¯ω的确定采用的是线性增加法,增加的方法如式(17)所示。

(3)交叉操作的影响函数设计
为增加干扰,使个体矢量具有多样性,引入交叉操作。则实验矢量由变异矢量和目标矢量交叉生成,其各个分量按式(18)计算。

式中,ηi=rand(1),是针对第i维分量随机选择的控制参数;交叉因子CR∈(0,1)为算法参数,需要事先确定[18]。它控制着种群的多样性,帮助算法从局部最优解中脱离出来。
(4)选择操作的影响函数设计
差分进化算法采用的是一种“贪婪”选择模式:当且仅当新个体的评价函数值更好时,才被保留到下一代群体中;否则,父代个体仍然保留在种群体中,再一次作为下一代的父矢量,选择方法如式(19)。
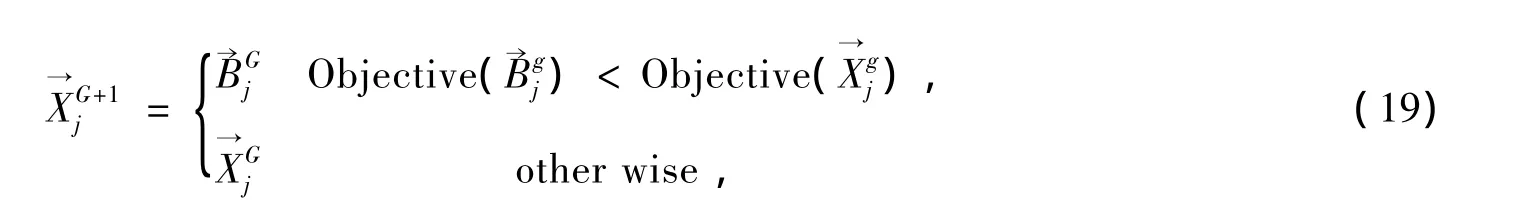
3.4 种群空间的设计
父代根据设计的影响函数在种群空间中进行迭代,以此实现了算法的连续性。
4 实例计算与结果分析
本文以IEEE30节点系统为例验证所建无功优化模型及算法的合理性和可行性,该系统中包括6台发电机,其中节点1为平衡节点,其它节点为PV节点,4台可调变压器,3个无功补偿电容器节点;共有13个控制变量,以网损最小为目标函数,进行仿真计算[19]。本文应用了基于邻域拓扑文化差分进化算法和普通文化差分进化算法分别进行了无功优化计算。两种算法均取群体规模为50,两个比例因子都为0.8,交叉因子为0.80,最大迭代次数为200。由于两种算法使用的都是随机概率搜索技术,因此本文对这两种算法都做了50次计算,取每种方法统计结果的50次平均值。两种算法的统计后的优化结果见表2。图4为两种算法随着迭代次数增加的收敛趋势图。经分析发现,两种算法都能使系统所有节点电压幅值Ui、发电机无功输出QGi电流Ib约束条件。其中,节点电压幅值优化前后大小如图5所示。但从表2、图4和图5可以综合看出,基于邻域拓扑文化差分进化算法的性能优于普通文化差分进化算法的性能。
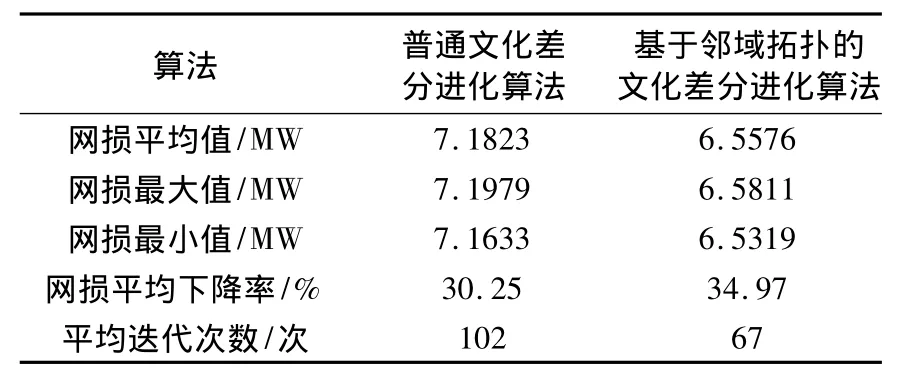
表2 两种算法的优化结果统计

5 结 论
本文提出了一种新基于邻域拓扑的文化差分进化算法,应用邻域拓扑的概念改进了文化进化差分算法,并建立了基于该算法的无功优化模型和流程图,并采用对IEEE-30测试系统进行仿真分析。仿真结果表明,本文提出的改进文化差分进化算法在求解电力系统无功优化时,改进了普通文化差分进化算法过早收敛的问题,同时在迭代过程中易跳出局部最优,增强该算法在无功优化中的全局寻优能力,对求解大规模电力系统无功优化问题具有一定的借鉴意义。
[1]Arjona D,Lay R,Harring ton R.A hybrid artificial neural network/genetic algorithm approach to on-line switching operations for the optimization of electrical power systems[C].Proceeding s of the 31st Inter society Energy Conversion Engineering Conference,1996,4(4):2286-2290.
[2]Luan W,Irving M,Daniel J.Genetic algorithm for supply rest oration and optimal load shedding in power system distribution networks[J].IEE Proceedings-Generation,Transmission and Distribution,2002,49(2):145 -151.
[3]赵勇,韩春立,李建华,等.兼顾降低网损和抑制谐波要求的配电系统优化运行[J].中国电机工程学报,2003,23(1):6-10.
[4]余健明,杜刚,姚李孝.结合灵敏度分析的遗传算法应用于配电网无功补偿优化规划[J].电网技术,2002,26(7):46-49.
[5]张正凯,盛四清,田文树.基于改进遗传算法的地区电网无功优化[J].电力科学与工程,2005(1):73-75.
[6]吴英,金从友等.基于文化算法的电力系统无功优化研究[J].现代电力,2008,25(3):36-41.
[7]任震,钟红梅等.电网无功优化的改进遗传算法[J].电力自动化设备,2002,22(8):16-19.
[8]Robert R G.An Introduction to Cultural Algorithms[C].Proc.of the 3th Annual Conf.on Evolution Programming.Singapore:World Scientific Publishing,1994:131 -136.
[9]Storn R,Price K.Differential evolution:a simple and efficient adaptive scheme for global optimization over continuous spaces[R].Berkeley:University of California,2006.
[10]杜欢.邻域拓扑粒子群优化算法及其在电力系统无功优化中的应用研究[D].杭州:浙江大学,2006.
[11]Swagatam Das,Ajith Abraham et al.Differential Evolution Using a Neighborhood-Based Mutation Operator[J].IEEE Transactions on evolutionary computation,2009,13(3):526 -553.
[12]Ricardo Landa Becerra,Carlos A Coello Coello.A cultural algorithm with differential evolution to solve constrained optimization problems[J].Lecture Notes in Computer Science,2004,3315:881 -891.
[13]黄海燕,顾幸生.文化差分进化算法及其在化工过程建模中的应用[J].化工学报,2009,60(3):668-674.
[14]Reynolds R G,Zhu Shinin.Knowledge-based function optimization using fuzzy cultural algorithms with evolutionary programming[J].IEEE Transactions on Systems,Man,and Cybernetics,Part B:Cybernetics,2001,31(1):1 -18.
[15]Yan W,Lu S,Yu D C.A novel optimal reactive power dispatch method based on an improved Hybrid evolutionary programming technique[J].IEEE Trans on Power Systems,2004,19(2):913 -918.
[16]崔文同,胡春平,颜学峰.基于文化差分进化算法的最小二乘支持向量机及QSAR建模[J].华东理工大学学报(自然科学版),2010,36(1):121 -125.
[17]Storn R,Price K.Differential evolution:a simple and efficient adaptive scheme for global optimization over continuous spaces[R].Berkeley:University of California,2006(1):1 -18.
[18]刘自发,闫景信等.基于改进微分进化算法的电力系统无功优化[J].电网技术,2007,31(18):68-72.
[19]Yan W,Lu S,Yu D C.A novel optimal reactive power dispatch method based on an improved Hybrid evolutionary programming technique[J].IEEE Trans on Power Systems,2004,19(2):913 -918.

